
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Лобачевского и Римана 4 page
|
|
Здесь М - масса планеты, G - гравитационная «постоянная», F - сила взаимодействия с эфирным пространством или с другими телами, е - заряд планеты.
Кеплеровские инварианты обусловливают возможность получение законов физики даже без вывода, простым приравниванием соответствующих из них. Так, например, получаем закон притяжения Ньютона:
R22F/M = M1G; F = GMM1/R22,
Или закон Кулона:
R22F/M =e2/M; F = e2/R22. И т.д.
И можно полагать, что именно инвариантные взаимосвязи параметров лежат в основе всех физических уравнений.
Фундаментальный вывод о пропорциональном изменении всех свойств любой области околосолнечного пространства следует уже из признания вещественности космического пространства. Его можно проверить для Солнечной системы на примере инварианта Тv3 - const1 (2.13), и определить изменяется ли и каким образом скорость течения времени, при «падении» (частный случай - движение планеты по орбите) тела в любой области Солнечной системы.
Понятно, что с приближением к Солнцу период Т будет уменьшаться, поскольку орбитальная скорость движения планеты возрастает, а с удалением от нее увеличиваться. Однако, как постулируется в классической механике, само по себе течение времени в каждой точке пространства остается неизменным и, следовательно, промежутки течения времени в каждой области пространства равны между собой, и по нашему земному времени измеряются секундами. А это означает, что они не должны быть связаны в инварианте нелинейной зависимостью. До сих пор постулат постоянства скорости течения времени в пространстве остается основой любой механической или физической картины мира, поскольку отсутствуют способы его теоретической проверки.
Хотя сам по себе факт изменения скорости вращения планет с приближением к Солнцу тривиален, неизвестен его другой аспект: пропорционально ли изменению скорости вращения планеты вокруг Солнца меняется скорость течения времени. (Неизменна ли, как постулируется, скорость течения времени во всем пространстве Солнечной системы или она меняется от области к области?) И движутся ли тела к Солнцу с возрастающим ускорением? Последнее из наблюдений для всех настолько очевидно, что подобный вопрос кажется нонсенсом. Но наблюдаемое ускорение еще не является доказательством падения тел на Солнце с возрастанием скорости, поскольку нам неизвестно главное - изменяется или нет скорость течения времени в том пространстве, в котором тело приближается к Солнцу? Инвариантность уравнений (2.13), (2.14) свидетельствует о том, что скорость падения тел и скорость течения времени на орбите меняются нелинейно, и обусловливают возможность проведения теоретической проверки постулата о постоянстве течения времени в различных областях пространства.
Для проведения расчетов можно использовать комплекс инвариантов (2.13). Выберем условный шаг измерителя расстояния 12,5 млн. км по радиусу, а за точку начала отсчета примем расстояние от орбиты Земли, тогда S = 9,4×1013 см - длина орбиты, v = 29,78×105 см/с - средняя скорость движения планеты по орбите, а Т = 3,156×107 с - годовое время движения. Расчет будем вести последовательно по инвариантам:
Sv2 = 8,339×1026 см3/с2 - сonst1,
Тv3 = 8,339×1026 см3/с2 - сonst1, (2.20)
и записывать результаты расчета в таблицу 1.
Та б лица 1
| S см 1011 | T сек 104 | V см/c 105 |
| 1. 940,0 | 29,78 | |
| 2. 863,9 | 31,06 | |
| З. 785,4 | 32,58 | |
| 4. 706,8 | 34,34 | |
| 5. 628,3 | 36,42 | |
| 6. 549,8 | 38,94 | |
| 7. 471,2 | 42,06 | |
| 8. 392,7 | 852,5 | 46,07 |
| 9. 314,2 | 609,9 | 51,51 |
| 10. 235,6 | 396,1 | 59,48 |
| 11. 157,1 | 215,7 | 72,84 |
| 12. 78,54 | 76,29 | 103,0 |
| 13. 6,283 | 1,725 | 364,2 |
Итоги оказались весьма неожиданными. Выяснилось, что, с приближением к поверхности Солнца, скорость течения времени в каждой области пространства, не является const. Одновременно с возрастанием скорости падения тел, происходит замедление скорости течения времени в пространстве их движения, и настолько значительное, что если скорость падения на отрезке 149 млн. км возросла на один порядок, то скорость течения времени на этом же отрезке пространства замедлилась более чем на два порядка. И, следовательно, впроцессе орбитального движения тел происходит не ускорение, а по мере их приближения к Солнечной поверхности фактическое значительно более быстрое замедление скорости падения тел в пространстве Солнечной системы. Это и есть та самая мина замедленного действия, которая, если не удастся ее опровергнуть, способна перевернуть все сложившиеся представления о структуре космического пространства в целом, а Солнечной системы в частности. Именно изменяемость скорости течения времени, как и других свойств в различных областях пространства, и скрывал третий закон Кеплера.
Вернемся к уравнению (2.20). Оно - инвариант, произведение параметров годового периода времени на куб средней скорости. Иначе говоря, перед нами уравнение кубической гиперболы, отображающее зависимость изменения орбитальной скорости движения планеты (или любого твердого тела на орбите) от скорости течения времени в той области пространства, в которой находится планета. Для анализа закономерности изменения скорости и времени «вырежем» из таблицы 1 промежуток траектории по длине радиуса от 16 млн. км до 1 млн. км, и рассмотрим подробнее связь структуры изменения расстояния до центра Солнца R, с возрастанием скорости «падения» тела v и замедления течения времени Тпр. Рассчитаем эти параметры с шагом 2 млн. км по инварианту (2.13):
Тпр v3 - const,
и выпишем проявившуюся зависимость в таблицу 2.
Т аблиц а 2
| V см/c. | 3,641×107:2 = | 1,820×107:2 = | 0,910×107: 2 = | 0,455×107: 2 = | … ® |
| R см. | 1×1011 х 4 = | 4×1011 х 4 = | 16×1011 х 4 = | 64×1011 х 4 = | … ® |
| T с. | 1,73×104 х 8 = | 1,38×105 х 8 = | 1,106×106 х 8 = | 8,83×106 х 8 = | … ® |
Вот здесь-то и обнаружится то, что не было заметно по таблице 1. Каждый из параметров изменяется с пошаговой кратностью, как бы квантованностью, равной:
Для скорости падения - двум,
Для расстояния по радиусу (как и по орбите) - четырем,
Для времени падения - восьми.
Из нее следует, что возрастание скорости v падения тела на Солнце происходит в четыре раза медленнее, чем соответствующее замедление течения времени Тпр на том же отрезке траектории. (Другими словами по мере приближения к Солнцу возрастающая плотность пространства, а вместе с ней и напряженность гравитационного поля g, вызывают соответствующее изменение скорости течения времени, что и отображает, например, инвариант g3Т4 – const1.) Поэтому, по мере приближения к Солнцу время областей пространства, в котором движется тело, замедляется в каждой ее области на строго определенную количественную величину, а скорость его движения тоже возрастает на строго определенную, но другую количественную величину в той же области. Характер изменения скорости движения падающего тела и скорости течения времени хорошо отображен на графике (рис. 35.). И как видно из таблицы 2 и на графике замедление падения происходит намного быстрее, чем возрастание скорости тела. Поэтому в каждый последующий промежуток времени тело-планета, приближаясь к Солнцу, будет проходить путь по длине на строго определенную величину меньший, чем за предыдущий промежуток времени. Отсюда следует, что тело «упавшее» на Солнце, не сможет достичь его центра за бесконечный промежуток времени (если исходить из того, что Солнце является газовым шаром и не принимать во внимание сопротивления газа движению тела).
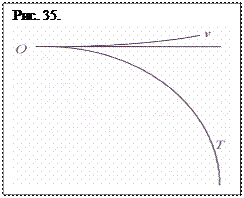 Как видно на графике, замедление времени Т падения тела происходит намного быстрее возрастания скорости v тела. И в каждый последующий промежуток времени тело − планета, приближаясь к Солнцу, проходит путь по длине меньший, чем за предыдущий промежуток времени. Следовательно, тело, “упавшее” на Солнце, не сможет достичь его центра за бесконечный промежуток времени.
Как видно на графике, замедление времени Т падения тела происходит намного быстрее возрастания скорости v тела. И в каждый последующий промежуток времени тело − планета, приближаясь к Солнцу, проходит путь по длине меньший, чем за предыдущий промежуток времени. Следовательно, тело, “упавшее” на Солнце, не сможет достичь его центра за бесконечный промежуток времени.
Повторимся:
Геометрическое пространство появляется только тогда, когда имеет место явное или неявное механическое движение фигур. В статических геометриях пространство отсутствует, поскольку отсутствует взаимодействие фигур с пространством.
Известно, что точка-тело, в движении которой вдоль прямой на бесконечности каждый последующий шаг оказывается меньше предыдущего, на строго нормированную величину, не сможет пройти ограниченный отрезок линии даже за бесконечный промежуток времени. Именно эта ситуация и наблюдается при рассмотрении процесса падения тел на Солнце по комплексу уравнений (2.13). Поскольку тела на Солнце могут падать с любой стороны и в своем падении замедляются на строго определенный отрезок расстояния, то ни один из них не в состоянии достичь его центра, а, следовательно, их траектория нигде не пересекаются.
Это обстоятельство, обусловленное движением падающих в пространстве тел, показывает, что аксиома о динамических параллельных не является аксиомой, а есть следствие третьего закона Кеплера. Есть отображение теоретического вывода о том, что тела падают на Солнце с отрицательным ускорением (с замедлением). И эта констатация могла появиться только после того, как удалось выяснить теоретически замедление скорости свободного падения тел по мере их приближения к Солнцу.
Выводы из анализа третьего закона Кеплера:
Движение точек-тел полудинамической геометрии по эллиптическим траекториям описывается третьим законом Кеплера.
Закон Кеплера не ограничивается констатацией равенства отношений квадратов периодов к кубам расстояний, а сопровождается системой инвариантов, отображающих изменение параметров тел и пространства при движении.
Согласно инвариантам Кеплера, скорость течения времени пространства по мере приближения к Солнцу замедляется, а падающие тела деформируются возрастающей напряженностью его гравиполя.
Можно полагать, что аппарат динамической геометрии является математическим инвариантным аппаратом физики.
2.9. Строение физического
пространства
Известно, что проблема бесконечного включает дихотомию взаимосвязи двух пар категорий, с одной стороны, различие конечного и бесконечного, с другой - покоя и движения. Попарно существование противоположных категорий обусловливает различие в подходе к описательному отображению космических тел и структур. Это различие прежде всего относится к первичным понятиям: тело-точка, прямая-луч, плоскость, движение, время и т.д.
Простейшее тело в динамической геометрии можно представить как материальную сферу, бесконечную внутрь и отграниченную собственной поверхностью от окружающего пространства. Тело, как вещественное образование, формирует плотностную структуру и влияет на внешнее пространство в соответствии с энергетической напряженностью, создаваемой количественной величиной своих свойств.
Тело можно представить точкой только тогда, когда ее параметры и собственная напряженность несопоставимы по рангу с параметрами и напряженностью окружающего пространства и тел, образующих структуру данного пространства.
Линия или прямая есть условный след от движения точки (тела) в пространстве. И начало, и конец линии входят в поверхность «динамических» точек. Линия, на участке от поверхности одной точки-сферы до поверхности другой, имеет конечную длину.
Если эту же прямую продолжить за пределы поверхности конечных точек-сфер, внутрь их, то прямая станет иметь бесконечную длину, не отождествляемую ни с какими действительными числами.
Вернемся к бесконечной прямойна плоскости и точке N вне ее, через которую проводится прямая. Это плотностная точка и аналогичную плотностную функцию имеет ближайшая к N точка М на «бесконечной» прямой. Они взаимодействуя “создают” поле напряженности (штрихи нарис. 26), и для них, как уже говорилось, отсутствует прямая АВ на которой находится М. Именно движение прямой через точку N, «сопровождаемое» неявным движением точки М вдоль прямой АВ становится фактором определяющим истинную форму образуемых параллельных.
Образующий луч Л (рис. 26) в природе отсутствует. Он - фигурное отображение факта силового взаимодействия между центрами и соединяет плотностные точки, которые в своем движении, “выписывают” различные как плоские, так и объемные фигуры. Это как бы изменяемая ось греческой колесницы.
Неявное существование образующего луча создает возможность в статико-динамической геометрии обобщения геометрий Евклида, Лобачевского и Римана в одной и той же области пространства простым “замораживанием" отдельных линий (или всех). Последнее свидетельствует о том, что полудинамические и статические геометрии являются производными элементами динамической геометрии.
В пространственных полудинамических системах образующий луч Л всегда подвижен, и каждая его концевая точка в процессе движения описывает геометрическую фигуру, соответствующую уравнению движения и коэффициенту связности. Естественно, что в уравнении движения зашифрована и напряженность области концевых точек луча и пространства, в котором луч движется. (Везде предполагается, что след движения остается только от перемещения концевых точек.)
Основной способ движения образующего луча - собственное удлинение или сокращение (пульсация) с определенным периодом, сочетающийся с возможным вращением и некоторым пространственным перемещением, например в пространстве декартовых координат. Поэтому кривые (следы), плоскости и пространства всех геометрий, включая геометрии Евклида, Лобачевского и Римана, описываются образующим лучом, один конец которого может двигаться по линии или оставаться неподвижным, а другой, в движении, удлиняться или сокращаться. На рис. 36 показано, как, двигаясь на плоскости, образующий АО от точки А до точки А', остается неизменным по длине и описывает дугу окружности полностью в соответствии с геометрией Евклида. В точке А' он в движении начинает укорачиваться и до точки А" движется по сферической кривой, описывая линию положительной кривизны в соответствии с геометрией Римана. В точке А " происходит следующий перелом и образующий на участке А" А"' начинает описывать линию отрицательной кривизны по геометрии Лобачевского до точки А"', после которой линия движения снова меняет «свою» геометрию и т.д. Переломные точки А', А", А "¢, А"" имеют статическую для этой области величину луча, и потому луч в них может быть отнесен к геометрии Евклида. Перелом есть изменение формального качества линии, процесс перехода от одной кривизны к другой.
| Рис. 36. А ¢ Л А ¢¢ Л А ¢ Л М Л А¢¢¢ |
Оба конца луча могут совершать любые движения, описывать самые различные фигуры. Так, например, если конец луча, описывающий кривую AA'A"A'"... (см. рис. 36), замкнется при одновременном движении другого конца-точки О по прямой, то выписывается объемная фигура - профилированный цилиндр. Если же точка О будет двигаться по окружности, то вместо цилиндра получается тор того же профиля. Таким образом, возникновение искривления как «положительного», так и «отрицательного», связано с изменением длины луча, создающего это «искривление». Длина луча, в свою очередь, зависит от напряженности пространства в различных направлениях от точки, из которой он исходит. Изменение напряженности не есть искривление поверхности и не приводит к нему, а вызывает изменение метричности. И, следовательно, численной длины луча. Покажем это на примере (рис. 37). Пусть луч AО, исходящий из условной точки О, двигаясь по отрезку окружности АВО, начал удлиняться и в точке А' пересек прямую А"О. Продолжая дальнейшее движение, он пересек также прямую ОВ" - окончание дуги АВ.
Дуга АВ разделена прямыми на четыре равных отрезка k, 1, т, п. Прямые, разделившие дугу, продолжены до пересечения эквипотенциальной линии А" В" и также делят эту дугу на четыре равных отрезка k", l¢¢, т", п". В пространстве отрезки
k" = k= l¢¢ = 1 = т" = т = п" = п,
как следствие пропорционального изменения напряженности от точки О к периферии поверхности. Поскольку пропорциональность 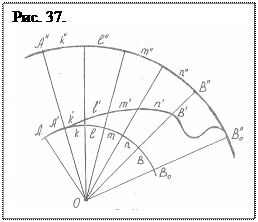 напряженности сохраняется на всей поверхности, то отрезок А'В' делится на четыре части k ¢, l ¢, т', п', так что:
напряженности сохраняется на всей поверхности, то отрезок А'В' делится на четыре части k ¢, l ¢, т', п', так что:
k' = l¢ = m' = п',
хотя по евклидовой и римановой геометрии k' ¹ п'.
Естественно также, что
k = k ¢ = k ¢¢; l = l ¢ = l"; m = m' = m"; п = п' = п".
То есть все отрезки физически равны между собой так, что отношение каждого из отрезков к длине соответствующего луча между эквипотен-циальными дугами будет величиной постоянной. Именно это свойство напряженности пространства обусловливает образование пространственных ячеек - основных элементов динамической геометрии. Напряженность и изменение метричности (кривизна относительно статичности) - это те факторы, которые не учитывались в теории кривизны ни Гауссом, ни Риманом. Отметим, что, похоже, кривизны поверхностей, а тем более кривизны объемов в пространстве не существует. А поскольку геометрическое пространство отображает динамическую структуру реального мира, то эмпирическое подтверждение ее адекватности этому миру можно получить на поверхности Земли.
Приведем описание нескольких экспериментов, подтверждающих такую возможность. В долине вблизи гор можно построить горизонтальную мерную милю из идеального материала длиной в 3 км (с точностью до 1 см). Произвести геодезическую съемку этой мили и перенести ее размеры теодолитом на горное плато на высоту одного, а лучше 2 км, и там построить другую горизонтальную мерную милю той же длины. Современные геодезические приборы позволяют провести операцию переноса размеров на несколько десятков километров с точностью до 1-2 см. В соответствии с геометрией Евклида мили и в долине и на плато должны быть равной длины. Однако миля на плато на высоте 1 км будет на 47 см длиннее мили в долине, а на высоте 2 км - на 94 см.
Следует замерить милю в долине несколькими металлическими мерными линейками, проведя ими же в аналогичных условиях измерение мили на плато, убедиться, что она в точности, до ошибок измерения, равна миле в долине, а следовательно, мерные линейки изменили свою длину.
Другой эксперимент: на горе с горизонтальным плато на высоте 2 км выложить горизонтально из 40-50 стальных стержней длиной по 20-25 м (± 0,1 мм) единый стержень километровой длины. Отметки его концов перенести теодолитом в долину под горой, потом разобрать конструкцию, перебросить ее в долину и вновь собрать. Согласно геометрии Евклида собранная конструкция будет длиннее отметок на 32 см. Однако стержни при измерении метром окажутся в рамках отметок ± ошибка измерения.
Наконец можно просто провести геодезическими приборами измерение отрезка относительно горизонтальной поверхности в долине на длине 10 км и, замерив такую же длину, перенесенную на плато на высоту 2 км, убедиться с достаточно грубым приближением (± 25-30 см) в появлении при измерении отрезка почти трехметровой длины. (Можно предположить, что аналогичные нестыковки уже встречались картографам и геодезистам но не получали объяснения.)
Рассмотрим в общих чертах структуру пространственной ячейки отграниченной нейтральными зонами. Пространственные первичные ячейки, соизмеримые по напряженности с напряженностью окружающего пространства, образуются ядрами по периметру своей нейтральной зоны. В настоящей работе напряженность схематически обозначается условной линией, как бы оставляемой ядром тела, взаимодействующего с пространством и другим телом. Эти линии по наглядности являются некоторым подобием фарадеевых силовых линий, а в геометрии это геодезические линии.
Прямые напряженности выходят из пространства одного ядра 1 (рис. 38) с фиктивным центром О 1 и входят в пространство другого ядра 2 с фиктивным центром О 2. Линии напряженности О 1 АО 2, О 1 ВО 2, О 1 СО 2..., соединяющие фиктивные центры, в пространстве параллельны. В точках А, В, С, D,... они испытывают кажущееся преломление, обусловленное зоной единой минимальной напряженности - нейтральной или эквипотенциальной зоной.
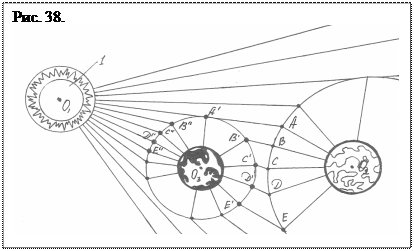 Ячейка, например, О3 образуется только тогда, когда оба ядра имеют пространственную линию общей эквипотенциальной зоны (нейтральные зоны), как бы выделяющую их из окружающего пространства. Эти зоны образует для них единую систему, не позволяют ядрам покинуть ее. Именно ячейки обусловливают дискретность пространства одного ранга.
Ячейка, например, О3 образуется только тогда, когда оба ядра имеют пространственную линию общей эквипотенциальной зоны (нейтральные зоны), как бы выделяющую их из окружающего пространства. Эти зоны образует для них единую систему, не позволяют ядрам покинуть ее. Именно ячейки обусловливают дискретность пространства одного ранга.
Первичные ячейки через нейтральные зоны взаимодействуют с окружающими ячейками и входят в состав ячеек несоизмеримого ранга. Общая структура пространства - иерархия равенства. В пространстве ячейки между ядром и нейтральной зоной могут существовать спутники ядра 3 с центром О 3. Между спутником и ядром также существует нейтральная зона А' В' С'... А"В"С", охватывающая спутник эллиптической сферой. Выходящие из центра O 1 линии входят в центр О 3 или замыкаются в нейтральной зоне. Радиус (статический) спутника определяется граничными условиями. Пространство ячейки, ядра и спутника всегда находятся в движении.
Ядро как элемент ячейки и самостоятельная система единой внутренней напряженности имеет сложную структуру, обусловленную материальностью самого образования. Оно включает несколько «скорлуп»-сателлитов 1 (рис. 39.), у которых нейтральная зона 2 каждой скорлупы находится либо внутри этой поверхности,
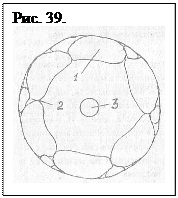 либо у самой поверхности, что и удерживает их в единой системе. Поэтому сферы сателлитов, взаимодействуя нейтральными зонами, образуют на своей внешней поверхности равновеликую напряженность, интегрированную уже как напряженность самого ядра. Пространство (рис. 39.) внутри скорлуп материально и имеет напряженность более высокого ранга, чем снаружи. В этом пространстве может находиться внутреннее вещественное ядро-керн 3. Его напряженность несоизмерима по рангу ни с напряженностью пространства ячейки, ни с напряженностью сателлитов. Она есть плотность другого ранга.
либо у самой поверхности, что и удерживает их в единой системе. Поэтому сферы сателлитов, взаимодействуя нейтральными зонами, образуют на своей внешней поверхности равновеликую напряженность, интегрированную уже как напряженность самого ядра. Пространство (рис. 39.) внутри скорлуп материально и имеет напряженность более высокого ранга, чем снаружи. В этом пространстве может находиться внутреннее вещественное ядро-керн 3. Его напряженность несоизмерима по рангу ни с напряженностью пространства ячейки, ни с напряженностью сателлитов. Она есть плотность другого ранга.
Выводы:
Геометрическое пространство появляется только тогда, когда имеет место явное или неявное механическое движение точек-тел. В статических геометриях пространство отсутствует, поскольку отсутствует взаимодействие фигур с пространством.
Уравнения, описывающие движущиеся в пространстве точки, “создают” между ними неявную зону изменяемой плотности (аналогию анизотропного пространства).
Движущиеся в пространстве на бесконечность точки “взаимодействуют” между собой по прямой - образующей.
2.10. Свойства пространственных систем
Рассмотрим, что неявно происходит с пространством при возникновении в нем тел, отображаемых элементами динамической геометрии. Возьмем чистый лист бумаги и предположим, что этот лист есть некоторая плоскость, однородная и изотропная в обоих направлениях, а, следовательно, на пространстве листа мы не замечаем никакой структуры и внутренней напряженности. Эта поверхность может быть названа бесформенной, хаотичной, или поверхностью одного ранга. Структура этого ранга и его ячейки нами не фиксируются.
Поставим в любом месте листа точку. Точка на листе никакой роли не играет, структуры не создает, и как бы не возникает напряженности различной плотности на всей поверхности. Но хаос уже исчез, точка становится центром образования нового пространства, центром структуризации и изменения его качеств, центром другого ранга. И не существенно, пространство ли это листа или пространство космоса, в котором имеется тело. Существенно в подходе к явлению, к его формализации - другое. Образует ли точка пространство актуальной бесконечности или бесконечности потенциальной? Именно одна из сторон двойственности обусловливает процесс понимания формализации элементов различных пространств по мере их воссоздания на листе.
Точка, как и другие элементы в пространстве потенциальной бесконечности (или в объеме), не равнозначна другим, не видимым на листе точкам, и уже создает (даже если это не отражают условия задачи) в окружающем пространстве некоторую напряженность, определяемую изменением метричности пространства. Именно метричность есть агент, отображающий распространение плотности напряженности от точки в пространстве. При этом на бесконечности одного ранга плотность убывает от точки до нуля. (Нулевая плотность напряженности равна напряженности, создаваемой телами нижнего ранга и потому не равна 0.) Поскольку значимость точки определяется ее рангом и рангом пространства, то ранги определяют также изменение метричности.
Если на плоскости (в пространстве) имеется две или несколько точек, то напряженность между ними определяется рангом точек. Поскольку в задачах чаще всего задается одинаковый ранг, то плотность напряженности между точками становится неоднозначной. Но между ними всегда имеется зона одинаковой плотности напряженности - нейтральная зона. Структура всех напряженностей между точками определяется именно характером и местом нейтральных зон. В плоскости (как и в объеме) актуальной бесконечности напряженность отсутствует, а, следовательно, может отсутствовать и метричность (что и наблюдается в проективной геометрии). Если же она как бы присутствует, то неизменна величиной по всей плоскости (по всему объему), и точка, как и другие фигуры в этом пространстве, на пространство никакого влияния не оказывает.
Поставим еще одну точку. Структуризация возросла. Между точками по различным критериям может быть найдена активная область или нейтральная зона, разделяющая как их, так и плоскость листа. Или они могут быть соединены одной линией, которая делит лист уже на две иные, чем нейтральная линия, части, создавая иные пространства по обе ее стороны.
Соединим точки линией и в одном из образовавшихся пространств, в стороне от линии поставим точку, создав тем самым все необходимые предпосылки для формулирования или пятой аксиомы Евклида или основной аксиомы динамики пространства. Все имеющиеся на плоскости элементы равнозначны или, по современной артикуляции, равноправны, и только движение определяет их принадлежность к динамике. Если теперь со стороны прямой, восстановив до точки М образующий луч, двигать его неизменным по длине вдоль прямой, то точка, в которую он вошел, будет оставлять след евклидовой прямой, параллельной базовой. И это будет продолжаться бесконечно, если... если мы не последуем за Дезаргом. Дезарг, исходя из кажущегося пересечения в перспективе параллельных в одной точке, предложил считать пересечения проекциями «бесконечно удаленных» точек, равноправными со всеми остальными элементами. Так в проективную геометрию вошли «несобственные (бесконечно удаленные) точки» и «несобственные плоскости» - плоскости, на которых лежат эти точки.
Введение «несобственных» точек и плоскостей нарушило равнозначность элементов геометрии, было первым качественным отображением на плоскости факторов напряженности пространства и свидетельствовало о другом ранге несобственных точек. Однако нарушения равнозначности элементов обнаружено не было, и не потому, что оно отсутствует, а потому, что и обычным, и несобственным точкам и площадям постулировали равноправие. Это постулирование равноправия обусловило полную статичность проективной геометрии, снивилировало напряженности, привело к тому, что все прямые одной плоскости Дезарга всегда пересекаются на бесконечности. Таким образом, вопрос о различной напряженности у точек и линий на плоскости даже не возник. Развитие получили аксиомы статической геометрии.
Date: 2015-04-23; view: 673; Нарушение авторских прав