Способ прямоугольного треугольника. Определение натуральной величины отрезка прямой линии и углов наклона прямой к плоскостям проекций

Построение проекций отрезка прямой общего и частного положения позволяет решать не только позиционные задачи (расположение относительно плоскостей проекций), но и метрические – определение длины отрезка и углов наклона к плоскостям проекций. Но эта задача может быть решена только в случае, если отрезок параллелен или перпендикулярен к одной или нескольким плоскостям. Рассмотрим способ решения такой задачи для отрезка общего положения.

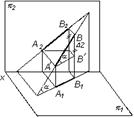
Пусть дан отрезок АВ общего положения относительно плоскостей p₁ и p₂. АВ'В – прямоугольный треугольник (рис. 3.10), в котором катет АВ' = А₁В₁ (проекции отрезка АВ на плоскость p₁), а катет ВВ' равен z – разности расстояний точек А и В до плоскости p₁. Угол a в прямоугольном треугольнике АВ'В определяет угол наклона прямой АВ к плоскости p₁.

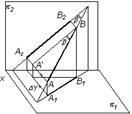
Рассмотрим треугольник ВА'А (рис. 3.11), где катет ВА' равен проекции А₂В₂ (ВА' = А₂В₂), а второй катет АА' равен D y – разности расстояний точек А и В от плоскости p ₂. Угол 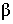в прямоугольном треугольнике ВАА' определяет угол наклона прямой АВ к плоскости p₂.

Таким образом, натуральная длина отрезка прямой общего положения определяется гипотенузой прямоугольного треугольника, у которого один катет равен проекции отрезка, а второй катет – алгебраической разности расстояний от концов отрезка до одной из плоскостей проекций.

Рис. 3.10	Рис. 3.11

14 Определение видимости прямых относительно плоскостей проекций (конкурирующие точки )

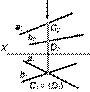
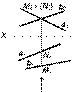
Для определения видимости прямых относительно плоскостей проекции используются конкурирующие точки. Рассмотрим комплексный чертеж скрещивающихся прямых а и b (рис. 4.1 и рис. 4.2). Определим, какая из прямых расположена выше другой (относительно плоскости p₁) или ближе другой к наблюдателю (относительно плоскости p₂). Для этого необходимо проанализировать положение конкурирующих точек С и D, принадлежащих этим прямым. Из рис. 4.1 следует, что при взгляде сверху по указанной стрелке С₂ выше D₂ относительно p₁. Следовательно, точка С₁, принадлежащая прямой а, будет видима, а точка D₂, принадлежащая прямой b, (D₁ – показана в скобках) будет не видима. Из двух конкурирующих точек M и N, принадлежащих скрещивающимся прямым а и b (рис. 4.2), относительно плоскости p₂, видимой будет точка М₂, так как М₁ расположена ближе к наблюдателю, что видно при взгляде спереди по указанной стрелке, а точка N₂ будет не видима, поэтому она показана в скобках.

Рис. 4.1	Рис. 4.2

Date: 2015-04-23; view: 458; Нарушение авторских прав