Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Определение удлинений и сдвигов для произвольно направленных волокон
|
|
Рассмотрим частицу тела, отнесённую к координатным осям x, y, z (рис. 3.29).
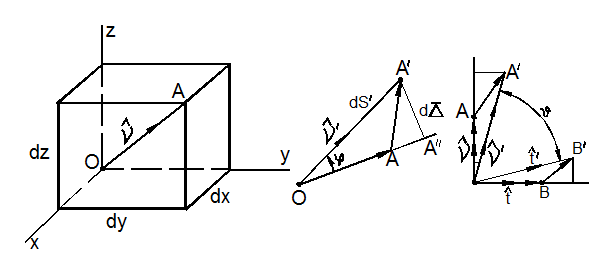
а) б) в)
Рис. 3.29
Направление диагонали ОА = dS определим до деформации единичным вектором:
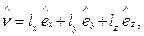(69)
а после деформации – единичным вектором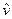 
, повёрнутым на угол 
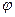. После деформации длина волокна изменится и станет равной ОА’ = dS’, так, что будет выполнено векторное равенство:
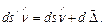(70)
Волокно ОА получит относительную деформацию:
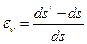, (71)
откуда
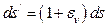. (72)
Соотношение (70), с учётом (71), (72), запишем в виде:
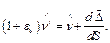(73)
Соотношение (73) названо профессором Л.А. Толоконниковым (1923 – 1998) фундаментальным соотношением теории деформаций.
Так как вектор перемещения
,
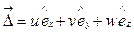то
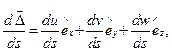(74)
где
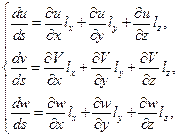(75)
Возводя (73) в квадрат, получим:
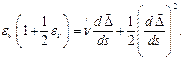(76)
Считая деформации малыми по сравнению с единицей и пренебрегая в (76) нелинейными членами, находим:
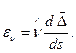(77)
Учитывая (69), (74), (75) и производя скалярное умножение, находим:
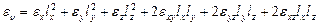(78)
где обозначено:
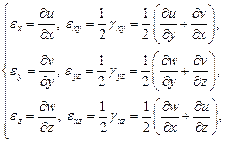(79)
Формулы (79) связывают компоненты малой линейной деформации и перемещения и носят название геометрических соотношений Коши для деформаций.
Рассмотрим теперь два ортогональных волокна, направление которых характеризуется единичными векторами:
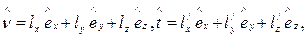
где
.
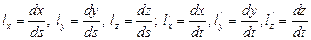Для них можно составить два фундаментальных соотношения (рис. 3.29, в):
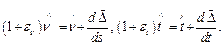(80)
Для производной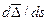 
имеем соотношение (74), а для 
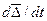аналогичное соотношение с заменой ds на dt.
В результате перемножения соотношений (80) получим:
.
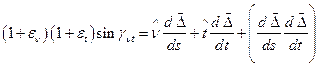Считая деформации малыми и пренебрегая нелинейными слагаемыми, находим:
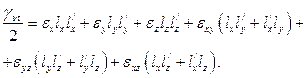(81)
Легко установить геометрический смысл введённых в формулах Коши (79) обозначений, названных компонентами малой линейной деформации.
Пусть мы имеем волокно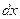 
. Для него 
, 
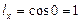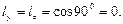
Из (79) получаем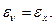 
Следовательно, 
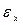есть действительно относительное удлинение частицы вдоль оси 
. Аналогично выясняется геометрический смысл компонент деформации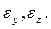 
Пусть теперь мы имеем два ортогональных волокна 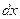и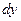 
. Тогда для первого 
а для второго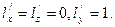 
Из (81) получаем 
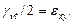Следовательно, 
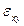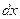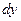представляет собой половины сдвига между волокнами и . Аналогично можно выяснить геометрический смысл остальных компонент: 
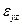и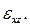 
В частном случае плоской деформации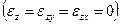 
имеем:
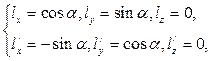
и из формул (78), (81) следуют полученные нами ранее формулы
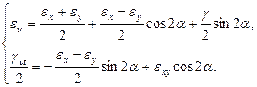(82)
Формулы Коши (35) можно получить значительно проще. Рассмотрим одну из граней ОАСВ частицы тела в плоскости ху со сторонам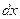и и 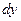(рис. 3.30). В результате малой линейной деформации эта грань элемента удлинится в направлениях осей х, у и изменит прямой угол на величину деформации сдвига 
.
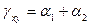Рассмотрим деформацию волокна ОА = dx. Её можно вычислить следующим образом. Представим сначала, что волокно переместилось в положение О/А/ = dx как жёсткое целое, сохранив свою длину. Затем волокно удлинилось на величину А//А/// и по перпендикуляру А///А/ перешло в положение ОА/.
В соответствии с принципом малости перемещений перемещение А///А/ не вызывает дополнительного удлинения волокна ОА.
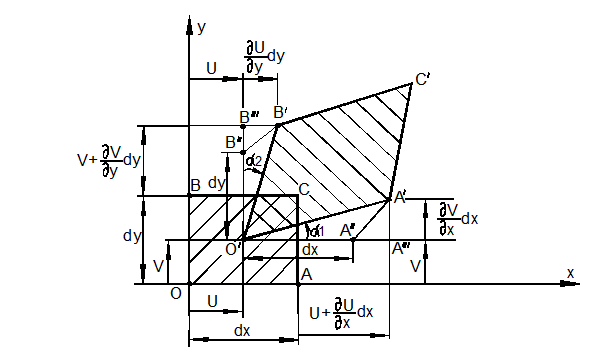
Рис. 3.30
Поэтому
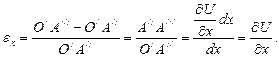
Аналогично можно найти деформации в направлениях осей y и z:
Рассмотрим теперь деформацию сдвига между волокнами ОА и ОВ (рис. 3.30). Малые углы поворота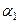 
и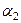 
волокон отождествим с их тангенсом. Тогда:
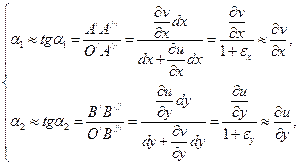
где считается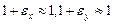 
в силу малости относительных деформаций по сравнению с единицей.
Таким образом:
Аналогично находим деформации сдвига (угловые деформации) в двух других координатных плоскостях.
В результате получаем шесть геометрических зависимостей Коши между компонентами тензора деформации и составляющих перемещения:
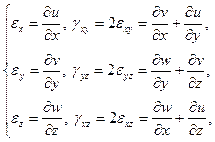(83)
Деформации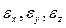 
считаются положительными, если отвечают удлинениям волокон, и отрицательными, если они укорачиваются. Положительные сдвиги отвечают уменьшению прямого угла между положительными направлениями координатных осей. Отрицательные сдвиги отвечают увеличению прямого угла между этими же волокнами.
Объёмная деформация
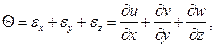
т.е. может быть выражена через составляющие перемещения.
Date: 2015-05-22; view: 682; Нарушение авторских прав