
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Принятие решения
|
|
При принятии решения о повышении качества выпускаемой системы – стиральная машина, фирме-производителю необходимо учитывать следующие внешние системы:
- потребителей, которые предъявляют определённые требования к качеству продукции;
- маркетинговую систему, так как сначала необходимо выяснить, какие именно требования предъявляют потребители;
- систему своих собственных внутрифирменных ресурсов (человеческих, материальных, финансовых);
- производственную систему, то есть производственные возможности и производственные мощности;
- систему поставщиков, от которых зависит качество сырья и комплектующих;
- технологическую систему, от которой зависит возможность улучшения качественных показателей и технология изготовления;
- экономическую систему, от которой зависят финансовые условия деятельности фирмы и выбор стратегии (конкуренция, прибыль, ценообразование, налоги);
- систему обеспечения и обслуживания, от которой зависит уровень обслуживания и наличие запасных частей в ремонтных мастерских.
Задача № 26. Процесс сборки изделия (автомобиля, прибора и т.п.) можно рас-сматривать как систему, элементами которой являются отдельные операции. Их взаимосвязь представлена матрицей инциденций, приведенной в таблице. По данным таблицы постройте уровни порядка следования операций по очередности. Итоговый результат представьте в виде порядкового графа.
Таб.2 Исходные данные
| Операции | O 1 | O 3 | O 4 | O 5 | O 7 | O 8 | O 9 | O 10 | O 11 | O 12 | O 13 |
| O 1 | |||||||||||
| O 3 | |||||||||||
| O 4 | |||||||||||
| O 5 | |||||||||||
| O 7 | |||||||||||
| O 8 | |||||||||||
| O 9 | |||||||||||
| O 10 | |||||||||||
| O 11 | |||||||||||
| O 12 | |||||||||||
| O 13 |
Решение
Определим систему в виде S = {х; R}, где х – множество автомобилей, R - отношение порядка.
Шаг1.
Составим векторную строку А0, равную сумме строк исходной матрицы
А0 = {25102011111}
Нули в строке А0 дают операции, которые предшествуют другим.
В нашем случае это операции (О5, О8) – они образуют первый порядковый уровень N0 – первый порядковый уровень.
Шаг 2.
Преобразуем строку А0 следующим образом: нули заменим знаком х, исключим из строки значения, соответствующие нулевым операциям, для чего зачеркнем одинаковым способом строки О5 и О8
В итоге получим строку А1 = {240х1х00111}
Новые нули в строке А1 дают элементы: О4,О9,О10, они образуют порядковый уровень N1.
Шаг3.
Преобразуем строку А1, исключая значения, соответствующие нулевым элементам, и заменяя предыдущие нули крестом.
В итоге получим строку А2={03хх0ххх101}. Появившиеся новые нули соответствуют элементам О1, О7,О12 образующему N2 порядковый уровень.
Шаг 4.
Преобразуем строку А2, исключая значения, соответствующие нулевым элементам, и заменяя предыдущие нули крестом, в итоге получим строку А3= {х2хххххх0х0}. Появившиеся нули соответствуют О11 и О13 элементам, образующую N3 порядковый уровень.
Шаг 5.
Преобразуем строку А3, исключая значения, соответствующие нулевым элементам, получим строку А4= {х0ххххххххх}, появившиеся нули соответствую – O3 элементу, образуя- N4 порядковый уровень.
Результаты показывают, что элементы множества располагаются по уровням порядка следующим образом: N0- {O5, О8}, N1 – { О4,О9,О10}, N2 – { О1, О7,О12 }, N3 – { О11,О13}, N4 – {О3}

Задача № 28. По результатам испытаний приборостроительной продукции бы-ли выявлены типовые причины неисправностей и проведено их ранжирование по ряду признаков. Соответствующая матрица инциденций дана в таблице. Постройте уровни порядка на множестве неисправностей по отношению предпочтения («не менее важен, чем»). Итоговый результат представьте в виде порядкового графа. Дайте возможную интерпретацию полученных результатов.
Таб. 3 Исходные данные
| Неисправности | x 1 | x 3 | x 4 | x 5 | x 7 | x 8 | x 9 | x 10 | x 11 |
| x 1 | |||||||||
| x 3 | |||||||||
| x 4 | |||||||||
| x 5 | |||||||||
| x 7 | |||||||||
| x 8 | |||||||||
| x 9 | |||||||||
| x 10 | |||||||||
| x 11 |
Решение:
Построим диагностическую систему S={x, R}, где элементы множества x – являются неисправности x={X1, X2…….X10} множество причин неисправностей.
Зададим отношение R – отношение предподчтения.
Причина хi не менее важна, чем хj.
В этой строке А0 не содержит нулей, т.е. в матрице имеются циклы. Нужно объединить элементы, связанные циклом в группы эквивалентности.
Строка1
Исходный элемент х1 связан сам с собой и с х7. Смотрим строку х7. Наша цель – установить, если ли обратный путь из х7 в х1. Элемент х7 связан сам собой и с х11. Смотрим элемент х11, который связан сам собой, с х7, х6, х1 (получаем цикл).
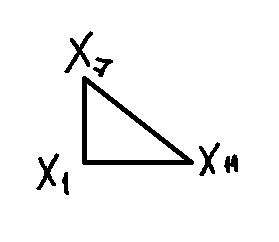
С1
Строка 2
Исходный элемент х3, связан сам с собой с х4, х9 и х10. Элемент х4 связан сам с собой и х5 путь к х3 не ведет, х9 связан сам с собой и с х3(возврат в х3). Элемент х10 связан сам с собой и с х4, х5, х9 и х1 путь к х3 ведет через х9 (цикл).
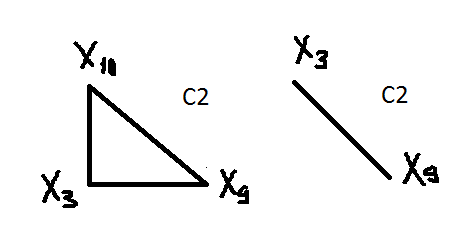
Строка 3
Исходный элемент х4 связан сам с собой и с х5, элемент х5 связан сам с собой и с х4 (возврат к х4)
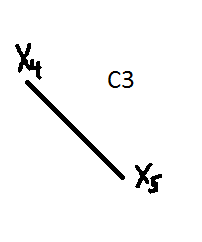
Элемент х5 не рассматривается, так как вошел в С3.
Элемент х7 вошел в С1.
Исходный элемент х8 – автоцикл. (С4)
Элемент х9 вошел в С2.
Х10 – вошел в С2.
Х11 – вошел в С1.
Наша матрица содержит 4 класса эквивалентности.
Преобразуем исходную матрицу, используя информацию о циклах. Заменим в матрице единицы на нули для всех элементов, попавших в один и тот же класс эквивалентности.
| Неисправности | x 1 | x 3 | x 4 | x 5 | x 7 | x 8 | x 9 | x 10 | x 11 |
| x 1 | |||||||||
| x 3 | |||||||||
| x 4 | |||||||||
| x 5 | |||||||||
| x 7 | |||||||||
| x 8 | |||||||||
| x 9 | |||||||||
| x 10 | |||||||||
| x 11 |
Преобразованная матрица циклов не содержит, применим к ней метод, рассмотренный в предыдущей задаче, образуем строку А0.
А0={202210111}
Выпишем нулевые элементы: х3х7х8 – N0
Шаг 2
Преобразуем строку А0. Получим А1={2х121х100}
Выпишем нулевые элементы: х10, х11 –N1
Шаг 3
Преобразуем строку А1, получим строку А2 = {0х001х0хх }
Выпишем нулевые элементы: х1х4х5х9 – N2
Шаг 4.
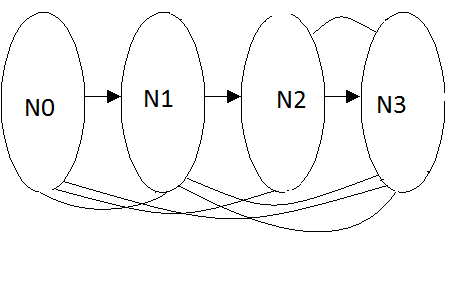
Преобразуем строку А2 – получим А3 = {х х х х 0 х х х х}
Выпишем элемент х7 – N3
Задача № 76. По данным приведенной ниже таблицы определите наилучший вариант решения, используя следующие методы: аддитивная свертка, мультипликативная свертка, свертка по наихудшему критерию, свертка по наилучшему критерию, метод главного критерия. Задачу решите для двух случаев: а) важность критериев одинакова; б) важность критериев составляет соответственно a1 = 0,26, a2 = 0,21, a3 = 0,15, a4 = 0,18.
| Варианты | K 1 | K 2 | K 3 | K 4 | K 5 |
| B 1 | |||||
| B 2 | |||||
| B 3 | |||||
| B 4 | |||||
| B 5 | |||||
| B 6 | |||||
| B 7 |
Решение:
По первому варианту:
Date: 2015-05-22; view: 815; Нарушение авторских прав