Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
используя свойства
КОНТРОЛЬНАЯ РАБОТА № 1
ЛИНЕЙНАЯ АЛГЕБРА
I. Решить систему линейных уравнений
1) по формулам Крамера;
2) методом Гаусса;
3) методом обратной матрицы (выполнить проверку).
| 1. | x1-x2+2x3 =2 3x1+x2-x3 =3 4x1-x2-5x3 =-2 | 16. | 6x1+6x2+2x3=-11 11x1+9x2+2x3=-22 4x1+5x2+2x3=-5 | |
| 2. | x1+8x2-5x3=-7 3x1+2x2+x3=1 2x1-3x2+2x3=9 | 17. | 12x1+6x2+x3=5 19x1+16x2+7x3=256 x1+ x2 =-2 | |
| 3. | 3x1-3x2-4x3=-1 6x1-6x2+x3=0 4x1-9x2-2x3=-3 | 18. | 4x1+3x2+2x3=1 4x1+5x2+2x3=3 3x1+2x2+3x3=5 | |
| 4. | 3x1+4x2+7x3=1 -2x1+5x2-3x3=1 5x1-6x2+11x3=-3 | 19. | 6x1+9x2+4x3=-8 -x1-x2+x3=2 10x1+16x2+7x3=-15 | |
| 5. | 2x1-x2-x3=4 3x1+4x2-2x3=11 3x1-2x2+4x3=11 | 20. | x1+x2+x3=-1 3x1+4x2+3x3=-6 9x1+8x2+5x3=-10 | |
| 6. | 2x1+x2-x3=-1 2x1-x2+2x3=-4 4x1+x2+4x3=-2 | 21. | -x1+3x2-2x3=2 2x1-x2+3x3=1 2x1-3x2+4x3=-1 | |
| 7. | x1+2x2-2x3=-3 2x1+x2-2x3=0 3x1+x2+4x3=6 | 22. | 3x1+2x2+2x3=-1 2x1+5x2+3x3=-6 3x1+4x2+4x3=-5 | |
| 8. | x1+2x2+3x3=5 x1+3x2+2x3=1 3x1+x2+2x3=11 | 23. | 2x1+4x2+3x3=0 x1+5x2+4x3=-3 -3x1+5x2+3x3=-11 | |
| 9. | 4x1+x2+2x3=-2 -x1+2x2+3x3=5 -2x1+3x2+x3=8 | 24. | 2x1+2x2+x3=2 3x1+3x2+x3=1 2x1-x2 =8 | |
| 10. | 4x1+2x2+x3=31 2x1+x2+5x3=29 x1-x2+3x3=10 | 25. | x1+3x2+5x3=-8 x1+4x2+8x3=-15 x1+2x2+6x3=-13 | |
| 11. | 6x1+7x2+3x3=2 3x1+x2-2x3=2 2x1+2x2+x3=1 | 26. | 2x1-4x2+9x3=28 7x1+3x2-6x3=-1 7x1+9x2-9x3=5 | |
| 12. | 9x1+9x2+5x3=2 4x1-x2-2x3=-5 14x1+13x2+7x3=-1 | 27. | x1+x2-x3=36 x1-x2+x3=13 x1-x2-x3=-7 | |
| 13. | -2x1+3x2+4x3=5 3x1-x2-3x3=-1 -x1+2x2+2x3=3 | 28. | x1+2x2+x3=4 3x1-5x2+3x3=1 2x1+7x2-x3=8 | |
| 14. | 3x1+3x2+x3=8 7x1+6x2+2x3=18 7x1+9x2+2x3=21 | 29. | 7x1+2x2+3x3=15 5x1-3x2+2x3=15 10x1-11x2+5x3=36 | |
| 15. | 9x1+7x2+3x3=-10 14x1+9x2+4x3=-15 3x2+2x3=5 | 30. | x1+x2+x3=36 2x1 -3x3=-17 6x1 -5x3=7 |
II. Вычислить определитель данной матрицы двумя способами:
По определению;
используя свойства.
| 1. |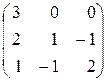 
| 16. |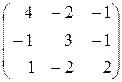 
| |
| 2. |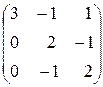 
| 17. |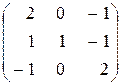 
| |
| 3. |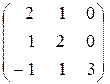 
| 18. |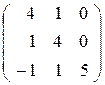 
| |
| 4. |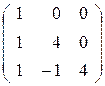 
| 19. |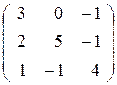 
| |
| 5. |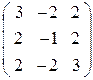 
| 20. |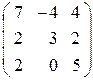 
| |
| 6. |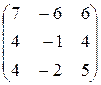 
| 21. |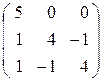 
| |
| 7. |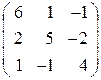 
| 22. |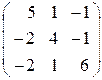 
| |
| 8. |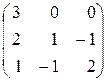
| 23. |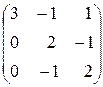
| |
| 9. |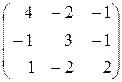
| 24. |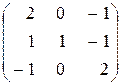
| |
| 10. |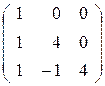
| 25. |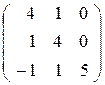
| |
| 11. |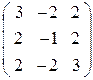
| 26. |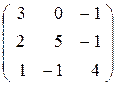 
| |
| 12. |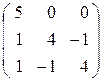
| 27. |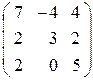
| |
| 13. |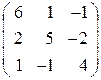
| 28. |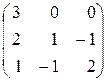
| |
| 14. |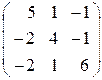
| 29. |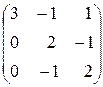
| |
| 15. |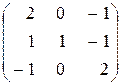
| 30. |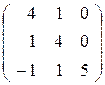 
|
III. Даны точки A, B, C, D. Положим а =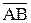 
, b = 
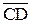. Найти:
1) векторы c =2 а + b и d = а -2 b;
2) модули векторов | c| и | d|;
3) скалярное произведение (c × d);
4) векторное произведение [ c;d ];
5) угол между векторами c и d.
| 1. | A(1,0,2) | B(-1,2,3) | C(2,3,1) | D(-3,4,5,) |
| 2. | A(0,3,-2) | B(4,1,3) | C(-1,1-1,) | D(3,2,4) |
| 3. | A(-1,-1,0) | B(1,1,1) | C(-2,1,0) | D(0,-2,7) |
| 4. | A(0,2,0) | B(-2,0,0) | C(3,1,0) | D(0,-1,-3) |
| 5. | A(2,1,-1) | B(-1,-3,-1) | C(0,-1-1,) | D(2,4,1) |
| 6. | A(2,2,-1) | B(0,0,0) | C(0,-4,0) | D(2,0,0) |
| 7. | A(-3,2,4) | B(-3,-3,4) | C(0,-3,4) | D(-1,-1,4) |
| 8. | A(5,6,1) | B(6,1,4) | C(1,2,3) | D(2,0,2) |
| 9. | A(-5,6,0) | B(-6,-2,1) | C(-3,4,-1) | D(-1,-7,0) |
| 10. | A(10,9,0) | B(9,8,1) | C(8,7,1) | D(7,6,0) |
| 11. | A(7,7,0) | B(5,6,0) | C(4,5,1) | D(3,4,1) |
| 12. | A(-5,-2,0) | B(-3,-3,1) | C(0,5,0) | D(9,6,1) |
| 13. | A(-1,0,-1) | B(1,1,-1) | C(1,2,-3) | D(0,-2,-4) |
| 14. | A(1,6,2) | B(-1,0,1) | C(4,2,3) | D(-1,-1,4) |
| 15. | A(3,6,4) | B(3,5,3) | C(2,4,2) | D(1,0,1) |
| 16. | A(7,2,7) | B(9,1,7) | C(9,7,6) | D(-1,-1,7) |
| 17. | A(4,-3,2) | B(1,-7,2) | C(-1,0,1) | D(1,1,1) |
| 18. | A(0,-5,3) | B(2,2,2) | C(0,-3,1) | D(7,7,2) |
| 19. | A(1,6,7) | B(0,6,7) | C(-4,5,6) | D(-4,-4,8) |
| 20. | A(2,1,-1) | B(-1,-3,-1) | C(0,-1-1,) | D(2,4,1) |
| 21. | A(1,3,2) | B(4,-1,3) | C(8,1-1,) | D(3,2,0) |
| 22. | A(0,2,-4) | B(-2,1,0) | C(-3,1,7) | D(0,-1,3) |
| 23. | A(2,-5,-1) | B(0,3,-9) | C(3,-4,7) | D(2,0,5) |
| 24. | A(5,-6,1) | B(4,1,-4) | C(1,-4,3) | D(-2,0,3) |
| 25. | A(1,9,0) | B(-5,8,1) | C(-3,7,1) | D(0,6,5) |
| 26. | A(5,-2,0) | B(-3-3,1) | C(7,5,4) | D(-3,6,1) |
| 27. | A(1,-6,0) | B(1,0,-1) | C(7,2,-3) | D(-1,1,4) |
| 28. | A(5,2,-7) | B(4,1,7) | C(5,=3,6) | D(1,-5,7) |
| 29. | A(-1,-5,3) | B(2,-6,0) | C(0,3,1) | D(3,7,2) |
| 30. | A(5,-6,0) | B(6,-2,1) | C(-3,4,0) | D(-1,-7,3) |
IV. Даны вершины треугольника A, B, C. Найти:
1) длину стороны AB;
2) уравнение стороны AC;
3) уравнение высоты, проведенной через вершину B;
4) уравнение медианы, проведенной из вершины C;
5) площадь треугольника АВС.
| 1. | A(1,0) | B(-1,2) | C(2,3) |
| 2. | A(0,3) | B(4,1) | C(-1,1) |
| 3. | A(-1,-1) | B(4,1) | C(-2,1) |
| 4. | A(0,2) | B(-2,0) | C(3,1) |
| 5. | A(2,1) | B(-1,-3) | C(0,-1) |
| 6. | A(2,2) | B(0,0) | C(0,-4) |
| 7. | A(-3,2) | B(-3,-3) | C(0,-3) |
| 8. | A(5,6) | B(6,1) | C(1,2) |
| 9. | A(-5,6) | B(-6,-2) | C(-3,4) |
| 10. | A(10,9) | B(9,8) | C(8,7) |
| 11. | A(6,7) | B(5,6) | C(4,5) |
| 12. | A(10,9) | B(9,8) | C(8,7) |
| 13. | A(-5,-2) | B(-3,-3) | C(0,5) |
| 14. | A(-1,0) | B(1,1) | C(1,2) |
| 15. | A(1,6) | B(-1,0) | C(4,2) |
| 16. | A(3,6) | B(3,5) | C(2,4) |
| 17. | A(7,2) | B(9,1) | C(9,7) |
| 18. | A(0,-3) | B(-1,-2) | C(3,3) |
| 19. | A(4,-3) | B(1,-7) | C(-1,0) |
| 20. | A(0,-5) | B(2,2) | C(0,-3) |
| 21. | A(1,-6) | B(0,3) | C(-4,9) |
| 22. | A(0,-3) | B(2,1) | C(-1,5) |
| 23. | A(-4,3) | B(2,6) | C(-5,1) |
| 24. | A(2,4) | B(0,-2) | C(1,-4) |
| 25. | A(5,-3) | B(0,1) | C(-1,2) |
| 26. | A(1,9) | B(-2,8) | C(8,0) |
| 27. | A(-1,6) | B(9,1) | C(1,-2) |
| 28. | A(3,-6) | B(3,8) | C(-3,4) |
| 29. | A(5,-3) | B(-1,2) | C(1,-3) |
| 30. | A(0,5) | B(2,-7) | C(6,4) |
V. Даны четыре точки A, B, C и D (координаты точек взять из задания III).
1) Составить уравнение плоскости, проходящей:
* через точку A и имеющей нормальный вектор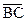 
;
* через точки A, B, C.
2) Вычислить расстояние от точки D до плоскости, проходящей через точки A, B, C.
3) Составить канонические и параметрические уравнения прямых, проходящих через точки A и C, а также B и D. Будут ли эти прямые перпендикулярны? Параллельны?
Date: 2015-04-23; view: 381; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |