Эрмитовы операторы

Операторы, соответствующие физическим величинам в квантовой механике, обладают следующим свойством:

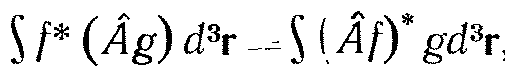
(2.17)

где f (r) и g (r) — две произвольные функции.

Оператор, обладающий свойством (2.17), называется эрмитовым.
Легко показать, что, например, оператор — i¶/¶x является, т. е. для любых функций f и g, таких, что fg→ 0 при х →∞, выполняется соотношение

(2.18)

Эрмитово сопряженные операторы. Для любого данного линейного оператора А всегда существует другой оператор В, называемый эрмитово сопряженным оператором оператору :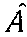

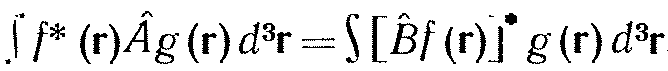
(2.19)

где f и g — две произвольные функции. Для эрмитово сопряженного оператора используется обозначение

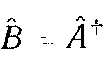
которое словами читается «А с крестом».

Таким образом, формулу (2.19) можно записать в виде

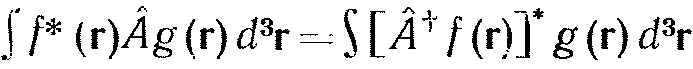
(2.20)

Сравнивая (2.20) с (2.17), видим, что оператор 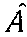эрмитов в том случае, когда эрмитово сопряженный ему оператор совпадает с ним самим. Иными словами, любой эрмитов оператор 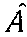удовлетворяет условию

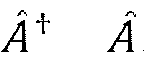
(2.21)

9) мат. аппарат кв. механики:функционалы в линейном векторном пространстве Гильберта.
Функционалом называют правило,ставящие числа в соответствии некоторой функции.
Пространство линейных непрерывных (ограниченных) функционалов также образует линейное пространство и называется сопряжённым пространством.

Имеет место следующая теорема Риса об общем виде ограниченного линейного функционала в гильбертовом пространстве: для любого линейного ограниченного функционала 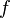на гильбертовом пространстве 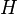существует единственный вектор такой, что 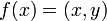для любого 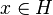. При этом норма линейного функционала 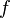совпадает с нормой вектора :

• .

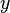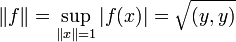Из теоремы следует, что пространство линейных ограниченных функционалов над гильбертовым пространством 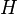подобно самому пространству .

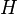10) мат. аппарат кв. механики: представление Дирака для векторов, ортонормированных базисов векторов пространства Гильберта, матричного представления линейных и эрмитовых операторов

Все ортонормированные базисы в гильбертовом пространстве имеют одинаковую мощность, что позволяет определить размерность гильбертова пространства как размерность произвольного ортонормированного базиса (ортогональная размерность). Гильбертово пространство сепарабельно тогда и только тогда, когда имеет счётную размерность.

Размерность пространства также можно определить как наименьшую из мощностей подмножеств гильбертова пространства 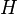, для которых замыкание линейной оболочки совпадает с .

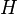Любые два гильбертовы пространства, имеющие одинаковую размерность, изоморфны. В частности, любые два бесконечномерные сепарабельныегильбертовы пространства изоморфны друг другу и пространству.

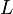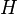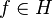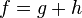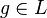Пусть -некоторое подпространство в гильбертовом пространстве . Тогда для любого элемента справедливо единственное разложение , где , а 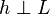. Элемент 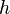называется проекцией элемент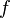а на 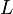. Совокупность элементов 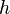, ортогональных подпространству 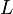образует (замкнутое) подпространство 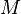, являющееся ортогональным дополнением подпространства .

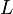Говорят, что пространство 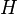разложено в прямую сумму подпространств 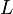и 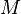, что записывается как 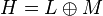. Аналогично можно записать .

Date: 2015-05-19; view: 1012; Нарушение авторских прав