Движение по кривой

Рис. 2.7.1.

Рассмотрим движение материальной точки по произвольной кривой. Для простоты, будем считать эту кривую плоской, все точки такой кривой лежат в одной плоскости.

Предположим, что в момент времени t материальная точка оказалась в точке M кривой (рис. 2.7.1). Возьмем два положения материальной точки - в момент времени t -D t (точка M₁) и момент времени t +D t (точка M₂). Через три точки M₁, M и M₂ можно провести единственную окружность. На рис. 2.7.1 это окружность C₁. Уменьшим приращение времени D t и через новые точки проведем окружность C₂. Дальнейшее уменьшение D t приведет к последовательности окружностей 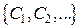. В курсе математического анализа доказывается, что у этой последовательности существует предел (окружность C на рис. 2.7.1).

Соприкасающейся окружностью в точке M плоской кривой называется предел последовательности окружностей, проходящих через три точки рассматриваемой кривой, одна из которых точка M, при неограниченном приближении двух других точек к точке M.

Центр соприкасающейся окружности и ее радиус называются соответственно центром кривизны и радиусом кривизны рассматриваемой кривой в точке M.

Пользуясь результатами предыдущего параграфа, можно найти ускорение в некоторой точке M криволинейной траектории.

a = a _n + a _t., (2.7.1)

где 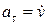- тангенциальное ускорение, 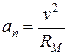- нормальное ускорение, R_M – радиус кривизны траектории в точке M.

Физический метод определения радиуса кривизны.

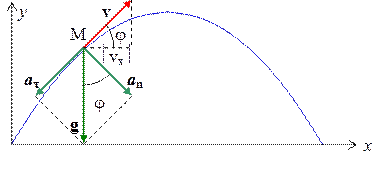
Рис. 2.7.2.

Найдем, для примера, радиус кривизны параболы в некоторой точке M. Парабола – это траектория движения тела, брошенного под углом к горизонту (см. рис. 2.7.2). Ускорение тела a = g можно представить как сумму нормального и тангенциального ускорений: g = a _n + a _t. Т.к. 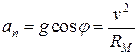, то радиус кривизны R _M параболы в некоторой точке M вычисляется по формуле: 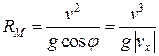= 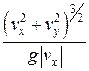. Проекции скорости v _x (t) и v _y (t) рассчитываются по формулам из §5.

Date: 2015-05-19; view: 659; Нарушение авторских прав