скорость перемещения жидкой частицы в общем случае слагается из скоростей трех движений: поступательного, вращательного и деформационного

ДВИЖЕНИЕ ЖИДКОЙ ЧАСТИЦЫ

Поступательное, вращательное и деформационное движение. Теорема Коши – Гельмгольца. Скорость линейной и угловой деформаций. Вихрь скорости.

При течении жидкости ее элементарные объемы совершают сложное движение. Они могут двигаться поступательно, вращаться и деформироваться. Последнее связано с тем, что частицы жидкости весьма подвижны и легко смещаются относительно друг друга.

«В общем случае движение жидкой частицы является сложным. Наряду с поступательным движением вдоль некоторой траектории частица может вращаться относительно собственных осей и в процессе этого движения деформироваться».

& (Дейч) с. 9

Скорость движения жидкой частицы определяется по теореме Коши — Гельмгольца, которая формулируется так:

скорость перемещения жидкой частицы в общем случае слагается из скоростей трех движений: поступательного, вращательного и деформационного.

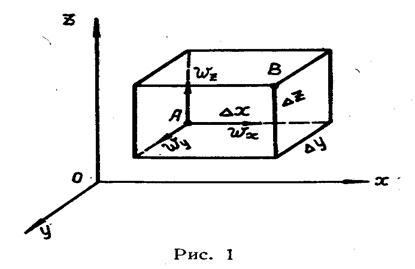
Для вывода формулы Коши — Гельмгольца рассмотрим элементарный объем жидкости, взятый в форме прямоугольного параллелепипеда – рисунок 1. В точке А, имеющей координаты х, у, z, составляющие скорости жидкости равны

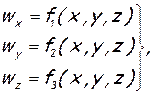(1.1)

где ƒ₁, ƒ₂, и ƒ₃ — функции, определяющие величины проекций скорости в зависимости от координат. При переходе к точке В эти величины изменятся и будут равны

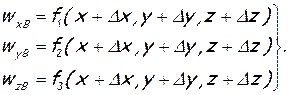(1.2)

Правые части уравнений (1.2) разложим в ряд Тейлора по формуле для функции многих переменных. При этом отбросим бесконечно малые второго и более высоких порядков, а также примем во внимание зависимости (1.1).

Тогда

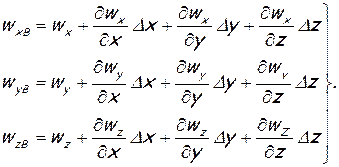(1.3)

Чтобы выделить в явном виде скорости трех, указанных выше в формулировке теоремы Коши — Гельмгольца видов движения (поступательного, вращательного и деформационного), прибавим и вычтем в правой части каждого из уравнений (1.3) следующие члены соответственно:

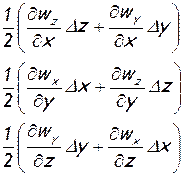
После перегруппировки членов первое уравнение системы (1.3) примет вид

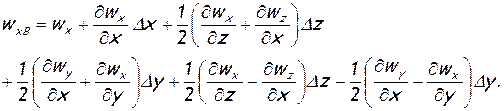(1.4)

Аналогичные выражения для двух других проекций скорости w_y и w_z рекомендуем записать самостоятельно. А сейчас рассмотрим, в чем заключается смысл членов, входящих в правую часть выражения (1.4).

Нетрудно заметить, что 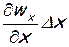представляет собой скорость линейной деформации растяжения. Иначе говоря, это есть удлинение элемента жидкости в единицу времени в направлении оси x.

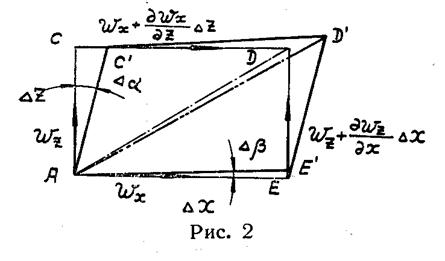
Для того чтобы уяснить смысл третьего и четвертого слагаемого правой части формулы (1.4), обратимся к рисунку 2, где изображена проекция элементарного объема жидкости на плоскость xoz. В начальный момент времени он (объем) занимает положение ACDE. Так как составляющая скорости w_x в точке С больше, чем в точке А, а w_z в точке Е больше, чем в точке А, то грани параллелепипеда перекашиваются, и он за время dt занимает положение AC'D'E'. Углы поворота граней АС и АЕ равны

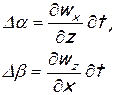
(здесь, вследствие малости углов, сами углы и их тангенсы приняты одинаковыми). Угловую деформацию элемента жидкости характеризуют средней арифметической величиной углов поворота его сторон

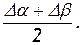
Взяв от этой величины производную по времени, получим скорость угловой деформации в плоскости xoz, т.е. относительно оси у

 

 

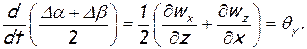
Рассматривая аналогичную картину в других плоскостях, можно получить скорости угловой деформации относительно осей х и z. Окончательно имеем:

 

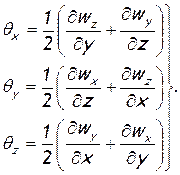(1.5)

 

 

Рассматривая рисунок 2, можно также заключить, что полуразность углов 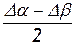равна углу, на который поворачивается диагональ AD. Производная от этой величины по времени дает угловую скорость элементарного объема относительно соответствующей оси. Следовательно,

 

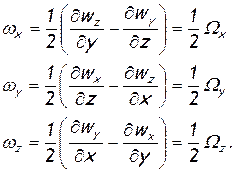(1.6).

 

Вектор 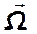называется вихрем скорости [1]. Он совпадает по направлению с вектором угловой скорости и численно равен его удвоенной величине.

Сделав соответствующие подстановки из формул (1.5) и (1.6) в равенство (1.4) и повторив весь вывод для проекций скорости w_x и w_y, получим следующие формулы скорости перемещения жидкого элементарного объема:

 

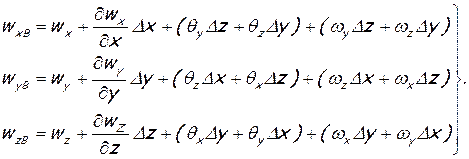(1.7)

 

Эти же формулы пригодны для определения и скорости перемещения жидкой частицы, так как если объем жидкости устремить к нулю, то он будет охватывать лишь одну жидкую частицу. Следовательно, в формулах (1.7) нужно только заменить Δ x, Δ y и Δ z на dх, dу и dz.

Таким образом, рассматривая правую часть формулы (1.7), видим, что она слагается из скорости в исходной точке и приращения скорости, которое включает в себя скорости линейной и угловой деформаций (второе и третье слагаемое) и скорость вращательного движения (четвертое слагаемое), что соответствует формулировке теоремы Коши — Гельмгольца: скорость перемещения жидкой частицы в общем случае слагается из скоростей трех движений - поступательного, деформационного и вращательного.

[1] Заметим, что в теории поля вихрь скорости записывается в виде такого оператора, называемого ротором вектора скорости.

 

Date: 2015-05-19; view: 783; Нарушение авторских прав