Из выражения (20.2) видно, что

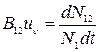(20.4)

– это вероятность перехода за единицу времени, сопровождающегося поглощением, в расчете на одну частицу. Таким образом, коэффициент Эйнштейна имеет вероятностный (статистический) смысл.

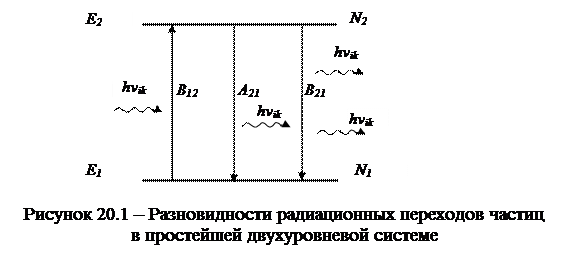Процесс испускания электромагнитного излучения может происходить в соответствии с двумя механизмами: спонтанно (вследствие внутренних причин) и вынужденно (при воздействии возбуждающего излучения).

Общее число частиц, совершающих за время dt спонтанные переходы 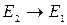, прямо пропорциональна населенности уровня, соответствующего исходному состоянию системы:

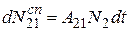. (20.5)

Энергию электромагнитного излучения, спонтанно испущенного атомами (молекулами), находящимися в единичном объеме вещества, за время 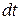, можно представить в виде:

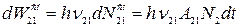. (20.6)

Из формулы (20.5) выразим величину :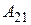

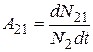(20.7)

– коэффициент Эйнштейна, имеющий смысл вероятности перехода, сопровождающегося спонтанным испусканием электромагнитного излучения одной частицей за единицу времени.

Вынужденное испускание происходит под действием внешнего (вынуждающего) излучения. Число вынужденных излучательных переходов за время dt в рассматриваемой системе уровней прямо пропорционально населенности N₂ уровня, соответствующего исходному состоянию системы (E₂) и объемной спектральной плотности энергии внешнего (возбуждающего) излучения u₁₂:

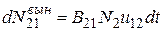. (20.8)

Энергия вынужденного излучения, испущенного в единичном объеме вещества за время dt, запишем в виде:

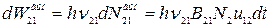. (20.9)

Из формулы (20.8) легко выделить величину

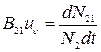(20.10)

– вероятность перехода, совершаемого одной частицей за единицу времени и сопровождающегося вынужденным испусканием. Здесь 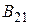– коэффициент Эйнштейна для вынужденных излучательных переходов.

Существенно, что на основе изложенных представлений в 1916 году Эйнштейном строго и изящно была выведена формула Планка для объемной спектральной плотности энергии теплового излучения, частота которого v, при заданной температуре T:

,

а также установлены соотношения между коэффициентами Эйнштейна, для рассматриваемых переходов имеющие вид:

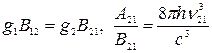, (20.11)

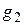где и – статистические веса энергетических уровней и .

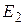Таким образом, внутренними параметрами атомной системы, определяющими энергию электромагнитного излучения, поглощённого или испущенного веществом, и, следовательно, – интенсивность спектральных линий в регистрируемом спектре, являются вероятности переходов в единицу времени, то есть коэффициенты Эйнштейна.

Используя формулы (20.7), (20.10) и (20.11), можно выразить полную вероятность испускания:

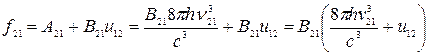. (20.12)

Анализируя формулу (20.12), видим, что при относительно невысоких значениях объемной плотности возбуждающего излучения 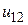вероятность f₂₁ практически полностью определяется вероятностью спонтанных переходов с испусканием энергии. При высокой мощности облучения вероятность вынужденного испускания может стать существенно выше вероятности спонтанного испускания. Такая ситуация имеет место в активной среде генерирующего лазера, а также при использовании лазера в качестве источника возбуждающего излучения.

В состоянии равновесия число переходов, совершаемых с поглощением энергии, равно числу переходов, совершаемых системой атомов (молекул) за это же время с излучением энергии (условие детального равновесия):

.

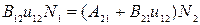Установим, какими физическими параметрами частиц определяются значения коэффициентов Эйнштейна, соответствующие электрическим дипольным переходам. Для этого воспользуемся принципом соответствия, рассматривая свойства атомов и молекул на основе квантового, а свойства электромагнитного излучения – на основе классического описания. Отметим, что такой подход вполне оправдан и сделанные на его основе выводы подтверждены экспериментально.

В классической теории получена следующая формула средней мощности излучения классического осциллятора (величины энергии, испускаемой осциллятором в единицу времени):

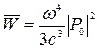, (20.13)

где 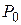– амплитуда электрического дипольного момента осциллятора, 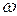– круговая частота испускаемого электромагнитного излучения, 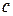– скорость света в вакууме.

Учтём, что в нашем рассмотрении 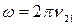, и воспользуемся принципом соответствия результатов квантовой и классической теории, в соответствии с которым 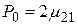( – матричный элемент дипольного момента спонтанного излучательного перехода 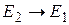), и запишем формулу (20.13) в виде:

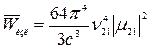. (20.14)

Далее воспользуемся формулой (20.6) и выразим энергию излучения, испускаемого за единицу времени одной частицей спонтанно (что соответствует одному осциллятору в классической модели):

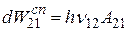. (20.15)

Приравнивая правые части равенств (20.14) и (20.15), выразим коэффициент Эйнштейна 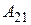, имеющий смысл вероятности спонтанного испускания кванта одной частицей за единицу времени:

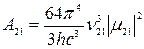. (20.16)

Воспользуемся формулой (20.11) и получим выражения для коэффициентов Эйнштейна 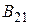и :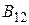

,

.

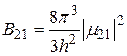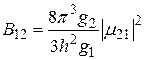Таким образом, коэффициенты Эйнштейна непосредственно связаны с фундаментальными параметрами частиц, какими являются матричные элементы дипольного момента квантовых переходов .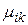

В квантовой механике значение матричного элемента дипольного момента определяется в соответствии с формулой:

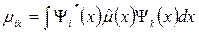, (20.17)

где х – совокупность всех координат соответствующей формы движения; 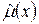– оператор электрического дипольного момента; 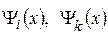– волновые функции, соответствующие исходному и конечному состоянию системы.

Выражение (20.17) используется для определения правил отбора. Функции состояния 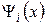и 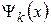зависят от квантовых чисел как от параметров. Правила отбора – это условия для изменения значений квантовых чисел в результате перехода, при которых вероятность излучательного квантового перехода, и, следовательно, матричный элемент перехода, отличны от нуля. Такие переходы называются разрешенными. Переходы, вероятность которых равна нулю, называются запрещенными. Например, правила отбора для переходов в водородоподобной атомной системе имеют вид:

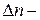любое целочисленное значение ( 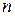– главное квантовое число),

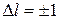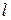( – орбитальное квантовое число),

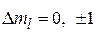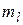( – магнитное квантовое число),

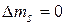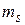( – спиновое квантовое число).

До сих пор мы рассматривали дискретные энергетические уровни, соответствующие строго определенным значениям энергии , поэтому спектральные линии, обусловленные квантовыми переходами, в соответствии с правилом частот Бора, – монохроматические. В реальности каждый энергетический уровень характеризуется некоторой шириной 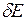, и каждая спектральная линия занимает в спектре некоторый интервал частот 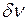. При этом ширина спектральной линии

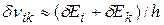. (20.18)

Следовательно, ширина спектральной линии – величина, с использованием которой можно характеризовать степень немонохроматичности излучения, соответствующего данной спектральной линии – .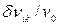

Рассмотрим основные причины уширения спектральных линий частиц вещества, находящегося в газовой фазе, в отсутствие внешних электрических и магнитных полей.

Ширину спектральных линий, соответствующих излучению покоящейся свободной квантовой системы, называют естественной шириной. Теоретическое описание явления естественного уширения спектральных линий проводится в рамках как классической, так и квантовой теории излучения.

Воспользуемся квантовомеханическим соотношением неопределенности для времени и энергии

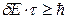, (20.19)

где 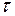– время жизни квантовой системы в рассматриваемом стационарном состоянии.

Из соотношения (20.19) непосредственно вытекает, что бесконечно узким является тот уровень энергии, которому соответствует 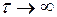, что характерно только для основного энергетического уровня. Естественная ширина возбужденных уровней, характеризующихся малыми значениями времени жизни (~(10^-8 – 10^-4) c), может быть достаточно большой.

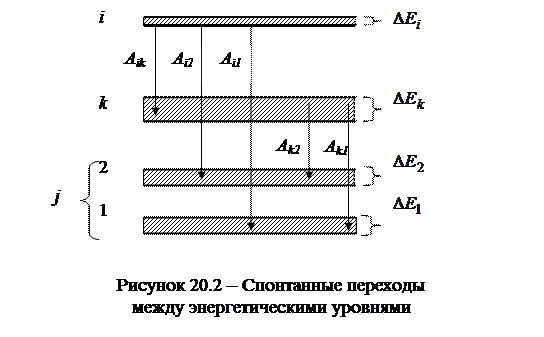
Значение времени жизни атома (молекулы) на энергетическом уровне, которое связано с изменением состояния в результате излучательного перехода, определяется коэффициентами Эйнштейна. Реальная схема энергетических уровней атомной системы содержит большое число уровней энергии. При этом время жизни на -ом энергетическом уровне определяется суммой вероятностей спонтанных переходов с рассматриваемого -го на все нижележащие 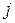-ые энергетические уровни (рисунок 20.2). Аналогичные рассуждения можно провести и для 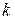-го энергетического уровня. Таким образом, время жизни атома (молекулы) на рассматриваемых уровнях можно представить следующим образом:

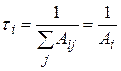и . (20.20)

Тогда естественную ширину -го энергетического уровня с учетом (20.19) можно выразить следующим образом:

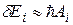. (20.21)

Естественную ширина спектральной линии, обусловленной квантовыми переходами между -ым и 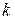-ым уровнями, с учетом формул (19.19) – (19.21) определим следующим образом:

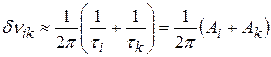. (20.22)

Таким образом, при квантовомеханическом описании естественная ширина спектральной линии определяется суммой вероятностей спонтанных излучательных переходов атома (молекулы), могущих произойти из исходного и конечного состояний за единицу времени.

В приведенном выше квантово-механическом описании вскрывается физическая природа естественного уширения спектральных линий, но невозможно описать их контур. Эта задача успешно решается на основе и квантовых, и классических представлений. Функция, посредством которой описывается спектральное распределение энергии, излучаемой в единицу времени классическим затухающим осциллятором:

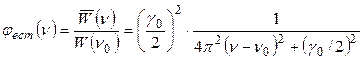. (20.23)

В формуле (20.23) φ_ест(v) – относительная интенсивность излучения, W(v₀) – максимальное значение спектральной плотности энергии осциллятора. Выражением (20.23) описывается естественный контур спектральной линии, называемый также дисперсионным или лорентцовским контуром. Схематически он представлен на рисунке 20.3.

В квантовой электродинамике доказывается, что контур линии при этом описывается формулой, совпадающей по виду с формулой (20.23), полученной в классической физике; при этом в (20.23) вместо 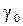следует ввести величину 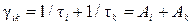. Таким образом,

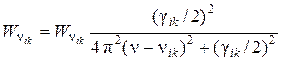. (20.24)

Анализируя формулу (20.23), легко показать, что полуширина спектральной линии, оцениваемая как разность частот, при которых относительная спектральная интенсивность составляет половину от максимального ее значения, δν_1/2 определяется по формуле:

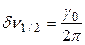, (20.25)

где 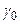– постоянная затухания, которая может быть приведена в соответствие с вероятностью спонтанного излучения, а именно: .

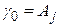Как показано в результате численных оценок, расчетные значения естественной ширины спектральных линий существенно меньше наблюдаемых на практике. Указанное несоответствие объясняется наличием других причин уширения спектральных линий – связанных с тепловым движением и столкновением частиц, а также обусловленных их взаимодействием и воздействием электрических и магнитных полей.

Рассмотрим основные факторы, обусловливающие уширение спектральных линий и полос в газах, дополнительное к естественному уширению.

Допплеровское уширение. Сущность допплеровского уширения заключается в зависимости частоты поглощаемого или испускаемого частицей излучения от скорости их поступательного движения. Если частица движется со скоростью 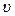под углом 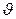к направлению распространения излучения, то доплеровское изменение частоты определяется следующим образом:

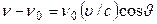, (20.26)

где v₀ – частота излучения неподвижного атома (молекулы).

Движение частиц имеет хаотический характер, и при тепловом равновесии в системе их распределение по скоростям определяется законом Максвелла – Больцмана. С учетом этого закона получено следующее выражение для относительного распределения интенсивности в пределах спектральной полосы:

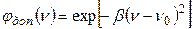, (20.27)

где

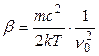. (20.28)

В формуле (20.28) m – масса частицы, k – постоянная Больцмана, Т – температура, выраженная в единицах абсолютной шкалы температур.

Воспользовавшись формулами (20.27) и (20.28) можно получить для полуширины допплеровского контура следующее выражение:

. (20.29)

Как показано в результате численных оценок, при обычных условиях ширина допплеровского контура на несколько порядков превосходит естественную ширину спектральной линии.

Ударное уширение. Продолжительность временного интервала, в течение которого возбужденный атом (молекула) излучает энергию, меньше естественного времени жизни вследствие его (её) взаимодействия с другими атомами (молекулами). Сущность ударного уширения состоит в том, что частица может осуществлять квантовый переход с -го энергетического уровня на нижележащие энергетические уровни не только испуская спонтанное излучение, но и результате соударения с другой частицей. Обозначим символами 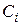вероятность безызлучательного квантового перехода частицы, обусловленного соударениями. Тогда, учитывая формулу (20.21), ширину -го уровня энергии, можно представить следующим образом:

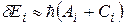, (20.30)

откуда для ширины спектральной линии получим:

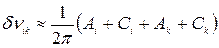. (20.31)

Рассматриваемое явление качественно аналогично интерпретируют и в классической теории. Наиболее простое выражение для контура спектральной линии, обусловленного столкновениями, имеет вид:

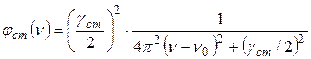. (20.32)

Видим, что формула (20.32) описывает лорентцовский контур спектральной линии, имеющий место при естественном уширении (20.23), с той лишь разницей, что постоянная затухания 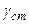здесь имеет иной смысл. В рамках газокинетических представлений применительно к столкновениям одинаковых частиц постоянная затухания определяется по формуле

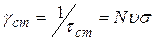, (20.33)

где 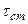– среднее время между столкновениями (среднее время свободного пробега), N – число молекул в единице объема, 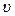– средняя скорость, – эффективное сечение соударений.

В результате числовых расчетов показано, что при обычных условиях полуширина ударного контура также превосходит естественную полуширину спектральной линии на несколько порядков.

Реальный контур индивидуальных спектральных линий частиц вещества, находящегося в газообразном состоянии, формируется в результате наложения доплеровского и ударного контуров. В частных ситуациях может оказаться преобладающей одна из этих причин уширения. Так, например, при низких давлениях и высоких температурах форма спектральных линий легких частиц является практически допплеровской, а при высоких давлениях основное значение, как правило, имеет ударное уширение. В зависимости от типа уширения реальный контур спектральной линии получается симметричным (так называемый дисперсионный контур, характерный для радиационного уширения) или асимметричным.

Дополнительное уширение спектральных линий может быть обусловлено конфигурационным взаимодействием частиц (эффект Яна – Теллера), воздействием электрических (эффект Штарка) и магнитных полей (эффект Зеемана), спин-орбитальным взаимодействием (мультиплетное расщепление), Ван-дер-Ваальсовым взаимодействием и др.

Date: 2015-05-19; view: 437; Нарушение авторских прав