
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Примерные задания
|
|
Аудиторная контрольная работа.
Темы: 1) Вычисление комбинаторных чисел, решение комбинаторных задач; 2) классическое определение вероятности; 3) формулы сложения и умножения вероятностей, 4) формулы полной вероятности и Байеса; 5) формула Бернулли; 6) дискретные случайные величины, законы их распределения и числовые характеристики; 7) непрерывные случайные величины, законы их распределения и числовые характеристики; 8) основные законы распределения случайных величин; свойства математического ожидания и дисперсии; 9) среднее арифметическое и дисперсия выборки; 10) мода, медиана, объём, графическое представление выборки.
ПРИМЕРНЫЕ ЗАДАНИЯ.
| №п/п | Задания | Ответы | ||||||||||
| 1.1 | Соответствие комбинаторного числа его значению:
1: 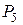 2: 2: 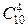 3: 3: 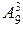 1:
1: 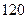 2: 2: 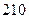 3: 3: 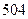 В ответе указать пары, соответствующих друг другу комбинаторных чисел и их значений.
В ответе указать пары, соответствующих друг другу комбинаторных чисел и их значений.
| 1-1 2-2 3-3 | ||||||||||
| 1.2 | В урне 5 чёрных и 6 белых шаров. Наудачу вынимают 4 шара. Тогда число способов отбора, при котором среди четырёх выбранных окажется два белых шара, равно:
1) 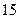 2) 2) 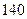 3) 3) 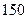 4) 4) 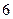 5) 5) 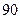
| 3) | ||||||||||
| 2.1 | Наудачу выбрано двузначное число. Тогда вероятность того, что выбранное число простое (делится нацело только на единицу и на себя) и сумма его цифр – пять, равна:
1) 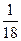 2) 2) 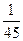 3) 3) 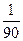 4) 4)  5) 5) 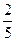
| 2) | ||||||||||
| 2.2 | В урне два белых, три чёрных и пять красных шаров. Наудачу вынимают три шара. Тогда по классическому определению вероятность того, что все вынутые шары одного цвета, равна 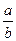 , где , где 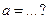 , , 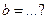 ( (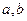 - целые числа).
Ответ представить в виде несократимой дроби: - целые числа).
Ответ представить в виде несократимой дроби: 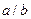
| 11/120 | ||||||||||
| 3. | На сессии студенту предстоит сдать экзамены по трём дисциплинам. Студент освоил 60% вопросов по первой дисциплине, 75% по второй и 65% по третьей. Тогда вероятность (по формулам сложения и умножения) того, что студент успешно сдаст хотя бы один экзамен, равна 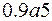 , где цифра , где цифра 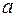 равна…
Записать ответ. равна…
Записать ответ.
| |||||||||||
| 4.1 | Вероятность того, что новый товар будет пользоваться спросом на рынке, если конкурент не выпустит в продажу аналогичный товар, равна 0.75, а при наличии конкурирующего товара равна 0.25. Вероятность выпуска конкурентом товара равна 0.35. Найти, используя формулу полной вероятности, вероятность того, что новый товар будет пользоваться спросом. Записать ответ. | 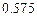
| ||||||||||
| 4.2 | Три станка-автомата производят однотипную продукцию, поступающую на сборочное производство в пропорции 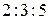 . Известно, что средний процент брака для первого станка равен 2%, для второго – 3% и для третьего – 1%. Выбранная наудачу деталь оказалась бракованной. Тогда вероятность по формуле Байеса того, что данная деталь изготовлена на втором станке, равна . Известно, что средний процент брака для первого станка равен 2%, для второго – 3% и для третьего – 1%. Выбранная наудачу деталь оказалась бракованной. Тогда вероятность по формуле Байеса того, что данная деталь изготовлена на втором станке, равна 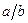 , где , где 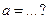 , , 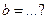 ( (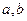 - целые числа).
Ответ представить в виде несократимой дроби: - целые числа).
Ответ представить в виде несократимой дроби: 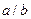
| 1/2 | ||||||||||
| 5.1 | В мастерской имеется 4 мотора. При существующем режиме работы вероятность того, что мотор в данный момент работает с полной нагрузкой равна 0.8. Найти, используя формулу Бернулли, вероятность того, что в данный момент более половины из них работает с полной нагрузкой. Записать ответ. | 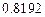
| ||||||||||
| 5.2 | Игральную кость бросают 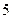 раз. Тогда вероятность того, что при этом число очков меньшее 5 появится менее двух или более четырёх раз, равна:
1) раз. Тогда вероятность того, что при этом число очков меньшее 5 появится менее двух или более четырёх раз, равна:
1) 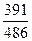 2) 2) 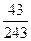 3) 3) 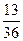 4) 4) 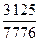 5) 5) 
| 2) | ||||||||||
| 6.1 | Дискретная случайная величина 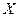 распределена по закону, заданному таблицей распределена по закону, заданному таблицей 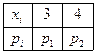 . Известно, что её математическое ожидание . Известно, что её математическое ожидание 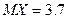 . Тогда вероятности . Тогда вероятности 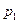 и и 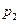 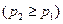 равны:
1) равны:
1) 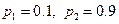 2) 2) 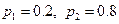 3) 3) 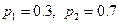 4)
4)  5) 5) 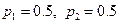
| 3) | ||||||||||
| 6.2 | Дискретная случайная величина 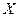 распределена по закону, заданному таблицей распределена по закону, заданному таблицей 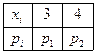 . Известно, что её дисперсия . Известно, что её дисперсия 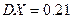 . Тогда вероятности . Тогда вероятности 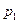 и и 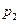 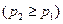 равны:
1) равны:
1) 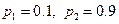 2) 2) 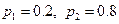 3) 3) 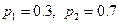 4)
4)  5) 5) 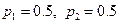
| 3) | ||||||||||
| 6.3 | В партии из 6 деталей содержится 4 стандартных. Дискретная случайная величина 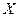 - число стандартных деталей среди трёх отобранных. Тогда её математическое ожидание - число стандартных деталей среди трёх отобранных. Тогда её математическое ожидание 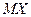 равно равно 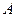 , где , где 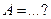 ( (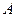 - целое число).
Вычисления проводить в дробях. Ответ представить в виде: - целое число).
Вычисления проводить в дробях. Ответ представить в виде: 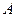
| |||||||||||
| 7.1 | Функция плотности распределения случайной величины 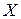 имеет вид имеет вид 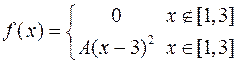 . Тогда постоянная . Тогда постоянная 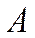 должна быть равна должна быть равна 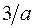 , где , где 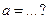 ( (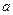 - целое число). Ответ представить в виде: - целое число). Ответ представить в виде: 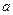
| |||||||||||
| 7.2 | Функция распределения непрерывной случайной величины 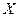 имеет вид имеет вид 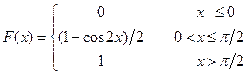 . Тогда её математическое ожидание . Тогда её математическое ожидание 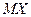 равно равно 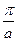 , где , где 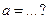 ( (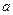 - целое число). Ответ представить в виде: - целое число). Ответ представить в виде: 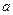
| |||||||||||
| 8.1 | Известны дисперсии независимых случайных величин 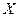 и и 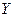 : : 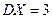 , , 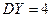 . Тогда дисперсия . Тогда дисперсия 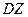 случайной величины случайной величины  равна:
1) равна:
1) 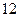 2) 2) 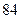 3) 3) 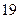 4) 4) 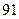 5) 5) 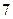
| 2) | ||||||||||
| 8.2 | Известны математические ожидания случайных величин 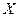 и и 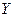 : : 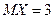 , , 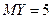 . Тогда математическое ожидание . Тогда математическое ожидание 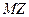 случайной величины случайной величины 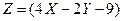 равно… Записать ответ. равно… Записать ответ.
| -7 | ||||||||||
| 8.3 | Случайная величина 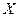 имеет нормальный закон распределения, заданный функцией плотности имеет нормальный закон распределения, заданный функцией плотности 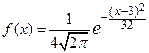 .Тогда дисперсия .Тогда дисперсия 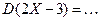 Записать ответ.
Записать ответ.
| |||||||||||
| 8.4 | Непрерывная случайная величина равномерно распределена на отрезке 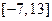 . Тогда вероятность . Тогда вероятность 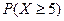 равна равна 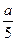 , где , где 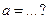 ( (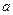 - целое число).
Вычисления проводить в дробях. Ответ представить в виде: - целое число).
Вычисления проводить в дробях. Ответ представить в виде: 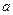
| |||||||||||
| 8.5 | Вероятность того, что при трёх выстрелах стрелок попадёт в цель хотя бы один раз, равна  . Дискретная случайная величина . Дискретная случайная величина 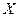 - число попаданий в цель при 20 выстрелах, имеет биномиальное распределение. Тогда её дисперсия - число попаданий в цель при 20 выстрелах, имеет биномиальное распределение. Тогда её дисперсия 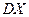 равна равна 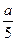 , где , где 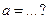 ( (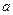 - целое число).
Вычисления проводить в дробях. Ответ представить в виде: - целое число).
Вычисления проводить в дробях. Ответ представить в виде: 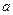
| |||||||||||
| 8.6 | Случайная величина 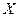 имеет показательный закон распределения, заданный функцией плотности имеет показательный закон распределения, заданный функцией плотности 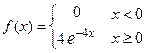 . Тогда дисперсия . Тогда дисперсия 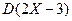 равна равна 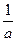 , где , где 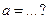 ( (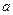 - целое число). Ответ представить в виде: - целое число). Ответ представить в виде: 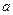
| |||||||||||
| 9. | Дано статистическое распределение выборки объёма 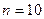 : :
Тогда среднее арифметическое выборки | 1) 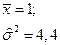
| ||||||||||
| 10.1 | Мода 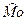 выборки: выборки: 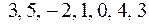 равна… Записать ответ. равна… Записать ответ.
| |||||||||||
| 10.2 | Дана выборка объёма 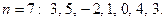 Тогда медиана выборки Тогда медиана выборки 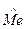 равна… Записать ответ. равна… Записать ответ.
| |||||||||||
| 10.3 | Из генеральной совокупности извлечена выборка объёма 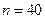 , полигон частот которой имеет вид: , полигон частот которой имеет вид:
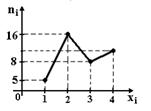 Тогда число вариант
Тогда число вариант 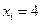 в выборке равно… Записать ответ. в выборке равно… Записать ответ.
| 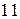
| ||||||||||
| 10.4 | По выборке объема n=100 построена гистограмма частот: 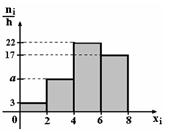 Тогда значение а равно:
1)
Тогда значение а равно:
1) 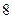 2) 2) 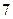 3) 3) 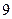 4) 4) 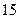 5) 5) 
| 1) |
| <== предыдущая | | | следующая ==> |
| Задание 6. Установить соответствие между определением метода научного познания и самим методом: | | | Противников церковных реформ патриарха Никона называли |
Date: 2015-05-18; view: 1012; Нарушение авторских прав
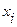
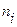
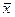 и дисперсия выборки
и дисперсия выборки 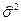 равны:
равны: