
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Приклади розв’язання задач
|
|
Задача №1. Яку потужність треба підводити до свинцевої кульки радіусом 4 см, щоб підтримувати її температуру 270С, якщо температура навколишнього середовища – 230С? Вважати, що тепло витрачається тільки внаслідок випромінювання. Поглинальна здатність свинцю дорівнює 0,6.
Розв’язання.
Переведемо числові дані в одиниці системи СІ:
r = 4 см = 0,04 м; Т = (273+27) =300К; Т0=(273-23) = 250К;
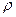 = 0,6
= 0,6
За законом Стефана –Больцмана, енергетична світимість абсолютно чорного тіла Re=  T4. З поверхні кульки S= 4
T4. З поверхні кульки S= 4 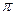 r2 випромінюється тепловий потік Фе=S
r2 випромінюється тепловий потік Фе=S  T4. Але оскільки випромінювання відбувається в середовищі з температурою Т0, то куля одночасно й поглинає потік випромінювання Ф0= S
T4. Але оскільки випромінювання відбувається в середовищі з температурою Т0, то куля одночасно й поглинає потік випромінювання Ф0= S  T4. Результуючий потік випромінювання
T4. Результуючий потік випромінювання
Ф1=Фе – Ф0 = S  (T4-T40) = 4
(T4-T40) = 4 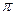 r2
r2 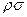 (T4-T40)
(T4-T40)
З урахуванням поглинальної здатності кулі
Р = Ф1 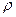 = S
= S 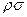 (T4-T40) = 4
(T4-T40) = 4 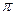 r2
r2 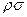 (T4-T40)
(T4-T40)
Обчислення Р = 4  3,14
3,14  16
16 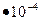 м2
м2  5,67
5,67  Вт м-2
Вт м-2 
К-4(3002 К4 – 2502 К4)  0,6 = 2,86 Вт
0,6 = 2,86 Вт
Задача №2. У скільки разів збільшиться потік випромінювання чорного тіла, якщо максимум енергії випромінювання пересунеться від червоної межі видимого спектра до його фіолетової межі?
Розв’язання.
Довжину хвилі, на яку припадає максимум енергії випромінювання чорного тіла, визначаємо із закону Віна
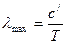 (1)
(1)
За формулою (1) визначаємо температури, які відповідають червоній (Тч) і фіолетовий (Тф) межам:
невизначеностей оцінити мінімальні розміри атома.
1.141.Використовуючи співвідношення невизначеностей у формі ΔхΔp≥ћ, оцінити мінімально можливу повну енергію електрона в атомі водню. Невизначеність координати дорівнює радіусу атома. Порівняйте отриманий результат з теорією Бору.
1.142.Скориставшись співвідношенням невизначеностей, оцінити розмитість енергетичного рівня в атомі водню 1) для основного стану; 2) для збудженого стану (час життя дорівнює 10-8 с).
1.143. Довжина хвилі випромінюваного атомом фотона складає λ=0,6 мкм. Приймаючи час життя збудженого стану Δt=10-8с, визначити відношення природної ширини енергетичного рівня, на який був збуджений електрон, до енергії, що випромінює атомом.
1.144. Визначити густину ядерної речовини, що виражається числом нуклонів в 1 см3, Якщо в ядрі з масовим числом А всі нуклони щільно упаковані в межах його радіусу.
1.145. Визначити енергію зв'язку атома гелію 2Не4. Маса нейтрального атома гелію дорівнює 6,6467 ·10-27кг.
1.146. Визначити питому енергію зв'язку (енергію віднесену до одного нуклона) для ядер: 1)2Не4. 2)6С12 Маса нейтральних атомів гелію і вуглецю дорівнює 6,6467 · 10-27 кг і 19,9272·10-27 кг.
1.147. Визначити масу ізотопу 7N15, якщо зміна маси при утворенні ядра 7N15 складає 0,2058·10-27 кг
1.148. Енергія зв'язку Езв ядра, що складається з трьох протонів і чотирьох нейтронів, дорівнює 39,3 МеВ. Визначити масу нейтрального атома, що має це ядро.
1.149. Визначити, що (і в скільки разів) довше - три періоди напіврозпаду або два середні часи життя радіоактивного ядра.
1.150. Визначити в скільки разів початкова кількість ядер радіоактивного ізотопу зменшиться за три роки, якщо за
1.132. Електронний пучок прискорюється в електронно-променевій трубці різницею потенціалів U =1кВ. Відомо, що невизначеність швидкості складає 0,1% від її числового значення. Визначити невизначеність координати електрона.
1.133.Використовуючи співвідношення невизначеностей, знайти вираз, що дозволяє оцінити мінімальну енергію електрона, що знаходиться в одновимірному потенційному нескінченно глибокому ящику шириною l.
1.134.Визначити відношення невизначеностей швидкості електрона якщо його координата встановлена з точністю до 10-5 м, і порошинки масою m=1012кг, якщо її координата встановлена з такою ж точністю.
1.135.Використовуючи співвідношення невизначеностей Гейзенберга, показати, що ядра атомів не можуть містити електронів. Вважати радіус ядра 10-15 м.
1.136. Електронний пучок виходить з електронної гармати під дією різниці потенціалів U =200В Визначити, чи можна одночасно змінити траєкторію електрона з точністю до 100 пм (з точністю порядку діаметру атома) і його швидкості з точністю до 10%
1.137. Електрон рухається в атомі водню по першій борівської орбіти. Приймаючи, що невизначеність швидкості, що допускається, складає 10% від її числового значення, визначити невизначеність координати електрона.
1.138. Слід пучка електронів на екрані електронно-променевої трубки має діаметр d = 0,5 мм. Відстань від електронної гармати до екрану l =20см, прискорююча напруга U =10кВ. Оцінити з допомогою співвідношення невизначеностей координати електрона на екрані.
1.139.Оцінити за допомогою співвідношення невизначеностей мінімально можливу енергію електрона в атомі водню і відповідну ефективну відстань його від ядра.
1.140. Кінетична енергія електрона в атомі водню дорівнює приблизно 10 еВ. Використовуючи співвідношення
видимої області спектра: Тч= с// 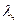 , Тф= с//
, Тф= с// 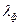
Потік випромінювання чорного тіла Фе=ReS, де
Re – енергетична світність чорного тіла; S – площа його поверхні. За законом Стефана- Больцмана, Rе=  T4. Отже,
T4. Отже,
Феч= S  T4ч, Феф= S
T4ч, Феф= S  T4ф, n =
T4ф, n = 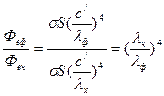

Задача 3. Визначити червоно хвильову межу фотоефекту для натрію, якщо робота виходу електрона з фотокатода дорівнює 2,3 еВ.
Розв’язання. Запишемо рівняння для червоної межі фотоефекту і обчислення з нього шукану довжину хвилі:

звідки
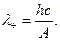
Обчислення:
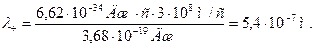
Задача 4.
Тиск монохроматичного світла з довжиною хвилі 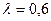 мкм на чорну поверхню
мкм на чорну поверхню
дорівнює 10-7 Н/м2. Скільки фотонів падає щосекунди на 1 м2 поверхні?
Розв’язання.
Тиск світла визначається за формулою
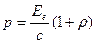 , де Ее=Фе/S – енергетична освітленість поверхні. Потік випромінювання Фе=
, де Ее=Фе/S – енергетична освітленість поверхні. Потік випромінювання Фе= 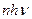 . Отже,
. Отже, 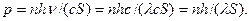 Звідси
Звідси 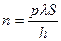
Обчислення: 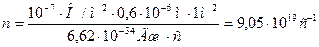 .
.
Задача 5. Визначити частоту світла, випромінюваного атомом водню, при переході електрона на рівень з головним квантовим числом і = 2, якщо радіус орбіти електрона змінився в 9 раз.
Розв’язання.
Частоту світла, випромінюваного атомом водню, визначають за формулою: 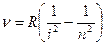 , де R – стала Ридберга; n – номер орбіти, з якої переходить електрон; і = 2 – номер орбіти, на яку переходить електрон.
, де R – стала Ридберга; n – номер орбіти, з якої переходить електрон; і = 2 – номер орбіти, на яку переходить електрон.
З формули 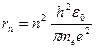 для радіуса орбіти випливає, що
для радіуса орбіти випливає, що 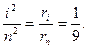
Поділимо і помножимо праву частину рівності (1) на і2; одержимо 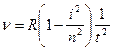 .
.
Обчислення: 
2,65·108 см/с. Враховуючи хвильові властивості електронів, визначити відстань між двома максимумами першого порядку в дифракційній картині, отриманій на екрані віддаленому, на L =10 см від щілини.
1.124. Знайти довжину хвилі де Бройля для атома водню, який рухається при температурі Т=293K з найбільш вірогідною швидкістю.
1.125. Розглядаючи електрон як класичну частинку, яка рухається у атомі водню по круговій орбіті довкола нерухомого протона, виразити швидкість v електрона і його механічну енергію W через радіус r орбіти.
1.126.Виходячи із спільної формули для фазової швидкості (vфаз = ω/к) визначити фазову швидкість хвилі де Бройля, яка вільно рухається із сталою швидкістю 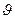 частинки в нерелятивістському і релятивістському випадках.
частинки в нерелятивістському і релятивістському випадках.
1.127.Електрон з кінетичною енергією T = 4эВ локалізований в області розміром l =1мкм. Оцінити за допомогою співвідношення невизначеностей відносну невизначеність його швидкості.
1.128.Визначити за допомогою співвідношення невизначеностей мінімальну кінетичну енергію електрона, який рухається усередині сферичної області діаметром d =0.1 нм.
1.129. Ширина сліду електрона (що має кінетичною енергією Т=1,5 кеВ) на фотопластині, отриманого за допомогою камери Вільсона, складає Δх =1мкм. Визначити, чи можливо по даному сліду виявити відхилення в русі електрона від законів класичної механіки.
1.130. Середня кінетична енергія в незбудженому атомі водню дорівнює 13,6еВ. Виходячи із співвідношення невизначеності, знайти найменшу неточність, з якою можна обчислити координату електрона в атомі.
1.131.Визначити відносну невизначеність імпульсу частинки, якщо допустити, що невизначеність її координати дорівнює довжині хвилі де Бройля.
d =0,15 нм. Визначити швидкість нейтронів, якщо брегівське відбивання першого порядку спостерігається, коли кут ковзання θ =300
1.114.Визначити, як зміниться довжина хвилі де Бройля електрона в атомі водню під час переходу його з четвертої борівської орбіти на другу.
1.115.Електрон, початковою швидкість якого можна знехтувати, минув прискорюючу різницю потенціалів U. Знайти довжину хвилі де Бройля для 2-х випадків: U1=51 В, U2=510 кВ.
1.116. Знайти довжину хвилі де Бройля для електрона, що має кінетичну енергію 1) Wk1 =10КэВ 2) Wk2 =1МэВ.
1.117.Заряджена частка прискорена різницею потенціалів U =200В має довжину хвилі де Бройля λ=2,02 нм. Знайти масу частки, якщо її заряд чисельно дорівнює заряду електрона.
1.118.Обчислити довжину хвилі де Бройля для протона, який рухається зі швидкістю 0,6с.
1.119. У досліді Девіссона і Джермера, що виявили дифракційну картину при відбиванні пучка електронів від природної дифракційної гратки монокристала нікелю, виявилось, що в напрямі, який становить кут α = 550 з напрямом падаючих електронів, спостерігається максимум відбивання четвертого порядку при кінетичній енергії електронів Т=180 еВ. Визначити відстань між кристалографічними площинами нікелю.
1.120.Знайти довжину хвилі де Бройля для електрона який рухається зі швидкістю V =2 108м/с.
1.121. Знайти довжину хвилі де Бройля для електрона, що має кінетичною енергією Т=3 еВ.
1.122. α-частинка рухається по колу радіусом R =8,3 мм в однорідному магнітному полі напруженість якого H=18,9кА/м. Знайти довжину хвилі де Бройля для частинки
1.123.На вузьку щілину шириною 1 мкм направлений паралельний пучок електронів, що мають швидкість
Задача 6. Визначити довжину хвилі де Бройля, якщо кінетична енергія електрона дорівнює 0,5 кеВ
Розв’язання.
Довжину хвилі де Бройля визначають за формулою  .
.
З виразу для кінетичної енергії  знайдемо
знайдемо 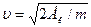 .
.
Підставивши 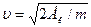 в
в  , дістанемо
, дістанемо
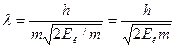 .
.
Обчислення: 
Задача 7. Обчислити дефект маси та енергію зв’язку ядра 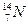 .
.
Розв’язання.
Дефект маси визначають за формулою 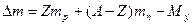 .
.
Цю формулу доцільно перетворити так, щоб до неї входила маса 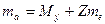 нейтрального атома, дефект маси якого визначається так:
нейтрального атома, дефект маси якого визначається так: 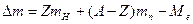 , де
, де 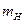 - маса нейтрального атома водню;
- маса нейтрального атома водню; 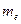 =0,00055а.о.м. – маса електрона.
=0,00055а.о.м. – маса електрона.
Обчислення: використавши табличні значення для ізотопу азоту 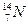 , знайдемо
, знайдемо
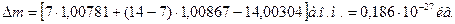
Енергія зв’язку ядра
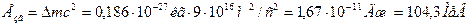 Задача 8. Виділяється чи поглинається енергія під час ядерної реакції
Задача 8. Виділяється чи поглинається енергія під час ядерної реакції
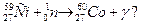 Обчислити цю енергію.
Обчислити цю енергію.
Розв’язання.
Для обчислення енергії ядерної реакції 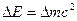 треба визначити дефект маси реакції
треба визначити дефект маси реакції 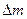 . Якщо
. Якщо 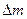 виражати в а.о.м., то
виражати в а.о.м., то 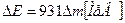 .
.
Дефект маси 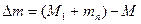 .
.
Оскільки число електронів до і після реакції зберігається, то замість значень мас ядер скористаємось значеннями мас нейтральних атомів:
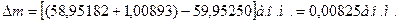
Реакція відбувається з виділенням енергії, оскільки 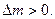
Обчислення: 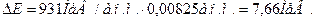
Задачі для самостійного розв’язання:
1.1. Є два абсолютно чорних джерела теплового випромінювання. Температура одного з них Т1=2500 К. Найти температуру іншого джерела, якщо довжина хвилі, що відповідає максимуму спектральної густини енергетичної світності на Δλ=0,5мкм більше довжини хвилі відповідній максимуму спектральної густини енергетичної світності першого джерела
1.2.Визначити енергію W, що випромінюється за час t =1 хв з оглядового віконця площею S=8 см2 плавильної печі, якщо її температура T=1,2кК
1.3. Визначити, у скільки разів необхідно зменшити термодинамічну температуру чорного тіла, щоб його енергетична світимість послабилась у 16 разів.
1.4. Температура внутрішньої поверхні муфельной печі при відкритому отворі площею 30 см2 дорівнює 1,3 кК. Приймаючи, що отвір печі випромінює як чорне тіло,
U =1В і 100В
1.104.Знайти довжину хвилі де Бройля для тих протонів, що пройшли прискорюючу різницю потенціалів U =1В і 100В.
1.105.Визначити довжину хвилі де Бройля для нейтрона, якій рухається з середньою квадратичною швидкістю при Т=290 К.
1.106.Дві однакові нерелятивістські частинки рухаються перпендикулярно одна одній з довжинами хвиль де Бройля λ1 і λ2 Знайти довжину хвилі де Бройля кожної частки в системі їх центру мас.
1.107. Заряджена частинка, що прискорена різницею потенціалів U =500 В, має довжину хвилі де Бройля λ =1,282 пм. Приймаючи заряд цієї частки рівним заряду електрона, визначити її масу.
1.108.Знайти довжину хвилі де Бройля для: 1) електрона який рухається із швидкістю V =10м/с 2) атома водню який рухається з середньою квадратичною швидкістю при температурі Т=300 K; 3) кульки масою m =1г, яка рухається з швидкістю V =1см/с.
1.109.Виведіть залежність між довжиною хвилі λ де Бройля релятивістською частинки і її кінетичної енергії.
1.110.Кінетична енергія електрона дорівнює 0,6 МеВ. Визначити довжину хвилі де Бройля.
1.111.Паралельний потік моноенергетичних електронів падає нормально на діафрагму з вузькою прямокутною щілиною шириною b =1мкм. Визначити швидкість цих електронів, якщо на екрані віддаленому від щілини на відстань l =50 см, ширина центрального дифракційного максимуму Δх = 0,36 мм.
1.112. Електрон рухається по колу радіусом 0.5 см в однорідному магнітному полі з індукцією 8·10-3 Тл. Визначити довжину хвилі де Бройля електрона.
1.113Моноенергетичний пучок нейтронів, що отримуються в результаті ядерної реакції, падає на кристал з періодом
довжиною хвилі λ=4,86·10-7м.
1.93. Використовуючи теорію Бору, визначити орбітальний магнітний момент електрона, який рухається по третій орбіті атома водню.
1.94. Визначити зміну орбітального механічного моменту електрона під час переходу його із збудженого стану в основний з випроміненим фотоном з довжиною хвилі λ=1,02·10-7м.
1.95.Позитроній - атомна система, що складається з позитрона і електрона, обертається щодо спільного центру мас. Застосовуючи теорію Бору, визначити мінімальні розміри подібної системи.
1.96.Визначити швидкість v електрона на третій орбіті атома водню.
1.97.Визначити циклічну частоту ω електрона на третій орбіті атома водню в теорії Бору.
1.98.Визначити частоту v електрона на першій орбіті атома водню і еквівалентний струм.
1.99.Визначити частоту світла, який випромінюється атомом водню, під час переходу електрона на рівень з головним квантовим числом n =2, якщо радіус орбіти електрона змінився в к = 9 разів.
1.100.Електрон вибитий з атома водню, що знаходиться в основному стані, фотоном енергія якого ε =17,7 еВ. Визначити швидкість електрона за межами атома.
1.101. Застосовуючи теорію Бору до мезоатома водню (у мезоатомі водню електрон замінений мюоном, заряд якого дорівнює заряду електрона, а маса в 207 разів більше маси електрона), визначити: 1) радіус першої орбіти мезоатома; 2) енергію іонізації мезоатома
1.102.Визначити імпульс і енергію 1) рентгенівського фотона 2) електрона, якщо довжина хвилі того і іншого дорівнює 10-10м.
1.103. Знайти довжину хвилі де Бройля для тих електронів, що пройшли прискорюючи різницю потенціалів
визначити, яка частина потужності розсіюється стінками, якщо споживана піччю потужність складає 1,5кВт
1.5. Визначити, як і у скільки разів зміниться потужність випромінювання чорного тіла, якщо довжина хвилі, яка відповідає максимуму спектральної густини енергетичної світності, змінилася від λ1=720 нм до λ2=400 нм.
1.6 Площа, обмежена графіком спектральної густини енергетичної світності чорного тіла, при переході від температури до температури збільшилася в 5 разів. Визначити, як зміниться при цьому довжина хвилі, яка відповідає максимуму спектральної густини енергетичної світності абсолютно чорного тіла.
1.7. У результаті нагрівання чорного тіла довжина хвилі, яка відповідає максимуму спектральної густини енергетичної світності, змінилась від λ1=2,7 мкм до λ2=0,9мкм. Визначити, у скільки разів збільшилася: 1) енергетична світність тіла; 2) максимальна спектральна густина енергетичної світності тіла.
1.8.Визначити, яка довжина хвилі відповідає максимальній спектральній густині енергетичної світності, яка дорівнює 1,3·1011 Вт/м2
1.9. Вважаючи нікель за абсолютно чорне тіло, визначити потужність, необхідну для підтримки температури розплавленого нікелю 1453 0С незмінною, якщо площа його поверхні дорівнює 0,5 см2. Втратами енергії знехтувати.
1.10. Металева поверхня площиною S =15см2, нагріта до температури T =3кК, випромінює в одну хвилину 100 кДж енергії. Визначити: 1) енергію що випромінює ця поверхня, вважаючи її чорною; 2) відношення енергетичних світностей цієї поверхні і чорного тіла при даній температурі.
1.11. Приймаючи Сонце за чорне тіло і враховуючи, що його максимальній спектральній густині енергетичної світності відповідає довжина хвилі 500 нм, визначити: 1)
температуру поверхні Сонця; 2) енергію, яку випромінює Сонце у вигляді електромагнітних хвиль за 10хв; 3) масу, що витрачається Сонцем за цей час за рахунок випромінювання.
1.12. У скільки разів треба збільшити термодинамічну температуру чорного тіла, щоб його енергетична світність R e збільшилась удвічі?
1.13 Температура верхніх шарів Сонця дорівнює 5300 К. Вважаючи Сонце за абсолютно чорне тіло, визначити довжину хвилі λm, на яку припадає максимум спектральної густини енергетичної світності Сонця
1.14 Випромінювання Сонця за своїм спектральним складом близьке до випромінювання абсолютно чорного тіла, знайти максимум спектральної густини енергетичної світності, який припадає на довжину хвилі λ=0,48 мкм. Знайти масу, що втрачається Сонцем щомиті за рахунок цього випромінювання. Оцінити час, за який маса Сонця зменшиться на 1%.
1.15. Мідну кульку діаметру d =1,2 см помістили у судину, температура стінок якої підтримується близькою до абсолютного нулю. Початкова температура кульки Т0 = 300 К. Враховуючи, що поверхня кульки є абсолютно чорною, знайти, через який час її температура зменшиться в η= 2 рази.
1.16.Температура поверхні Сонця Т0 = 5500 К. Вважаючи, що поглинальна здатність Сонця і Землі дорівнює одиниці і що Земля знаходиться в стані теплової рівноваги, оцінити її температуру.
1.17.Порожнина об'ємом V =1,0 л заповнена тепловим випромінюванням при температурі Т =1000 К. Знайти: а) теплоємність Cv; б) ентропію S цього випромінювання.
1.18.Визначити температуру тіла, яке при температурі навколишнього середовища t0 =230 С випромінювало би енергії більше в 10 разів чим поглинало.
довжину хвилі лінії серії Пальмера.
1.85.Частинка масою m рухається по колу в центрально-симетричному полі, де її потенціальна енергія залежить від відстані r до центру поля як U=kr2/2, к - позитивна стала. Знайти за допомоги борівської умови квантування, можливі радіуси орбіт і значення повної енергії частинки в даному полі.
1.86.Визначити довжину хвилі, яка відповідає: 1) границі серії Лаймана, 2), границі серії Бальмера 3) границі серії Пашена. Проаналізувати результати.
1.87.Визначити довжину хвилі спектральної лінії, яка відповідає переходу електрона в атомі водню з шостої орбіти на другу. До якої серії відноситься ця лінія і яка вона за рахунком?
1.88.Визначити ω - циклічну частоту обертання електрона на n - ой круговій орбіті водородоподобного іона. Обчислити цю величину іона Не+ при n = 2.
1.89. Атом водню знаходитися у збудженому стані, що характеризується головним квантовим числом n =4. Визначити можливі спектральні лінії в спектрі водню, що з'являються під час переходу атома із збудженого стану в основний.
1.90. На дифракційну гратку з періодом d нормально падає пучок світла від розрядної трубки, наповненої атомарним воднем. Виявилось, що в спектрі дифракційний максимум к -го порядку, спостерігається під кутом φ, і відповідає одній з серії Лаймана. Визначити головне квантове число, яке відповідає енергетичному рівню, з якого стався перехід.
1.91.Використовуючи теорію Бору для атома водню, визначити: 1) радіус найближчої до ядра орбіти (перший борівський радіус), 2) швидкість руху електрона по цій орбіті.
1.92.Визначити, на скільки зміниться енергія електрона в атомі водню при випромінюванні атомом фотона з
від Сонця, як і Земля. Яку масу повинна мати частинка в кометному хвості, поміщена на цій відстані, щоб сила світлового тиску на неї врівноважувалася силою тяжіння частинки Сонцем?
1.76. Рентгенівські промені з довжиною λ0=70,8 пм випробовують комптонівське розсіяння на парафіні. Знайти довжину хвилі рентгенівських променів, розсіяних в напрямах: 1)φ=π/2 2)φ=π.
1.77. Якою була довжина хвилі рентгенівського випромінювання, якщо при комптонівському розсіянні цього випромінювання графітом під кутом φ=600 довжина хвилі розсіяного випромінювання дорівнює λ=25,4 пм?
1.78.Фотон розсіявся під кутом θ=120° на вільному електроні, внаслідок чого електрон отримав кінетичну енергію Т= 0,45 МеВ. Знайти енергію фотона до розсіяння.
1.79. Рентгенівські промені з довжиною хвилі λ0=20 пм випробовують комптонівське розсіювання під кутом φ=900. Знайти зміну довжини хвилі ∆λ рентгенівських променів при розсіянні, а також енергію і імпульс електрона віддачі.
1.80. При комптонівському розсіюванні енергія падаючого фотону розподіляється порівну між розсіяним фотоном і електроном віддачі. Кут розсіяння φ=900. Знайти енергію і імпульс розсіяного фотона.
1.81. Енергія рентгенівських променів W =0,6МtВ. Знайти енергію електрону віддачі, якщо довжина хвилі рентгенівських променів після комптонівського розсіяння змінилася на 20%.
1.82. Визначити енергію фотона, що випромінюється під час переходу електрона в атомі водню з третього енергетичного рівня на другий.
1.83.Визначити максимальну і мінімальну енергії фотона у видимій серії спектру водню (серії Бальмера).
1.84. Максимальна довжина хвилі спектральної водневої лінії серії Лаймана дорівнює λ=0,12 мкм. Передбачаючи, що стала Ридберга невідома, визначити максимальну
1.19.Вважаючи, що теплові витрати обумовлені тільки випромінюванням, визначити, яку потужність необхідно підводити до мідної кульки діаметром d =2см, щоб при температурі навколишнього середовища t0 =130C підтримувати її температуру t =170C. Прийміть поглинальну здатність міді AT =0,6.
1.20.Визначить силу струму, що протікає по вольфрамовому дроту діаметром d =0,8 мм, температура якого у вакуумі підтримується постійною і дорівнює Т =28000С. Поверхню дроту вважати за сіру з поглинальною здатністю AT =0,343. Питомий опір дроту при даній температурі ρ=0,92 Ом·см. Температура оточення дроту Т =170
1.21.Для вольфрамової нитки при температурі Т =3500К поглинальна здатність AT =0,35. Визначити радіаційну температуру нитки.
1.22.Використовуючи формулу Планка, визначити спектральну густину потоку випромінювання одиниці поверхні чорного тіла, що припадає на вузький інтервал довжин хвиль Δλ=5нм біля максимуму спектральної густини енергетичної світності, якщо температура чорного тіла Т=2500К.
1.23. Температура вольфрамової спіралі в електричній лампочці Т=2450К, потужність - 25 ват.. Відношення її енергетичної світності і світності абсолютно чорного тіла при даній температурі k = 0,3. Знайти площу S поверхні яка випромінює.
1.24.Потужність випромінювання абсолютно чорного тіла N=10кВт. Знайти площу поверхні тіла яка випромінює, якщо максимум спектральної густини його енергетичної світності припадає на довжину хвилі λ=700нм.
1.25.Тиск монохроматичного світла з довжиною хвилі λ=500 нм на зачорнену поверхню, розташовану перпендикулярно падаючим променям, дорівнює 0,12 мкПа..
Визначити число фотонів, які падають щомиті на 1 м поверхні
1.26. На ідеально відбиваючу поверхню площиною S =5 см2 за час t =3хв нормально падає монохроматичне світло, енергія якого W =9 Дж. Визначити: 1) енергію опромінення поверхні; 2) світловий тиск, що діє на поверхню
1.27. На поверхню падає нормально електромагнітне випромінювання з інтенсивністю І. Визначити тиск р випромінювання на поверхню в двох випадках: коли поверхня чорна (що поглинає абсолютно) і коли вона дзеркальна
1.28.Світло падає на дзеркальну поверхню. Визначити тиск р світла на цю поверхню, якщо інтенсивність випромінювання дорівнює І, а кут падіння α.
1.29. Визначити тиск світла на стінки електричної лампочки потужністю150 Вт, допускаючи, що вся споживана потужність йде на випромінювання і стінки лампочки відбивають 15 % падаючого на них світла. Вважати лампочку сферичною судиною радіусом 4 см
1.30. Знайти світловий тиск на стінки електричної лампи потужністю 100Вт. Колба лампи є сферичною радіусом r = 5см. Стінки лампи відбивають 4% і пропускають 6% падаючого на них світла. Вважати, що вся споживана потужність йде на випромінювання.
1.31. На поверхню площиною S =0,01 м2 за одиницю часу падає світлова енергія W =1,05 Дж/с. Знайти світловий тиск у випадках: коли поверхня повністю відбиває, повністю поглинає падаючі на неї промені
1.32.Монохроматичний пучок світла λ=490 нм,падаючи по нормалі до поверхні, чинить світловий тиск р =4,9 мкПа. Яке число фотонів падає в одиницю часу на одиницю площини цієї поверхні? Коефіцієнт відбиття світла ρ=0,25
1.33. Тиск світла з довжиною хвилі λ=500 нм на зачорнену поверхню, розташовану перпендикулярно падаючому випромінюванню, р =0,15мкПа. Визначити число фотонів.
рентгенівських фотонів з нерухомими вільними електронами. Врахувати, що при цій взаємодії електрони - набувають релятивістських швидкостей
1.69.Довжина хвилі рентгенівського випромінювання після комптонівського розсіяння збільшилася з λ1= 2,0 пм до λ2 - 2,4 пм. Визначити кінетичну енергію Wk електронів, що вилітають (виразіть її в МеВ) і їх швидкість v. Визначити також кут розсіяння θ рентгенівського випромінювання і кут α між - напрямом вильоту електронів і напрямом падаючого випромінювання.
1.70. Вузький пучок монохроматичного рентгенівського випромінювання падає на речовину, що його розсіює. Виявляється, що довжина хвиль розсіяного під кутами θ1=600 і θ2=1200 випромінювання відрізняються в 1,5 рази. Визначити довжину хвилі падаючого випромінювання, передбачаючи, що розсіювання відбувається на вільних електронах.
1.71. Фотон з довжиною хвилі λ = 6 пм розсіявся під прямим кутом на вільному електроні, що покоїться. Знайти: а) частоту розсіяного фотона; б) кінетичну енергію електрона віддачі.
1.72. Фотон з довжиною хвилі λ=5 пм випробував комптонівське розсіювання під кутом θ=900 на вільному електроні, що спочатку покоївся. Визначити: 1) зміну довжини хвилі при розсіюванні; 2) енергію електрона віддачі; 3) імпульс електрона віддача.
1.73.Фотон з енергією ћω=250 КеВ розсіявся під кутом θ=120° на вільному електроні, що спочатку покоївся. Визначити енергію розсіяного фотона.
1.74.Фотон з енергією ε=0,25 МеВ розсіюється на вільному електроні, що спочатку покоївся. Визначити кінетичну енергію електрона віддачі, якщо довжина хвилі розсіяного фотона змінилася на 20%.
1.75.Знайти світловий тиск сонячних променів на абсолютно чорне тіло, яке знаходиться на такій же відстані
де с - швидкість світла.
1.62. При почерговому освітленні поверхні деякого металу світлом з довжинами хвиль λ1= 0,35 мкм і λ2=0,54 мкм виявили, що відповідні максимальні швидкості фотоелектронів відрізняються один від одного в η = 2 рази. Знайти роботу виходу з поверхні цього металу.
1.63. Визначити мінімальну довжину хвилі в суцільному спектрі рентгенівських променів, якщо рентгенівська трубка працює під напругою U = 30 кВ.
1.64.На металеву пластину падає монохроматичне світло (λ = 0,413 мкм). Потік фотоелектронів з поверхні металу, повністю затримується, коли різниця потенціалів гальмівного електричного поля досягає U = 1,00 В. Визначити роботу виходу в электрон-вольтах і червону межу фотоефекту.
1.65. Визначити максимальну швидкість електронів, що вилітають з металу під дією γ -опромінення з довжиною хвилі λ = 0,030 А
1.66. Фотон з енергією ε = 1,025 МеВ розсіявся на вільному електроні, що спочатку покоївся. Визначити кут розсіювання фотона, якщо довжина хвилі розсіяного фотона дорівнює комптонівській довжині хвилі λ=2,43 пм
1.67. Визначити довжину хвилі λ електромагнітного випромінювання, якщо енергія одного кванта цього випромінювання дорівнює енергії спокою електрона. З якою швидкістю v повинен рухатися електрон, щоб його імпульс дорівнював імпульсу такого фотона? Визначити відношення енергії W рухомого електрона до енергії W γ фотона.
1.68. Рентгенівське випромінювання з довжиною хвилі λ, взаємодіючи з речовиною відклоняється від первинного напряму поширення на кут θ. При цьому довжина хвилі розсіяного випромінювання збільшується на Δλ (ефект Комптона). Виразити величину Δλ через кут θ, розглядаючи розсіяння як результат зіткнень
падаючих на поверхню площиною 40 см2 за одну секунду.
1.34. Тиск монохроматичного світла з довжиною хвилі λ=600 нм на зачорнену поверхню, розташовану перпендикулярно випромінюванню, складає 0,1 мкПа. Визначити: 1) концентрацію фотонів у світловому пучку; 2) число фотонів падаючих щосекунди на 1 м поверхні.
1.35. На ідеально відбиваючу поверхню нормально падає монохроматичне світло довжиною хвилі λ=0,55 мкм. Потік випромінювання Фе складає 0,45 Вт. Визначити: 1) число фотонів, падаючих на поверхню за час t =3 с; 2) силу тиску, що діє на цю поверхню.
1.36. Плоска світлова хвиля інтенсивністю І =0,1 Вт/см2 падає під кутом α=300 на плоску відбиваючу поверхню з коефіцієнтом відбивання ρ=0,7. Використовуючи квантові уявлення, визначити нормальний тиск, що створюється світлом на цю поверхню.
1.37. Знайти масу фотона 1) червоних променів λ=700нм; 2) рентгенівських променів λ=25пм; 3) гамма - променів λ=1,24 пм.
1.38. Знайти енергію і імпульс фотона, якщо відповідна йому довжина хвилі λ=1,6 пм.
1.39.Геліво-неоновий лазер працює в безперервному режимі, розвиваючи потужність Р = 2,0 мВт. Випромінювання лазера має довжину хвилі  = 630 нм. Скільки фотонів випромінює лазер за одну секунду?
= 630 нм. Скільки фотонів випромінює лазер за одну секунду?
1.40.Енергія кожного фотона в пучку монохроматичного випромінювання Wo = 4,4·10 -19 Дж. Яка довжина хвилі λ цього випромінювання у воді?
1.41. Під якою напругою U працює рентгенівська трубка, якщо «найжорсткіше» випромінювання в спектрі цієї трубки має довжину хвилі λmin= 3,0·10-11 м?
1.42. З якою швидкістю повинен рухатися електрон, щоб його кінетична енергія дорівнювала енергії фотона з довжиною хвилі λ=520 нм
1.43. Для калію червона межа фотоефекту λmax=0,62 мкм. Яку максимальну швидкість v можуть мати фотоелектрони, що вилітають при опромінюванні калію фіолетовим світлом з довжиною хвилі λ = 0,42 мкм?
1.44.Мінімальна частота світла, що вириває електрони з поверхні металевого катоду, v 0 = 6,0·1014Гц. При якій частоті v світла електрони, що вилетіли, повністю затримуються різницею потенціалів U = 3,0 В?
1.45.При освітленні поверхні деякого металу фіолетовим світлом з довжиною хвилі λ1=0,4 мкм вибиті світлом електрони повністю затримуються різницею потенціалів U1 = 2,0 В. Чому дорівнює затримуюча напруга U2 при освітленні того ж металу червоним світлом з довжиною хвилі λ2 = 0,77 мкм?
1.46 З якою швидкістю повинен рухатися електрон, щоб його імпульс дорівнював імпульсу фотона з довжиною хвилі λ=520 нм
1.47. Яку енергію ε повинен мати фотон, щоб його маса дорівнювала масі спокою електрона?
1.48.Імпульс, який переноситься монохроматичним пучком фотонів через площину S =2см2 за час t =0,5 хв., дорівнює р =3·10-9 кг·м/с. Знайти для цього пучка енергію Е, падаючу на одиницю площини за одиницю часу.
1.49. При який температурі Т кінетична енергія молекули двоатомного газу дорівнюватиме енергії фотона з довжиною хвилі λ=589 нм.
1.50. Знайти масу фотона, імпульс якого дорівнює імпульсу молекули водню при температурі Т =200С. Вважати, що швидкість молекули дорівнює середній квадратичній швидкості.
1.51.Знайти довжину хвилі світла, що відповідає червоній межі фотоефекту. Для літію, натрію, калія і цезію.
1.52. Довжина хвилі світла, що відповідає червоній межі фотоефекту для деякого металу λ=275 нм. Знайти мінімальну енергію того фотона, що спричиняє фотоефект.
1.53. Довжина хвилі світла, яка відповідає червоній межі фотоефекту, для деякого металу λ=275 нм. Знайти роботу виходу А електрона з металу, максимальну швидкість електронів, які вириваються з металу світлом з довжиною хвилі λ=180 нм, і максимальну кінетичну енергію Е електронів
1.54. Знайти частоту світла, що вириває з металу електрони, які повністю затримуються різницею потенціалів U =3В. Фотоефект стискується при частоті світла v0 =6·1014Гц. Знайти роботу виходу електрона з металу.
1.55. Визначити максимальну швидкість фотоелектронів, що вириваються з поверхні металу, якщо фотострум припиняється при подачі затримуючої напруги U0=3,7 В.
1.56.Червона межа фотоефекту для деякого металу дорівнює λ=500нм. Визначити значення енергії фотона, що спричиняє фотоефект.
1.57. Знайти затримуючу різницю потенціалів для електронів вирваних при освітленні калію світлом з довжиною хвилі λ=330 нм.
1.58. При фотоефекті з платинової поверхні, електрони повністю затримуються різницею потенціалів U =0,8 В. Знайти довжину хвилі опромінення і граничну довжину хвилі, при якій ще можливий фотоефект.
1.59. Фотони з енергією ε = 4,9 эВ виривають електрони з металу з роботою виходу А = 4,5 эВ. Знайти максимальний імпульс при вильоті кожного електрона
1.60.Точкове ізотропне джерело випромінює світло з λ = 589 нм. Світлова потужність джерела Р = 10 Вт. Знайти: а) середню густину потоку фотонів на відстані r = 2,0 м від джерела; б) відстань від джерела до точки, де середня концентрація фотонів n = 100 см-3.
1.61. Знайти довжину хвилі короткохвильової межі суцільного рентгенівського спектру, якщо швидкість електронів, що підлітають до антикатоду трубки, v = 0,85 с,
Date: 2015-05-18; view: 2469; Нарушение авторских прав