Состояния, энергия, энтропия

На Вселенную иногда смотрят как на скопление энергетических полей. Такой взгляд хорошо соответствует представлениям квантовой теории, в которой доказывается, что «все есть энергия», что энергия – это основная величина, определяющая состояние системы (любого размера, вплоть до Универсума), и, исходя из энергетической характеристики объекта, можно определить среднее значение других физических величин, характеризующих систему. Более того, квантовая теория сегодня способна количественно описать, как возникают все эти «скопления энергетических полей», как появляются локальные энергетические объекты с различной плотностью энергии, в том числе и наш плотный предметный мир, из нелокального квантового источника, в котором изначально нет никаких энергетических неоднородностей. Квантовая теория способна описывать как переходы объекта из менее плотного энергетического состояния в болееплотное, так и обратный процесс.

В квантовой механике нет таких проблем с понятием «энергия», как в классической физике, где нет четкого и однозначного ее определения. В квантовой теории эта величина вводится непосредственно из аксиоматики квантовой механики, исходя из основополагающего понятия «состояние». Каждому состоянию в квантовой теории соответствует определенное значение энергии, то есть энергия квантуется в соответствии с различными состояниями системы.

Можно сказать, что энергия в квантовой теории – это обобщение всех известных (и неизвестных) энергий в классической физике, и она связана лишь с состоянием системы. В квантовой теории просто не может быть никаких неизвестных энергий, поскольку в качестве энергии мы можем задать любую (разумную, подходящую) функцию состояния системы. Можно задать и целый набор таких функций, то есть рассматривать совокупность энергий тварного и нетварногомира. Любое изменение состояния системы, например, любая наша мысль, чувство, желание и т. п., с точки зрения квантовой теории, связаны с изменением ее энергии, поскольку последняя – это функция состояния системы, и если меняется состояние – меняется и энергия.

Понятие «состояние» в квантовой механике непосредственно не связано с привычными классическими характеристиками системы (массой, скоростью и т. д.). Эти величины вторичны, и для нелокальных состояний они просто неприменимы. Энергия в этом отношении – более универсальная величина, ее можно использовать во всех случаях. Для физических объектов (если мы не рассматриваем, например, в терминах квантовой теории текстовое сообщение) состояние системы может быть описано в терминах одной ее характеристики – энергии. Обычно предполагается, что энергия должна быть определена в некотором заданном интервале. Все наблюдаемые физические величины, в том числе классические, можно получить из матрицы плотности. В случае замкнутой системы матрица плотности записывается через вектор состояния в виде проектора. Таким образом, матрица плотности в энергетическом представлении (и вектор состояния для замкнутой системы) отражает реальное, объективное состояние системы с определенным энергетическим спектром.

В целом, можно сказать, что квантовая теория изучает физические законы, которым подчиняются любые энергетические структуры (независимо от их размера и типа энергии). В настоящее время квантовая механика приступила к изучению физических процессов, в результате которых энергетические структуры возникают из нелокального состояния и уплотняются (декогеренция), а также обратных процессов – разуплотнения энергетических структур, перехода их в менее плотное состояние (возрастание квантовой запутанности), вплоть до полного «растворения» и потери своей внутренней структуры – чистого нелокального состояния. Особо подчеркну, что это не просто теоретизирование. То, что эти процессы действительно существуют в окружающем мире, подтверждается многочисленными физическими экспериментами, которые показывают адекватное соответствие теоретическим предсказаниям. Более того, эти процессы применяются на практике в технических устройствах, о чем уже неоднократно упоминалось.

Квантовая теория информации устанавливает связь между мерой квантовой запутанности и информацией. Это позволяет рассмотреть декогеренцию как процесс перехода Слова в его осязаемую форму. В терминах Кастанеды это относится и к физическому процессу, при котором наша мысль, команда, точнее, наше «намерение» становится «командой Орла» и реализуется в плотном мире. Кроме того, связь между энергией и квантовой информацией дает возможность сделать еще один вывод: все энергетические процессы связаны с процессами информационными, и на фундаментальном уровне Универсума, в нелокальном (нетварном) источнике Реальности все энергетические процессы в подсистемах сводятся к информационным. На фундаментальном уровне нет ничего, кроме квантовой информации, которая в процессе декогеренции проявляется в пространствах меньшей размерности в виде локальных объектов и тварных энергий.

Поскольку термин «энергия» будет часто встречаться в последующих главах, я попытаюсь пояснить, что же подразумевается под этим понятием в контексте этой книги. Тем, кто желает более подробно узнать, как из самых простых соображений в квантовой теории вводится понятие «энергия», могу порекомендовать прочесть первые главы курса «Статистической термодинамики» Ч. Киттеля. Этот курс интересен тем, что вся термодинамика здесь очень легко и достаточно строго выводится из простейшей квантовомеханической модели из (не взаимодействующих!) элементарных магнитиков с двумя ориентациями магнитного момента (вверх/вниз).

Но для начала – несколько слов об основах квантового подхода к описанию макроскопических процессов.

Как пишет Киттель в предисловии*: «Статистическая термодинамика представляется удивительно легким предметом, если при ее изучении придерживаться последовательной квантовомеханической точки зрения, в основе которой лежит понятие состояний всей системы, независимо от того, велика она или мала».

* Киттель Ч. Статистическая термодинамика. М.: Наука, 1977. С. 9.

И далее, в начале первой главы: «В настоящее время мы знаем, что статистическую термодинамику легче изучать с позиций квантовой механики, чем на основе классической механики времен Гиббса. Это обстоятельство неудивительно, поскольку квантовая механика дает правильное описание природы, тогда как на атомном уровне описание в рамках классической механики является неполным. Только переведя принципы Гиббса на язык квантовой механики, мы приходим к ясному, последовательному и простому физическому обоснованию как термодинамики, так и статистической механики. В процессе такого перевода существенно использование только одного-единственного понятия квантовой механики, а именно – понятия о стационарном квантовом состоянии системы частиц».

В простейшей квантовомеханической модели из элементарных магнитиков состоя­ние системы определяется заданием ориентации (вверх или вниз) каждого из них. И энергия системы определяется достаточно просто, исходя из ее состояния. Энергия выражается через следующую разность, которая в данном случае называется спиновым избытком:

(число спинов вверх) – (число спинов вниз) = спиновый избыток.

Например, состояние, в котором число спинов «вверх» равно числу спинов «вниз», имеет нулевую энергию (равномерное распределение энергии). Два состояния, в котором все спины направлены вверх (вниз), имеют максимальную энергию из всех возможных для данной системы.

Таким образом, энергия системы – это величина, которая характеризует отклонение системы от равновесного состояния. Отсюда – связь с классической физикой и всевозможными определениями энергии, которые в ней используются. Все они в основе своей содержат квантовомеханическое определение энергии и с классической точки зрения характеризуют работу, которую может совершить система при ее переходе к равновесному состоянию. Здесь мы видим естественный переход к понятию силы (градиента энергии), который совершает эту работу.

Отмечу, что вся классическая термодинамика выводится из простейшей квантовомеханической модели невзаимодействующих спинов, и остается возможность дальнейшего совершенствования этой модели. Очевидным становится то основное упрощение, следствием которого являются законы классической термодинамики. Поскольку не учитываются взаимодействия между частицами, из рассмотрения убираются несепарабельные состояния и нелокальные квантовые корреляции.

Курс статистической термодинамики Киттеля хорош еще и тем, что он на конкрет­ном примере показывает высокую эффективность подхода квантовой механики к объяснению физических процессов в окружающей реальности. Замечу – любых процес­сов, в том числе макроскопических, поскольку в основеквантовомеханической точки зрения «лежит понятие состояний всей системы, независимо от того, велика она или мала».

Задать энергию как функцию состояния можно и без привязки к физике, а, скажем, для характеристики информационных процессов. К примеру, выразить ее через аналог «спинового избытка» (удобнее брать удвоенную разность между числом нулей и единиц в векторе состояния в двоичном базисе). Можно еще проще – как число единиц в векторе состояния. В частности, состояние из всех нулей |000...00ñ принять за минимальное значение энергии, тогда ортогональное ему состояние из всех единиц – состояние с максимальным значением энергии. А энергию для всех промежуточных состояний определять числом единиц, то есть энергия состояния |01100ñ равна 2, для состояния |10110ñ равна 3 и т. д. Здесь можно подумать о нормировке, о том, как удобнее ввести энергию, но суть остается – нужно как-то связать число нулей и единиц в векторе состояний с количественным значением энергии.

Такое определение энергии имеет и некоторый физический смысл: например, в случае передачи информации по каналу с шумом для «переворота» (искажения) одного символа требуется меньше энергии внешнего воздействия (шума), чем для «переворота» двух и более символов.

После этого можно говорить о градиенте энергии. Так, если есть два локальных объекта в исходном состоянии: |000...00ñ (один из них) и |111...11ñ – другой (каждое из этих состояний сепарабельное), и они приходят во взаимодействие, то градиент энергии между ними будет максимальный (перепад энергии максимально возможный, так как одна подсистема находится в состоянии с минимальной энергией, а другая – с максимально возможной энергией). Возникает поток энергии, который приводит всю систему в равновесие, и она перейдет, например, в суперпозиционное состояние 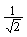(|000...00ñ + |111...11ñ) –несепарабельное, максимально запутанное и нелокальное. В квантовой теории оно называется кэт-состояние в память о шредингеровском коте, который находится в состоянии «ни жив, ни мертв».

Несколько слов об энтропии. Энтропия и энергия в физике неразрывно связаны друг с другом. При формальном определении энергии, скажем, как числа единиц в двоичном базисе можно эту связь установить для любых состояний (не только физических).

Энтропия по своему фундаментальному определению (в терминах состояний) – это логарифм от числа допустимых состояний системы.

Как говорит Киттель: «Это определение ошеломляет своей простотой: энтропия есть логарифм числа допустимых состояний системы. <...> Говорят, что энтропия служит мерой беспорядка в системе. Такое утверждение точно соответствует определению. Чем больше у системы допустимых состояний, тем больше энтропия».

Как известно, статистическая физика исходит из следующего основного предположения (иногда это утверждение называют основной гипотезой статистической физики): замкнутая система с равной вероятностью может находиться в любом допустимом для нее состоянии. Состояние считается допустимым, если оно удовлетворяет наложенным на систему ограничениям. Основные ограничения – это ограничения по энергии и по числу подсистем (определяется размерностью гильбертова пространства).

Число допустимых состояний, в свою очередь, зависит от энергии. Поясню этот момент на примере системы из 10 двухуровневых подсистем (в двоичном базисе). Для состояния с максимальной энергией, то есть 1111111111, есть только одно допустимое состояние. Для состояния с чуть меньшей энергией, например, с одним нулем – уже 10 допустимых состояний, скажем, 1101111111, то есть 10 различных вариантов размещения 0. Это степень вырождения для данного значения энергии. Для состояния с двумя нулями число допустимых состояний (степень вырождения) равно 45 и т. д. Максимальное число допустимых состояний (252) имеет место для состояний из 5 единиц и 5 нулей, то есть состояний типа 1101011000. Здесь работает комбинаторика, и в целом мы имеем гауссово распределение для числа допустимых состояний.

Таким образом, энтропия (логарифм от числа допустимых состояний)* является функцией энергии (числа единиц в нашем случае), то есть:

σ (m) = ln g (m),

где m – энергия (число единичек); g (m) – степень вырождения для данного значения энергии (число допустимых состояний, соответствующих этой энергии).

* Общепринятое термодинамическое определение энтропии отличается только наличием множителя k_b – постоянной Больцмана, равной 1,381 · 10^–16 эрг/К.

Минимальная энтропия будет равна нулю (одно состояние) для состояний 1111111111 и 0000000000 (для состояний с максимальной и минимальной энергией), а максимальное значение энтропии в нашем примере равно 5,53 (ln252).

Такая схема позволяет ввести формальное понятие энергии для любой нефизической системы, состояния которой заданы в двоичном базисе, и оно будет согласовано с понятием энтропии.

Можно также достаточно просто показать, почему при взаимодействиях (при обмене энергией) возникают суперпозиционные состояния и квантовая запутанность.

Согласно статистической физике, при взаимодействии двух подсистем энергия перераспределяется таким образом, чтобы объединенная система имела максимальное число допустимых состояний (энтропия была максимальна). Объединенная система стремится к равновесию, к наиболее вероятностной конфигурации (к вершине «колокола» на гауссовой кривой).

Суммарная энергия m = m ₁ + m ₂ при этом остается постоянной, а меняются значения энергии подсистем m ₁ и m ₂ (энергия перераспределяется). Обозначим эти новые значения m' ₁ и m' ₂. Система стремится к равновесному состоянию, при котором относительные энергии равны, то есть выполняется условие*

m' ₁/ N ₁ = m' ₂/ N ₂ = m / N,

где N ₁₍₂₎ и N – размерность подсистем и объединенной системы (число двоичных позиций), N = N ₁ + N ₂.

* См.: Киттель Ч. Статистическая термодинамика. М.: Наука, 1977. С. 44.

Например, пусть начинают взаимодействовать две подсистемы 00000 и 11111 с энергией m ₁ = 0 и m ₂ = 5, размерностью N ₁ = 5, N ₂ = 5, и образуется объединенная система размерностью N = 10 (как в нашем предыдущем примере). Мы будем иметь m / N = 1/2, то есть значения m' ₁ и m' ₂, согласно условию равновесия, должны быть равны 2,5, что невозможно реализовать без суперпозиционных состояний, то есть состояния каждой из наших подсистем должны быть равны 1/2(00000 + 11111), а это максимально-запутанное cat -состояние.

Можно даже предположить, что здесь справедлив и более общий вывод: при объединении двух систем (одинаковой размерности) с минимальной и максимальной энергией объединенная система стремится к максимально запутанному cat -состоянию.

В нашем примере «на бумаге» можно иногда обойтись без суперпозиции состояний, скажем, когда объединяются подсистемы четной размерности. Но условие равновесия должно работать во всех случаях, и без суперпозиции состояний здесь не обойтись – этот вариант работает всегда.

Такую общую схему, связывающую состояния и энергию, можно рассматривать в самых разных задачах, в том числе при количественном описании деятельности сознания. Наличие сознания неизменно связано со сменой внутреннего состояния системы, обладающей им. Всегда можно сопоставить ссознанием вектор состояния в некотором заданном базисе из эмоциональных и (или) ментальных собственных состояний и применять методы квантовой теории. Одновременно с этим сознание будет пониматься как элемент «энергетического мира», поскольку изменение состояния сопровождается изменением энергии системы. И что самое интересное – при таком подходе получается, что эти «психические выделения» энергии, сопровождающие деятельность сознания, являются объективно существующими «энергетическими сгустками». Это не есть что-то идеальное, существующее только в нашей голове, – это объективные энергетические потоки в окружающей нас реальности. Если мы соглашаемся с тем, что наше состояние при активной деятельности сознания изменяется, что из одного состояния мы переходим в другое, и одна мысль (эмоция) сменяет другую, то отсюда неизбежно следует вывод, что мы генерируем или поглощаем энергию, так как различным состояниям соответствуют разные энергии.

Таким образом, когда артисты, например, говорят об энергетике зрительского зала, то речь идет не о каких-то чисто субъективных внутренних переживаниях, а о вполне реальных физических процессах взаимодействия и обмена энергией, влияющих на состояние взаимодействующих субъектов. Естественно, что эти энергетические процессы не могут иметь место в рамках классической физики, но квантовая теория в состоянии их объяснить и количественно описать.

Date: 2015-05-18; view: 429; Нарушение авторских прав