Волны материи

Когда де Бройль примерно в 1924 г. писал свою кандидатскую диссертацию, он провел параллель между дискретностью стационарных орбит атома Бора и дискретностью звуковых волн, производимых гитарой. Параллель оказалась плодотворной.

Представьте себе движение звуковой волны в некоторой среде (рис. 4). Вертикальное смещение частиц среды меняется от ноля до максимума (гребень), обратно до ноля, до отрицательного максимума (впадины), опять до ноля, и так далее с увеличением расстояния. Максимальное вертикальное смещение в одном направлении (от ноля до гребня или впадины) называется амплитудой. Отдельные частицы среды движутся взад и вперед относительно своего покоящегося положения. Однако волна, проходящая через среду, распространяется. Волна представляет собой распространяющееся возмущение. Число гребней, проходящих через данную точку за секунду, называется частотой волны, а расстояние от гребня до гребня — длиной волны.

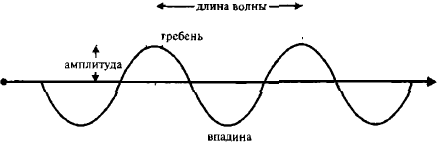
Рис. 4. Графическое представление волны

Щипок гитарной струны приводит ее в движение, но возникающие колебания называются стационарными (стоячими волнами), поскольку они не распространяются за пределы струны. В любом данном месте струны смещение частиц струны меняется во времени: имеет место волнистость, но волны не распространяются в пространстве (рис. 5). Распространяющиеся волны, которые мы слышим, приводятся в движение стоячими волнами колеблющихся струн.

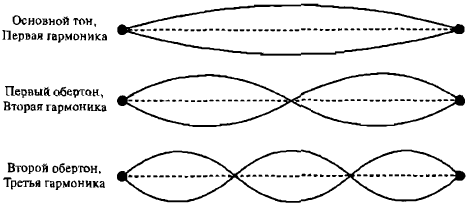
Рис. 5. Первые несколько гармоник стационарной, или стоячей, волны в гитарной струне

Музыкальная нота гитары состоит из целого ряда звуков — спектра частот. Де Бройля заинтересовало то, что стоячие волны гитарной струны создают дискретный спектр частот, называемых гармониками. Звук самой низкой частоты называется первой гармоникой, которая определяет слышимый нами тон. Более высокие гармоники — музыкальные звуки, придающие ноте ее характерное качество, — имеют частоты, кратные частоте первой гармоники.

Стационарность представляет собой свойство волн в ограниченном пространстве. Такие волны легко вызвать в чашке чая. Де Бройль спрашивал — являются ли электроны атома локализованными (удерживаемыми) волнами? Если да, то образуют ли они дискретные стационарные волновые паттерны? Например, может быть, самая низкая атомная орбита — это та, на которой один электрон образует стационарную волну наименьшей частоты — первую гармонику, — а более высокие орбиты соответствуют стационарным электронным волнам более высоких гармоник (рис. 6).

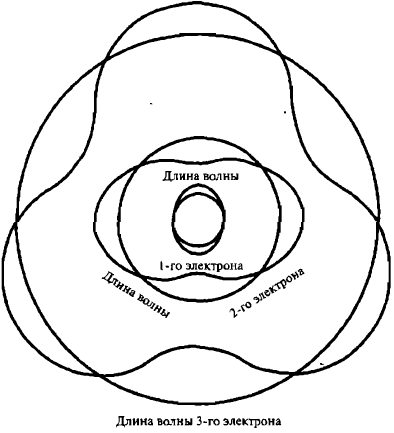
Рис. 6. Идея де Бройля: не могут ли электроны быть стационарными волнами в ограниченном пространстве атома?

Разумеется, де Бройль приводил в поддержку своей идеи гораздо более сложные доводы, но все равно ему было трудно добиться одобрения своей диссертации. В конце концов ее послали на отзыв Эйнштейну. Эйнштейну, который первым осознал двойственную природу света, было не трудно понять, что де Бройль вполне мог быть прав: материя вполне может быть такой же двойственной, как свет. Де Бройлю присудили искомую степень, когда Эйнштейн дал о его диссертации такой отзыв: «Это может выглядеть безумным, но, в действительности, это логично».

В науке окончательным арбитром всегда служит эксперимент. Правильность идеи де Бройля о волновой природе электрона блестяще продемонстрировал эксперимент, в котором пучок электронов пропускали через кристалл (трехмерный «зонтик», подходящий для дифракции электронов) и фотографировали. Получилась дифракционная картина (рис. 7).

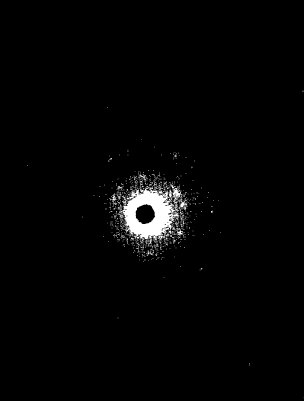
Рис. 7. Концентрические дифракционные кольца показывают волновую природу электронов

Если материя — волна, язвительно заметил один физик другому в конце проходившего в 1926 г. семинара, посвященного волнам де Бройля, то должно быть волновое уравнение, описывающее волну материи. Физик, которому принадлежало это замечание, сразу же забыл о нем, но тот, кто его услышал, — Эрвин Шрёдингер — в дальнейшем открыл волновое уравнение для материи, теперь известное как уравнение Шредингера. Оно является краеугольным камнем, заменившим в новой физике законы Ньютона. Уравнение Шрёдингера используется для предсказания всех удивительных качеств субмикроскопических объектов, обнаруживаемых в наших лабораторных экспериментах. Вернер Гейзенберг открыл это же самое уравнение еще раньше, но в менее четкой математической форме. Математический формализм, выросший из работ Шрёдингера и Гейзенберга, называется квантовой механикой.

Предложенная де Бройлем и Шрёдингером идея волны материи порождает удивительную картину атома. Она объясняет простыми терминами три самых важных свойства атомов: их устойчивость, их тождественность друг другу и их способность восстанавливаться. Я уже объяснял, как возникает устойчивость, — это был великий вклад Бора. Тождественность атомов определенного вида — это просто следствие тождественности волновых паттернов в ограниченном пространстве; структура стационарных паттернов определяется тем, каким образом ограничивается движение электронов, а не их окружением. Музыка атома, его волновой паттерн, остается одной и той же, независимо от того, где он находится — на Земле или в туманности Андромеды. Более того, стационарный паттерн, зависящий только от условий своего ограничения, не имеет никаких следов прошлой истории, никакой памяти; он снова и снова восстанавливается в том же самом виде.

Date: 2015-05-18; view: 1654; Нарушение авторских прав