
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Энергия связи ядер
|
|
Масса ядра не является аддитивной величиной: причиной является сильное взаимодействие нуклонов в ядре. Из-за этого взаимодействия для полного разделения ядра на отдельные свободные нуклоны необходимо произвести минимальную работу, которая и определяет энергию связи ядра ΔЕсв. Наоборот, при образовании ядра из свободных нуклонов эта энергия выделяется (в виде, например, электромагнитного излучения).
Известно, что энергия покоя частицы связана с ее массой соотношением Эйнштейна:
| E0 = mc2, | (2.2) |
Значит энергия покоя ядра всегда меньше суммы энергий покоя свободных нуклонов, входящих в состав ядра:
| ΔEсв = ∑mN − mяд, | (2.3) |
| ∑mN – сумма масс нуклонов, mяд – масса ядра. |
Более детально (2.3) записывается следующим образом:
| ΔEсв = [ Zmp + (A − Z)mn − M(A,Z) ] c2, | (2.4) |
Соотношение (2.4) называется энергией связи ядра относительно всех составляющих его нуклонов. Энергия связи представляет собой величину энергии, которую нужно затратить, чтобы разделить данное ядро на все составляющие его нуклоны. Очевидно, что энергию связи является мерой прочности (устойчивости) ядра.
Масса Δm, соответствующая энергии связи:
| Δm = Eсв / c2 = Zmp + (A − Z)mn − M(A,Z), | (2.5) |
называется дефектом массы ядра. На эту величину уменьшается масса всех нуклонов при образовании из них ядра.
Процесс полного расщепления ядра на составляющие его нуклоны является скорее гипотетическим. В действительности при делении ядер и других ядерных реакциях происходит распад ядра на два, реже более осколков. Знание энергии связи ядер позволяет рассчитать энергетический баланс не только для довольно редкого процесса полного расщепления, но и для любых процессов распада и взаимных превращений ядер. Например, энергия Ep отделения протона, т.е. минимальная энергия, необходимая для выбивания протона из ядра Z X A равна разности энергий связи ядер Z X A и Z-1X A-1:

| Ep = ΔEсв(Z,A) − ΔEсв(Z − 1,A − 1). |
Аналогично En энергия отделения нейтрона:

| En = ΔEсв(Z,A) − ΔEсв(Z,A − 1). |
Для выбивания из ядра α-частицы нужна энергия, равная:

| Eα = ΔEсв(Z,A) − ΔEсв(Z − 2,A − 4). |
Легко увидеть, что энергия связи может быть выражена через массы нейтральных атомов. Это вытекает из того, что масса атома отличается от массы ядра на Z электронных масс (с точностью до энергии связи электронов):

| ΔEсв = [ Z Mат(1H 1) + (A − Z)mn − Mат(A,Z) ] c2. | (2.6) |
Этот вариант формулы более удобен, так как в большинстве экспериментов измеряется масса атома, а не масса ядра. Поэтому в таблицах обычно приводятся значения масс нейтральных атомов.
Энергия связи любого ядра положительна; она должна составлять заметную часть его энергии покоя. Точные значения масс атомных ядер определяются с помощью специальных приборов, называемых масс-спектрометрами.
Энергия связи, отнесенная к массовому числу А называется удельной энергией связи нуклонов в ядре:

| Eуд = ΔEсв / A = Δmc2 / A. | (2.7) |
Величина Eуд показывает, какую энергию в среднем необходимо затратить, чтобы удалить из ядра один нуклон, не сообщая ему кинетической энергии. Величина Eуд уд имеет своё значение для каждого ядра. Чем больше Eуд, тем более устойчиво ядро. На рисунке 2.2 приведена зависимость Eуд от массового числа A.
Видно, что Eуд вырастает от 0 МэВ при А = 1 (протон) до 8.7 МэВ при A =50–60 (24Cr – 30Zn) и постепенно уменьшается до 7.5 МэВ для последнего встречающего в природе элемента (92U). Для сравнения, энергия связи валентных электронов в атоме порядка 10 эВ, что в миллион раз меньше. Из рисунка 2.2 видно, что наибольшей удельной энергией связи обладают ядра с массовыми числами в диапазоне от 50 до 60. С уменьшением или возрастанием A удельная энергия связи уменьшается с разной интенсивностью, так как уменьшение удельной энергии происходит по разным механизмам.
Главные причины различия в энергии связи разных ядер заключается в следующем. Все нуклоны, из которых состоит ядро, можно условно разделить на две группы: поверхностные и внутренние.
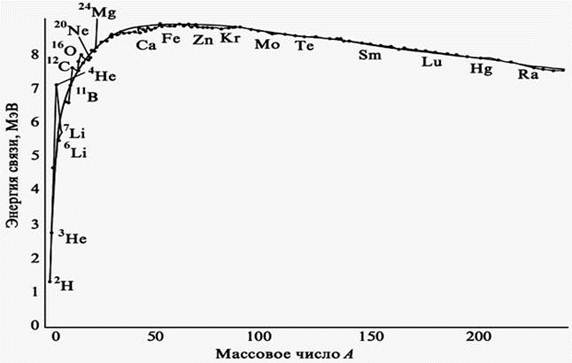
Рисунок 2.2. Зависимость удельной энергии связи E уд от массового числа A.
Внутренние нуклоны окружены соседними нуклонами со всех сторон, поверхностные же имеют соседей только с внутренней стороны. Поэтому внутренние нуклоны взаимодействуют с остальными нуклонами сильнее, чем поверхностные. Но процент внутренних нуклонов особенно мал у легких ядер (у самых легких ядер все нуклоны можно считать поверхностными) и постепенно повышается по мере утяжеления. Поэтому и энергия связи растет вместе с ростом числа нуклонов в ядре. Однако этот рост не может продолжаться очень долго, так как начиная с некоторого достаточно большого число нуклонов (A = 50–60) количество протонов становится настолько большим (практически в любом ядре протоны составляют не менее 40% общего числа нуклонов), что делается заметным их взаимное электрическое отталкивание даже на фоне сильного ядерного притяжения. Это отталкивание и приводит к уменьшению энергии связи у тяжелых ядер.
Различие в энергии связи разных ядер может быть использовано для освобождения внутриядерной энергии. Энергетически выгодно:
- деление тяжелых ядер на более легкие;
- слияние легких ядер друг с другом в более тяжелые.
Как в первом, так и во втором случаях получаются более прочные (более устойчивые) ядра, чем исходные. При обоих процессах выделяется огромное количество энергии; эти процессы в настоящее время реализованы практически: реакции деления ядер и реакции термоядерного синтеза ядер (глава 4).
Проблема термоядерного синтеза решена наполовину: освоен взрывной синтез.
Среднее значение <E уд > равно 8 МэВ, причем для большинства ядер E уд ≈ <E уд > = 8 МэВ. Поэтому энергия связи атомных ядер в первом приближении может быть выражена через массовое число соотношением:

| ΔEсв ≈ <Eуд>∙A ≈ 8 МэВ. | (2.8) |
Это соотношение позволяет сделать два вывода относительно свойств ядерных сил, связывающих нуклоны в ядре.
Из пропорциональности Δ Есв и A следует свойство насыщения ядерных сил, т.е. способность нуклона к взаимодействию не со всеми окружающими его нуклонами, а только с ограниченным их числом. Действительно, если бы каждый нуклон ядра взаимодействовал со всеми остальными (A – 1) нуклонами, то суммарная энергия связи была бы пропорциональна A ∙(A – 1) ≈ A2,не A.
Энергия связи является мерой прочности ядра. Особенно велика энергия связи у 2He4, 6С12, 8О16 и других четно-четных ядер.
Ядра с полностью заполненными оболочками являются наиболее устойчивыми – магические ядра, у которых число протонов Z или нейтронов N равно одному из магических чисел: 2, 8, 20, 28, 50, 82, 26.
Date: 2015-05-18; view: 1222; Нарушение авторских прав