Закон Ламберта

Величины, характеризующие излучение при квантовом и волновом рассмотрении.

Е=hλ; ;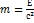

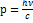
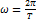;:T – период;

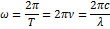
λ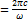

E=hν=eU

E=4,3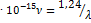

2. Фотометрические свойства тел. Типы отражения и пропускания. Ламбертовские источники и поверхности.

Закон Ламберта

Если яркость поверхностного источника излучения одинакова во всех направлениях, то для такого источника выполняется закон Ламберта, согласно которому сила излучения такого источника определяется по формуле:

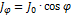
𝐽₀ – сила излучения в нормальном направлении;

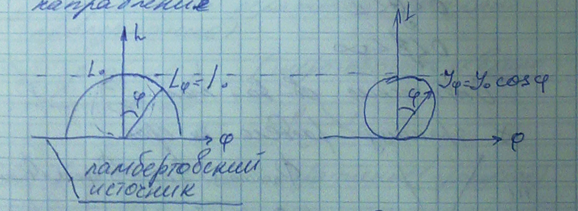
Ватман, MgO, BaSO₄, снег

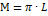
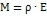
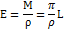
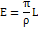
Виды отражения и пропускания:

Зеркальное отражение

Зеркальное отражение света отличает определённая связь положений падающего и отражённого лучей: 1) отражённый луч лежит в плоскости, проходящей через падающий луч и нормаль к отражающей поверхности, восстановленную в точке падения; 2) угол отражения равен углу падения j. Интенсивность отражённого света (характеризуемая коэффициентом отражения) зависит от j и поляризации падающего пучка лучей (см. Поляризация света), а также от соотношения показателей преломления n₂ и n₁ 2-й и 1-й сред. Количественно эту зависимость (для отражающей среды — диэлектрика) выражают формулы Френеля. Из них, в частности, следует, что при падении света по нормали к поверхности коэффициент отражения не зависит от поляризации падающего пучка и равен

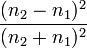
В важном частном случае нормального падения из воздуха или стекла на границу их раздела (показатель преломления воздуха = 1,0; стекла = 1,5) он составляет 4 %.

[править]Полное внутреннее отражение

Основная статья: Внутреннее отражение

Наблюдается для электромагнитных или звуковых волн на границе раздела двух сред, когда волна падает из среды с меньшей скоростью распространения (в случаесветовых лучей это соответствует бо́льшему показателю преломления).

С увеличением угла падения i, угол преломления также возрастает, при этом интенсивность отражённого луча растет, а преломленного — падает (их сумма равна интенсивности падающего луча). При некотором критическом значении i = i_k интенсивность преломленного луча становится равной нулю и происходит полное отражение света. Значение критического угла падения можно найти, положив в законе преломления угол преломления равным 90°:

sin i_k = n ₂ / n ₁

[править]Диффузное отражение света

При отражении света от неровной поверхности отраженные лучи расходятся в разные стороны. По этой причине нельзя увидеть свое отражение, глядя на шероховатую (матовую) поверхность. Диффузным отражение становится при неровностях поверхности порядка длины волны и более. Таким образом, одна и та же поверхность может быть матовой, диффузно-отражающей для видимого или ультрафиолетового излучения, но гладкой и зеркально-отражающей для инфракрасного излучения.

3. Идеальный рассеиватель. Коэффициент яркости.

Отражение (рассеяние) и излучение реальных источников обнаружения более или менее значительно отступает от закона Ламберта.

Яркость поверхности обусловлена освещенностью внешнего источника, и она зависит от величины, создающей ее освещение. Чтобы избежать неопределенности, вводится коэффициент яркости

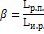
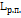– яркость реальной поверхности

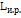– яркость идеального рассеивателя

Идеальный рассеиватель – материал,имеющий коэффициент отражения ρ=1,0 и который подчиняется закону Ламберта.

β_λ – спектральный коэффициент яркости

0<ρ<1,0

0<β<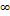

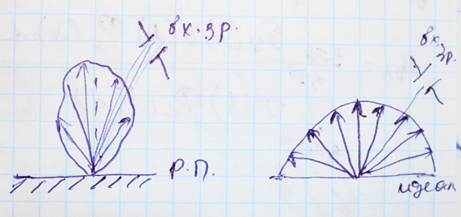
4. Яркость световой трубки. Изменение яркости при преломлении.

,

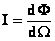где 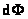- поток энергии излучения в телесном угле .

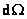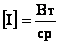
Поток излучения, испускаемый светящейся площадкой 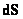в телесном угле 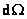, (рис.1.7.1) определяется как

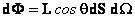, (1.7.10)

где 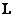- энергетическая яркость площадки, 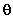- угол между нормалью к площадке и направлением хода лучей.

Для люминесцирующих и рассеивающих тел соотношение (1.7.10) несколько нарушается, так как надо учитывать зависимость яркости от углов 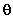и 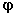в сферической системе координат (индикатрису излучения).

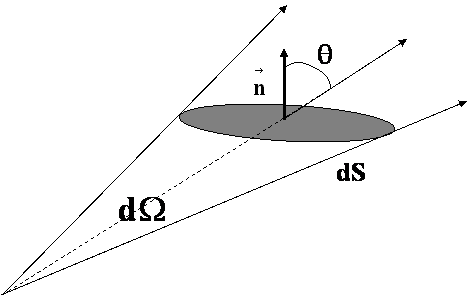
Рис.1.7.1. Пояснение к формуле (1.7.10)

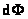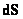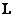Формула (1.7.10) работает, когда под яркостью понимают интенсивность светового потока (световой трубки), однако в данном варианте - поток энергии излучения от внешнего источника, проходящий через сечение световой трубки , а - яркость потока.

Из формул (1.7.9) и (1.7.10) следует, что

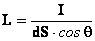, (1.7.11)

то есть яркость равна силе излучения, испускаемого в нормальном направлении с единичной площадки.

Все рассмотренные выше величины приводились в энергетических единицах и требовали объективных приёмников энергии. Однако, в более простом варианте в фотометрии используют своеобразную световую систему единиц, основанную на усреднённой чувствительности глаза человека. В данном случае при расчётах вводят функцию видност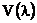и или 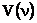, которая учитывает чувствительность глаза к свету разных длин волн или частот.

В этом случае основополагающей единицей стала единица силы света. 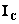- свеча (она составляет силы света, испускаемого с площади 1 смP^2P стандартного эталона по нормали к поверхности). Все фотометрические световые величины выражаются через свечу:

световой поток - люмен (Вт),

световая энергия 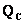- люмен·с (Дж),

сила света 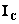- свеча=кандела (Вт·срP^-1P),

освещённость 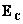- люкс=люмен·мP^-2P (Вт·мP^-2P),

светимость 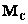- люкс (Вт·мP^-2P),

световая яркость 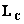- свеча·мP^-2P (Вт·мP^-2P·срP^-1P).

5. Интегрирующая сфера.

Это устройство незаменимо для измерения интенсивности излу-

чения от источников с произвольной индикатрисой. В спектроскопии

чаще всего оно используется для измерения коэффициентов отражения

диффузно отражающих образцов.

"Интегрирующая сфера" – распространенное название светомер-

ного шара Ульбрихта, одного из гениальнейших изобретений, вроде

колеса. Он позволяет простым методом решить сложнейшую задачу

сбора излучения во всем телесном угле 4π.

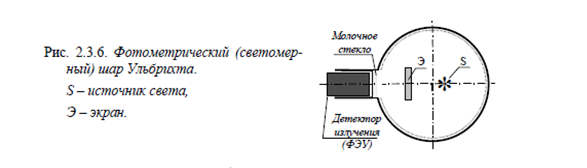
Классическая схема фотометра Ульбрихта показана на рис. 2.3.6,

из которого ясен и принцип действия.

На внутренней поверхности сферической полости радиуса R нане-

сено диффузно отражающее покрытие с коэффициентом отражения ρ,

близким к единице. Каждая точка поверхности шара освещена первич-

ным потоком от источника света S и вторичным, многократно переот-

раженным. Расчет показывает, что вторичная освещенность Е

одинакова для всех точек сферы, не зависит от места расположения ис-

точника и его диаграммы направленности, линейно зависит от светово-

го потока F, излучаемого источником и равна:

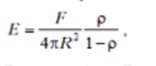
Если ρ → 1, то Е → ∞. Рожденный источником свет никуда не ис-

чезает, так что бесконечно накапливается. Поскольку всегда ρ < 1 и су-

ществуют потери света на неизбежных технологических отверстиях, в

том числе – для ввода излучения или самого источника излучения (как

на рис. 2.3.7), для вывода света на регистрацию и т.д., то Е всегда ко-

нечна. Более того, из-за потерь света возникает и неравномерность ос-

вещения внутренней поверхности. Идеальная равномерность может

быть достигнута при бесконечном числе переотражений, а в реальных

конструкциях оно составляет 10 – 100.

В стенке шара имеется небольшое отверстие, на которое не падает

первичный поток, а только – вторичный (для этого введен экран Э, по-

крытый таким же отражающим слоем, как и сфера). Освещенность окна определяется выражением (2.3.2). Но этот свет идет в окно из телесного угла 2π и его угловое распределение зависит и от положения источника.

Если детектор поместить непосредственно в окно, могут возникнуть

ошибки из-за анизотропии его чувствительности. Кроме того, само на-

личие окна нарушает условия, для которых получено соотношение

(2.3.2). Чтобы уменьшить эти неточности, окно закрывают светорассеи-

вающим экраном, например – молочным стеклом, желательно с матовой поверхностью. Оно большую часть излучения отражает и лишь малую пропускает. При этом угловые распределения падающего и прошедшего излучений не взаимосвязаны, так что показание фотоприемника будет пропорционально световому потоку, упавшему на окно. Однажды откалибровав такое устройство по известному источнику, можно проводить измерения абсолютных интенсивностей излучения любых других.

Для измерения коэффициента отражения незеркальных поверх-

ностей (в частности, прессованных порошков) такой шар используется

в несколько измененном виде. Поскольку положение источника S не

принципиально, то его можно поместить и на поверхности сферы, при-

чем – практически в любом месте. Обычно изображенный разрез расположен в приборе вертикально, а выходное окно и стоящий за ним ФЭУ расположены горизонтально. Здесь также нужны молочное стекло и экран для его защиты от первично отраженного образцом излучения (не показан).

В стенке сферы делают два отверстия, к которым снаружи прижимают образцы. Один – эталонный, второй – исследуемый, см. рис..3.7. Напротив них – также два отверстия для ввода излучения (по стрелкам) от модулирующего светоделителя 1 и для вывода зеркальной компоненты отражения. Часто интересуют только потоки, диффузно отраженные образцами, а зеркальная компонента может оказаться существенно интенсивнее диффузной.

Если же зеркальная компонента тоже нужна, то достаточно изменить геометрию так, чтобы она не попадала в световое отверстие. Например, можно при той 2 же расстановке образцов обойтись одним отверстием для ввода излучения, на рисунке – в нижней точке сферы. На выходе получается промодулированный сигнал. Дальше можно просто измерить амплитуду модуляции и получить абсолютную ве личину разности коэффициентов отражения. А можно независимо

измерить сигналы обеих фаз и вычислить отношение или разность ко-

эффициентов отражения. Каждый поступает, как ему надо. Но принци-

пиально важно, что оба отраженных потока регистрируются одним

детектором (ФЭУ). Это существенно повышает точность измерений,

т.к. сделать два детектора с одинаковой чувствительностью практиче- ски невозможно.

-

Выражение (2.3.2) справедливо для сферы без отверстий и для ко-

эффициента отражения, близкого к единице. Без отверстий обойтись

невозможно, но коэффициент отражения удается сделать довольно

близким к единице, см. рис. 2.3.8.

Подобные устройства часто используются для исследования цен-

тров окраски щелочногалоидных кристаллов или изменений спектров

поверхностей прозрачных порошков при различных обработках. Иными словами – слабых линий поглощения, возникающих в прозрачных веществах. Здесь важны именно диффузные компоненты отражения, так как они формируются в результате многократных переотражений на границах зерен порошка.

6. Поглощение света. Показатель поглощения и его физический смысл. Типы сред.

Прохождение излучения через прозрачную, но поглощающую среду приводит к его ослаблению, которое обусловлено поглощением его этой средой.

Количественно поглощение в простейших случаях описывается коэффициентом поглощения. Так, согласно закону Бугера — Ламберта — Бера интенсивность света, распространяющегося в поглощающей среде, спадает с расстоянием по закону:

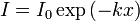
где I, I0 — интенсивности излучения в данной точке и в точке x = 0; k — коэффициент поглощения; x — координата вдоль направления распространения.

7. Оптическая плотность. Десятичный показатель поглощения и его измерение.

Оптическая плотность — мера поглощения света прозрачными объектами (такими, как фотоплёнка) или отражения света непрозрачными объектами (такими, как фотография).

8. Отражение от гладких поверхностей. Формулы Френеля. Угол Брюстера.

Формулы Френеля

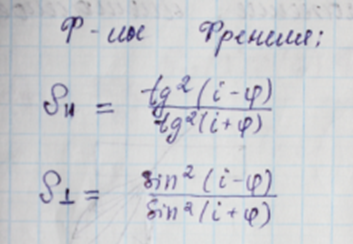
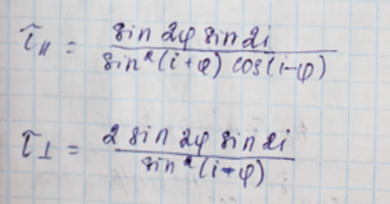
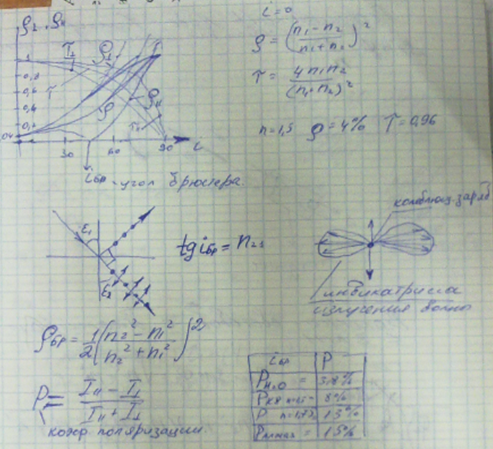
9. Отражение от менее плотной среды. Энергетические и фазовые соотношения. Эллиптическая поляризация.

Date: 2015-05-18; view: 6725; Нарушение авторских прав