Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Дәрістің тезистері
|
|
І модуль. Дәріс тақырыбы. Жарықтың толқындық қасиеті.
Дәріс жоспары:
1. Электромагнитті толқындар шкаласы
λ - нүктенің толық тербеліс кезіндегі жүріп өткен жолы.Бірдей фазада орын тербеліп тұрған екі нүктенің ара қашықтығы.Толық бір тербеліске кеткен уақыт (Т) период деп аталады. Дененің уақыт бірлігіндегі тербеліс саны оның жиілігі (ν) деп аталады.
ν=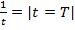 
= 
ν= 
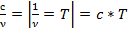
Ең қысқа ұзындықтағы электромагниттік толқын ол гамма сәулесі (ең үлкен жиілікте). Толқын ұзындығы қысқалау бірақ гаммадан үлкен рентген сәулесі. Неміс ғалымы Рентген анықтаған. Ультра күлгін сәуле шығару – жарық сәулелері спектрінің күлгін бөлігіне іргелес, күлгін және радиосәулелер аралығында орналасқан, толқын ұзындығы 400-10 нанометр (нм) аралығына сәйкес келетін электромагниттік сәулелер.Көрінетін сәулелер,радио толқындар.
λ = (3500:7500) А
1А =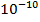 
м (Ангстром)= 0.1нм=0,1х 
м
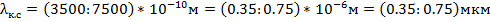
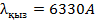
Жарықтың толқындық қасиеті.
XIX ғасырдың екінші жартысында Максвелл электромагнитті толқындардың тендеуін ұсынды. Біртекті (ε=const, μ=const) өткізбейтін (σ=0, ρ=0)біркелкі орта үшін Максвелл тендеулері келесідей жазылады.
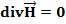
Мұндағы 
және 
электр және магнит өрістерінің кернеуліктері С жарықтың вакуумдағы жылдамдығы ε және μ ортаның электрлік және магниттік өтімділіктері.
2. Дәріс тақырыбы. Фотометрия
Дәріс жоспары:
1. Фотометрия заңдары.
Фотометрия деп – жарықты сипттауға арналған шамалар жиынын айтамыз.
Негізгі фотометриялық шамалар
Жарық ағыны деп берілген беттен уақыт бірлігінде өтетін жарық энергиясының мөлшерін айтамыз.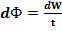 
; (𝟏)
Мұндағы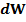 
, 
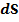бетінен t уақытта өтетін жарық энергиясының мөлшері (1) энергия келесі денелік бұрыш аралығында таралынуы
; (2)
Жарық күші деп бірлік денелік бұрышпен шығатын жарық ағынының шамасын айтаиыз.
I= 
; (3)
Изотропты жарық көздері үшін: I= 
; (4)
Мұндағы : Ф=4πI₀
Жарықтылық (яркость) деп жарық көзінің бірлік бетінен шығатын жарық күшін айтамыз.
Β= 
= 
; (5)
Жарқырау (светимость) деп бірлік беттен барлық бағытта тарайтын жарық ағынын айтамыз. S=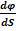 
; (6)
Жарықырау мен жарықтылық арасында келесідей байланыс бар. S=πΒ (7)
Жарықталыну деп жарық ағынының түскен бетке қатынасы бойынша анықталатын шаманы айтамыз. E=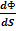 
; (8) немесе dФ=
Жарық шамаларының өлшем бірліктері.
Жарық шамаларының өлшем бірлгі. I~Kд (канделла)
Жарық ағыны dφ=I*dΩ=| I~Kд
Жарықталыну. E~1Лк (Люкс); 1Лк= 
Жарқырау. S~Лк
Жарықталық. B~Нт (нит)
3. Дәріс тақырыбы: Геометриялық оптика
Дәріс жоспары:
1. Геометрия оптика заңдары
Геометриялық оптика жарықтың таралуы сәулелермен өрнектеледі. Сәулелер бір-біріне тәуелсіз түзу сызық бабымен таралынады. Және орталар шекарасында сынады және шағылады.
Геометриялық оптиканың негізгі принципі – Ферма принципі;жарық бір нүктеден екінші таралған кезде экстремалды уақыт көтетін жолды таңдайды. Ферма принципі Гюгенс принципінің 
кезіндегі салдары болып табылады. Жарықтың сынуы ортаның сыну көрсеткішімен сыйпатталады.Оптикалық біртекті орта деп n=const ортаны айтамыз.Жарықтың түзусызық бойымен таралу заңы:оптиканың біртекті орта жарық сәулелері түзу сызық бойымен таралынады. Шағылу заңы түсу бұрышы шағылу бұрышына тең
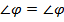1
Түскен сәуле,шағылған сәуле және түсу нүктесіне түрғызылған нормаль бір жазықтықта жатады.
Сыну заңы:түсу бұрышының синусының сыну бұрышының синусына қатынасы ортаның салыстырмалы сыну көрсеткішіне тең
1,2,.. мұндағы 
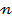1,2,.. 
Срда С большим n называется оптгесон более полной средой, а с меньшим – менее плычной, түскен сәуле,сынған сәуле, және түскен нүктесіне түрғызылған нормаль бір жазықтықтың бойында жатады.
Жарық оптиканың тығызырық ортадан екінші оптикалық тығыздығы аз ортасына өткен кезде сыну бұрышы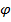 
2 = 
болуы мүмкін.яғни жарық екінші ортаға өтпейді. Бұл құбылыс толық ішкі шағылу деп аталады.
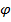Sin min= 
Линза деп екі сфералық бетпен шектесетін мөлдір денені айтамыз. Линза жұқа деп есептелінеді егер оның қалыңдығы сфералық беттің қыйсуының радиусымен салыстырғанда ескермеуге болатын болса, сфералық беттердің қыйысуының орталығы арқылы өтетін түзуді линзаның негізгі оптикалық осі деп атлады. Линзаның фокустық ара қашықтығы келесі өрнек бойынша анықталады.
= (n-1)(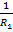
+ 
)
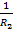Мұндағы n- линзаның сыну көрсеткіші, R1, R2- линзаның сфералық беттерініңқисықтық ререзиустері. Жинағыш линза үшін f 
, шашыратқыш линза үшін -f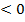 
.
Оптикалық жұиелердегі кескіннің айқын болмауы абберция деп аталады. Абберцияның болуы диаметірі үлкен, және көлбеулігі көп жарық ағынының қанаудан болды. Оның түрлері, сфералық абберация, хроматизалық абберция, дисторция, кома, астигматизм т.с.с.
4. Дәріс тақырыбы: Жарық интерференциясы
Дәріс жоспары:
1. Бірдей қалыңдықтағы және бірдей көлбеуліктегі интерференция
Интерференция дегеніміз – латынша «орала өту» дегенді білдіреді. Жарықтың интерференциясы деп – кеңістікте жарық толқындарының қосылған кезде бірін – бірі күшейту және әлсірету құбылтарын айтамыз. Бұл толқындар интерференция құбылыстарды береді егер олар когерентті болса.
Когерентті дегеніміз- өзара үлескен бір- біріне сәйкес толқындар
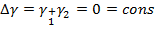
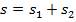
Жарық интерференциясы 2 –ге бөлінеді; қалындығы біркелкі интерференция, көлбеулігі біркелкі интерференциясы.
Қалыңдығы біркелкі интерференция – сына тәріздес ауа қабатында пайда болады. Бұған түскен жарық жартылай шағылады. Сынаның әрбір қалыңдығында өзінің малекулалары болады.
Пастинкамен жартылай линзаның арасында сына тәріздес ауа қабатында пайда болады. Мына осы аралықты концентірлі сақиналар түріндегі концентірлік жарық аламыз. Интерференциялық суреттер аламыз. Бұларды Ньютон сақиналары деп аталады. Өткен сақинадағы жарық сақинасының радиусы келесі түрде анықталады.
; (1)
Мұндағы: k-максималдардың реті, k=0,1,2,3……..
r- жартылай линзаның сфералық бетінің қисықтылық радиусы.
λ- қолданылатын жарықтың толқын ұзындығы;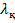 
= 6320 
; 
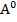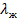= 5550 ;
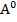Қараңғы жарықтың радиусы
; (2)
Шағылған жарық үшін бірінші өрнек қараңғы сақинаның радиусын береді ал екінші өрнек жарық сақинасының радиусын береді.
Ньютон сақинасын пайдалана отырып тәжірибеде әр түрлі денелердің сыну көрсеткіштерін немесе берілген ортада таралынатын жарықтың толқындық ұзындығын есепке аламыз.
Көлбеулігі біркелкі интерференция беттері өзара паралель жазық пластиналарда пайда болады.
Интерференциялық суреттер арақашықтығы бірдей интерференциялық жолақтар түрінде алынады. Бірдей бұрышқа түскен сәулелер өзінің интерференциялық суретін береді. Ал басқа бұрышқа түскен сәуле өзінің интерференциялық суретін береді.
Date: 2015-05-18; view: 1515; Нарушение авторских прав