Диффузия в газах

Предположим, что в единице объёма двухкомпонентной газовой смеси содержится n₁ молекул одного вида и n₂ молекул другого вида. Полное число молекул в единице объёма равно n = n₁ + n₂­. Допустим, что в направлении оси х создаются градиенты концентраций 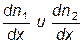, причём 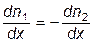. Тогда, , так что n, а, следовательно, и Р постоянны (в силу Р = nkT).

В этом случае газодинамических потоков не возникает. Однако вследствие теплового движения молекул будет происходить процесс выравнивания концентраций, сопровождающийся переносом массы каждой из компонент в направлении убывания её концентрации. Этот процесс носит название диффузии. Диффузия наблюдается так же в жидких и твёрдых телах.

Поток молекул i – го вида через перпендикулярную к оси х поверхность S определяется выражением

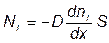,где D – коэффициент пропорциональности, называемый коэффициентом диффузии. Знак минус указывает на то, что поток молекул направлен в сторону убывания концентрации. Умножив обе части этого равенства на массу молекулы i – го вида m_i, получим выражение для потока массы i – ой компоненты:

,

где r_i = n_im_i – парциальная плотность i – ой компоненты.

Эти формулы представляют собой эмпирические уравнения диффузии. Их называют уравнением Фика.

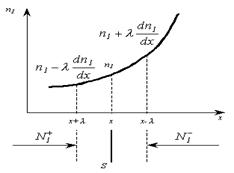
Получим уравнение диффузии, основываясь на молекулярно-кинетических представлениях, причём для упрощения расчётов будем считать, что молекулы обеих компонент мало отличаются друг от друга по массе (m₁» m₂» m) и имеют практически одинаковые эффективные диаметры (d₁» d₂» d). В этом случае молекулам обеих компонент можно приписывать одинаковую среднюю скорость теплового движения < u >, а среднюю длину свободного пробега вычислить по формуле 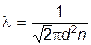, где n = n₁ + n₂.

Пусть изменение концентрации первой компоненты вдоль оси х даётся функцией n₁ = n₁ (x).

Поток молекул первой компоненты летящих через поверхность S в положительном направлении оси х, равен

,

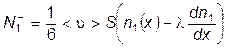а соответствующий поток молекул первой компоненты, летящих в отрицательном направлении оси х равен разности этих потоков

.

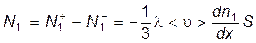Таким образом, мы пришли к уравнению диффузии Фика, причём получили для коэффициента диффузии выражение

.

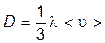Date: 2015-05-18; view: 600; Нарушение авторских прав