
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Бирюльки и фитюльки всемирного тяготения 7 page
|
|
То-то и климат на Земле, с её подачи, какой-то издерганный стал, то жары подпустит, то всё зальёт, то ураганчик подбросит, а то и снега навалит там, где его отродясь не видывали. Бедолаги метеорологи с ног сбились, пытаясь за прогнозом угнаться, хоть что-то уразуметь в погоде этой, ведь им же за планету отдуваться приходится. Но куда им за Землёй угнаться. Каши мало ели. И ведь не одна она на этой орбите крутится. Бедная Луна-спутница, устала к её выкрутасам приспосабливаться. И сама потихоньку, потихоньку от Земли отваливать нацелилась. Похоже от греха подальше. Хотя и Луна не пай девочка, тоже своими выкрутасами тешит, с ней ой как повозиться придётся. Но об этом потом.
А к тому же планета как-то странно приливами своими заправляет. Нет, чтоб, в согласии со старой доброй классической наукой по два приливных горба ежедневно по океанам таскать, так и норовит от одного избавиться. Тяжко ей, видите ли, с двумя управляться, несподручно как-то, да и нотации учёных надоело выслушивать. Всё поучают и поучают: «Горбатая ты двумя горбами». С одним-то горбиком попроще. Подумал я, подумал и порешил помочь Земле от одного горба избавиться. Пришлось внимательно присмотреться к её окружению и чтож оказалось? Соседи-то её по шубе (глобуле) так и норовят обжать её где-нибудь в укромном месте. А поскольку обжатие неравномерное, то и вращается бедняжка, асимметрично одним горбом наружу, как ей сподручнее. И что ещё интереснее, во вращение это ну никак не вмешивается её подружка – Луна. Устранилась она видите-ли. Кругами ходит, завидует, похоже, дуется, что на неё внимание не обращают. К тому же всё это горбатое вращение планеты на понятный язык, перевести можно, что я и попробую сделать.
Итак, начну.
Вещественная глобула Земли имеет свою плотность, которую определяет поверхностная плотность планеты. Глобула «плавает» в телесном пространстве Солнечной системы, и пространство это от точки к точке имеет изменяющуюся напряжённость гравитационного поля. Если это изменение, для примера, отнести к диаметру планеты, то окажется, что со стороны Солнца напряжённость составляет g1 = 0,593383 см/сек2, а с противоположной стороны g2 = 0,5928 см/сек2. Следовательно, если на солнечной стороне напряженность гравиполя Земли g3 = 981 см/сек2, то с противоположной стороны около g4 ≈ 980 см/сек2. Разница заметная, но она не фиксируется приборами, поскольку все тела, а вместе с ними и приборы деформируются пропорционально деформации Земли [27], и нужно знать, что искать, чтобы приборно обнаружить эту деформацию. Кстати её и обнаруживают, например, по поведению отвесов, но, не имея представления о деформации планеты, объяснить не могут.
Эта деформация приводит к тому, что радиус планеты Rс по экватору со стороны Солнца оказывается равен Rс = 6,378·108 см, с противоположной стороны он равен Rп = 6,381·108 см, что на 3 кмбольше. Т.е. при повороте планеты вокруг оси солнечная сторона сжимается, а противоположная расширяется, и планета как бы «коробится». А поскольку, похоже, коэффициент расширения воды больше, чем твердых пород (это ещё исследовать надо), то и волна от её расширения заметнее. И это волна расширения, а не лунного притяжения, и вода от неё не перетекает вслед за Луной, а просто под воздействием сжатия планеты и вместе с ней, сопротивляясь сжатию, вздымается и опускается, разжимаясь на выходе из действия внешней напряжённости, оставаясь практически на одном и том же месте. Вот почему не происходит перетекания воды в морях и океанах, которое обязано было происходить, поскольку Луна воздействовала бы на неё под углом к горизонту, т.е. «тянула» бы на себя воду. (То, что Луна никакого гравитационного влияния на Землю не оказывает, логически и без физических формул, вывел ещё 2001 г. не физик М.Ф. Аристархов [28].)
Другим следствием круговой деформации становится «перемещение» центра тяжести планеты, (правильнее ядра – центра напряжённости и испускания гравитационных волн) в солнечную сторону на 1,6 м, туда, где плотность пород повышается. Сжатие солнечной стороны Земли, не просто уплотняет её породы, но и изменяет период пульсации гравитационной волны, перемещая её центр в солнечную сторону. По этой же причине статический центр масс планеты «уплывает» от центра гравитационного притяжения, и, следовательно, центр тяготения и центр масс не совпадают друг с другом. Ещё одно подтверждение того, что массы умывают руки от гравитации. И отслеживая центр гравитационного притяжения, отвесы на поверхности уклоняются с периодом в солнечные сутки от центра масс планеты, а вместе с ними и вода морей и океанов Земли кругами следуют за перемещением гравитационного центра. Подробности этого круговращения очень хорошо показаны у О. Деревенского в тех же «Бирюльках…» поэтому я их касаться не буду.
И наконец, третьим следствием суточного коробления Земли стало ежедневное незначительное изменение положения звёзд на небе относительно местной опорной вертикали (их «гуляние» по-Деревенскому). Это «гуляние», разное для различных областей планеты, не имеет объяснения со второй половины ХIХ века и вообще, похоже, замалчивается. Одна из причин – не может же жёсткая Земля испытывать такую уйму короблений. Она ж не резиновая. Но это точка зрения ошибочна. Эти «коробления» не механические, а полевые. Механические колебания воздействуют на отдельные области тела, местами деформируя или разрушая их, а полевые воздействия охватывают объёмной деформацией всё тело, исключая механическую деформацию.
Таким образом, Луна, не имея гравитационного воздействия на Землю, не оказывает никакого влияния на формирование приливных горбов в морях и океанах. Это чисто планетарное явление, следствие взаимодействия пульсирующей Земли с пульсирующим эфирным пространством. И в то же время она отодвигается от поверхности планеты, и как доносят лазерные дальномеры, где-то на 17-20 см, ежегодно (естественно, дальномеры, глазами физиков, лукавят, отодвигается спутник на порядок-два дальше, но для начала поверим им). Хоть и маленькое, и вроде бы ничем человечеству не грозящее отодвигание, но его ведь тоже объяснить нужно, поскольку это явное и злостное нарушение законов классической механики. Это удаление на четверть (4-5 см) объяснялось до сих пор торможением, следствием образования приливных волн, остальные три четверти – не объяснялись ничем. Если же Луна никакого отношения к приливным волнам не имеет, то какие причины вынуждают Луну отдаляться от планеты, хотя бы 10 см.? Отложим ответ на этот вопрос и вернёмся к пульсациям планеты.
Поскольку все тела, включая звезды, планеты, спутники элементарные частицы и т.д., обладают самодвижением – пульсацией, и у звезд она наблюдается, то возникает вопрос, а можно ли на пульсирующей Земле эмпирически наблюдать за её пульсацией? Закон «всемирного» тяготения запрещает возможность такого наблюдения, поскольку все составляющие его параметры либо по постулату, либо по определению неизменны. Но на него, «всемирного», уже можно не реагировать, озаботившись только одним вопросом: Какие параметры можно выбрать для наблюдения, и каким способом вести наблюдение? В отделе Н.С. Лидоренко серьёзных приборов для гравитационных наблюдений не было, если не считать таковыми пару аптечных весов и одни лабораторные ВЛ-500.
Известно что, в процессе движения Земли по эллиптической орбите постоянно и зримо меняются два параметра – скорость на орбите и расстояние до светила. То возрастая, то, убывая, они как бы демонстрируют годовой период пульсации планеты. Возрастание и убывание этих внешних параметров должно было сопровождаться аналогичным изменением численной величины радиуса планеты и её массы, поскольку, как уже отмечалось, изменение любого внешнего или внутреннего параметра системы «тело», сопровождается изменением численной величины всех остальных. Изменение радиуса и массы планеты должно было сопровождаться инвариантным изменением веса тел и их объёма на поверхности. Эти изменения и было предложено использовать для отслеживания годовой пульсации Земли. Возможность же выявления изменения веса тел во времени, запрещённого парадигмой, при простоте проведения эксперимента, являлась достаточно веским основанием для эмпирической проверки указанных предположений.
Эти предположения подвигли к тому, что в середине 2005 года в НПО «Квант-Элемет» с одобрения Н.С. Лидоренко был начат эксперимент по длительному ежедневному (кроме выходных дней) наблюдению за изменением веса четырех твердых тел из ненамагничивающихся материалов. Были взяты: дубовый брусок, брусок из полимера, брусок дюралевый и свинцовый цилиндр. Для наблюдения за изменением веса использовались лабораторные весы ВЛ-500, обеспечивающие точность взвешивания в пять знаков (два знака после запятой). Естественно, что до проведения эксперимента отсутствовало представление о том, будет ли изменяться вес тел, каков характер изменения, его порядок, продолжительность, корреляция по отношению к возможному изменению гравиполя планеты и т.д. На начало эксперимента, образцы имели следующие параметры (таблица 2):
Таблица 2.
| № п⁄п | Материалы | Размер мм | Р, гр. |
| Дубовый брусок | 95х50х23 | 103,02 | |
| Брусок из полимера | 95х50х23 | 128,51 | |
| Брусок дюралевый | 74х48х21 | 195,79 | |
| Свинцовый цилиндр | 70; ø20 | 202,73 |
Достижение высокой точности измерения не предполагалось. Целью эксперимента было: в течение годового периода времени определить экспериментально на качественном уровне: изменяется ли вес указанных тел, тенденцию и примерный порядок этого изменения, если оно имеется.
Естественно, что эксперименты по изучению колебания веса тел во времени следует проводить в термостате и в вакуумной камере (увы, о такой роскоши и мечтать не приходилось. Это ж не РАН). Но не исключалась и возможность получения заметных результатов на лабораторных весах, поскольку прикидка влияния внешних воздействий (температуры, давления, влажности и т.д.) на изменение веса тел во времени показала, что их совокупное воздействие может вызывать изменение веса до пятого знака, т.е. как раз на пределе точности весов. К тому же используемые в эксперименте тела имели различные размеры, плотность, влагонасыщаемость и т.д., и потому указанные факторы должны были вызывать некоррелируемое изменение веса тел в процессе взвешивания за год.
Известно, что изменение веса, при взвешивании одного тела, оказывается строго пропорциональным изменению массы Земли, что, с высокой точностью (10-8-10-9), демонстрируют гравиметры. Поэтому и было взято несколько тел, чтобы исключить однозначную регистрацию взаимодействия.
Эксперимент проводился простым взвешиванием эталонных тел в течение года, и результаты оправдали ожидания. Оказалось, что вес всех тел изменяется во времени в различных пропорциях, а это свидетельствует о том, что получаемые численные изменения веса определяются свойствами тел. Количественные результаты измерения показаны в таблице 3:
| № | Размер | Макс. | Миним. | ||
| п/п | Материалы | мм | Р, гр. | Р, гр. | ∆ Р, гр. |
| Дубовый брусок | 95х50х23 | 104,89 | 98,26 | 6,63 | |
| Брусок из полимера | 95х50х23 | 128,79 | 127,78 | 1,01 | |
| Брусок дюралевый | 74х48х21 | 196,07 | 195,01 | 1,06 | |
| Свинцовый цилиндр | 70; ø20 | 203,1 | 202,07 | 1,03 |
Таблица 3
Вес всех тел (а, следовательно, и их массы) изменялся во времени в различных пропорциях, что с одной стороны свидетельствует об изменении напряженности гравиполя Земли, а с другой о том, что каждое тело имеет изменяемую по величине и во времени удельную гравитационную плотность.
Последовательное определение веса тел в одном месте в разное время года показывает, что вес их во времени меняется в четвертом, а иногда и в третьем знаке (при весе тела в пределах 200 гр.). И это изменение не находит в современной парадигме доказательного объяснения.
На графике 2 показаны ежедневные диаграммы изменения веса трёх тел за год, приведенные к 100 гр. весу (кроме дубового бруска). Вес дубового бруска меняется на несколько грамм, и это изменение коррелирует с временами года и с изменением веса других тел. Отсчет времени ведется с 01.07.05 г. по 01.07.06 г.
Здесь же, заодно, отмечу следующие факторы, сопровождавшие изменение веса:
• на графике 2 заметно, что вес всех тел на последний день проведения эксперимента оказался несколько больше чем в первый день наблюдения;
• колебания веса тел коррелировало между собой и происходило одновременно (и для дубового бруска) но количественная величина их была различной. Наблюдался ряд эффектов в изменениях веса тел:
• не мгновенная реакция тел на изменение внешнего гравиполя. Создается впечатление, что эта реакция, в какой-то мере связана с плотностью тел;
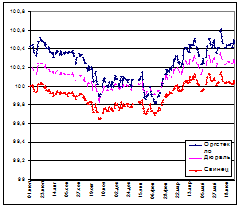 • в весенне-летние месяцы деревянный брусок реагирует на изменение напряженности гравиполя слабее, чем в осенне-зимний период;
• в весенне-летние месяцы деревянный брусок реагирует на изменение напряженности гравиполя слабее, чем в осенне-зимний период;
• брусок из оргстекла как бы слегка отображает «пове-дение» бруска из дуба;
• в зимний период отмечалось синхронное из-менение веса всех тел при значительных температурных перепадах (выделяются 20-30о морозы января – февраля 2006 г.).
График 2. Вывод: Земля пульсирует в гармонике нескольких периодов (в том числе с годовым периодом). Изменяющаяся в течение года вдоль орбиты напряженность гравиполя Солнечной системы деформирует параметры планеты, что отражается на весе тел, находящихся на ее поверхности.
Повторюсь: на графике2 отчетливо просматривается корреляция изменения веса тел за годовой промежуток времени, хотя количественные величины изменений не совпадают. Диаграммы изменения веса неорганических тел достаточно тесно коррелируют между собой, отображая неслучайный характер этого изменения во времени. А, следовательно, должны существовать некоторые внешние или внутренние факторы, обусловливающие данные изменения.
В астрономии используется система таблиц – эфемерид, предсказывающая на перспективу по дням скорости движения планет вокруг Солнца и их расстояния до него. Для определения ежедневной скорости планеты на орбите и расстояния от Земли до Солнца использовались таблицы эфемерид лаборатории реактивного движения (Калифорния, США) за 2005-2006 гг. Таблицы определяют основные прогнозируемые параметры орбитального движения планет на несколько лет.
Отмечу, — эфемериды рассчитываются исходя из парадигмы (из предположении) о том, что космическое пространство невещественно (пусто), изотропно от точки к точке, не имеет плотности и не оказывает никакого влияния на перемещающиеся в нём тела (планеты). Изотропность, в свою очередь, предполагает единую для всего пространства метричность. Само тело — планета, как система отсчета, в процессе инерциального движения по орбите не меняет своих размеров (не пульсирует), ее масса и радиус тоже не изменяются, а радиус орбиты изменяется достаточно монотонно.
Воспользуюсь эфемеридами и выясню, используя инвариантные уравнения из [29], коррелируют ли изменяющиеся параметры планеты, в ее орбитальном движении, с изменением веса тел на ее поверхности? Способы получения инвариантов кратко изложены в работах [2,18]. Ежедневная скорость v и величина радиуса орбиты R 1 планеты взяты из эфемерид. Усреднив эти величины по неделям, выбираю один из исследуемых предметов, например, свинец, и, приведя модуль средненедельной орбитальной скорости планеты к сопоставимой с модулем аналогичного изменения веса свинцового цилиндра, сравниваю на графике диаграммы их изменения за год (график 3).
На графике 3 видно, что изменение модулей скорости и веса происходит разнонаправленно, но, тем не менее, коррелирует друг с другом, только диаграмма веса несколько сдвинута влево относительно диаграммы скорости. Отмечу, что диаграмма скорости на графике 3 отображает волнообразное ежемесячное изменение скорости движения планеты, которое в принципе не допускает классическая механика, поскольку оно ставит под 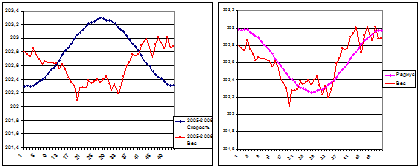
сомнение движение планеты по инерции.
График 3. График 4.
Проведу аналогичное построение графика еженедельного изменения веса свинца на поверхности планеты и радиуса её орбиты (график 4.). Диаграммы изменения веса свинца и радиуса орбиты однонаправленны и корреляция их изменения, так же, как и сдвиг влево диаграммы веса, проявляется более четко. Поскольку изменение скорости орбитального движения планеты и радиуса орбиты жестко связаны между собой инвариантом:
Rv2 – const,
то можно предположить, что скорость, на графике 3отображает наблюдаемую (фактическую) величину, а расстояние от планеты до светила (граф. 4.) – величину расчётную. А если допущен расчет радиуса орбиты без учета скорости движения планеты (как принято), то следует ожидать, что вследствие этой ошибки в афелии и перигелии не будут совпадать дни экстремальных значений скорости и радиуса, хотя средний радиус орбиты может остаться неизменным, а возрастут большая полуось и коэффициент эллиптичности, что и наблюдается в реальности [31].
График 4 свидетельствует – расчетное изменение радиуса орбиты (диаграмма «радиус») пропорционально изменению орбитальной скорости (график 3, диаграмма «скорость»). Диаграмма «вес» — изменения веса свинца с некоторым отставанием «копирует» изменение орбиты планеты, уменьшаясь к перигелию, где напряженность гравиполяСолнечной системынаибольшая и возрастая к афелию — где онанаименьшая. Таким образом, график отображает то обстоятельство, что изменение веса тел на поверхности Земли обусловлено прохождением планеты по областям изменяющейся напряженности гравиполя Солнечной системы. Выяснилось еще одно обстоятельство: диаграмма изменения веса как бы дрейфовала на графике, отображая место нахождения Земли на орбите (т.е. по изменению веса тел в течение года еще во времена И. Ньютона можно было приблизительно отслеживать орбитальное движение планеты, не заглядывая при этом на небо). А, следовательно, изменение напряженности гравиполя Земли напрямую связано с изменением гравиполя той области Солнечной системы, в которой находится планета.
Констатирую:
Изменения веса свинца во времени (как и оргстекла и дюралевого бруска) коррелирует с пропорциональным изменением орбитальной скорости и радиуса планеты.
С первого октября 2008 года ежедневное взвешивание четырех различных тел стали проводить в Челябинске (А. Королёв, А. Андреев) и в Перми (С. Гусаров).В Челябинске используются весы с четырьмя значащими цифрами, с одним знаком после запятой, и взвешиваются тела из оргстекла, дюраля, свинца и деревянный брусок. Тела подобраны случайным образом. Методика взвешивания – обычная. В Перми с 01.10.08 г. и по 01.10.10 г. завешивались также четыре тела: дерево, камень, железо, пластик. Параметры тел отображены в таблице 5, а динамика изменения веса на графике 6.
Таблица 4.(Челябинск)
| № | Тело | Нач. вес г. | max. Р г. | min. P г. | ∆Р г. |
| 1. | Оргстекло | 100,4 | 100,46 | 99,89 | 0,48 |
| 2. | Дюраль | 100,2 | 100,29 | 100,16 | 0,13 |
| 3. | Свинец | 100,0 | 100,06 | 99,94 | 0,12 |
| 4. | Дерево | 100,6 | 100,83 | 94,44 | 6,39 |
В таблицах 4-5 показана максимальная разница ∆Р в весе тел, приведенным к 100 г., за первый год наблюдения. Графики 5-6 демонстрируют динамику изменения одного из тел. И хотя в диаграммах изменения веса наличествует существенная разница (изменение веса ∆Р твердых тел с западной стороны Урала и с его восточной стороны отличаются значительно), некоторая корреляция динамики прослеживается. Наблюдаются достаточно значительные изменения, которые свидетельствуют о том, что амплитуда самопульсации Земли составляет сотни километров в год [32].

 График 5. График 6.
График 5. График 6.
Таблица 5. (Пермь)
| № | Тело | Нач. вес г. | max. Р г. | min. P г. | ∆Р г. |
| 1. | Камень | 100,7 | 100,78 | 100,19 | 0,59 |
| 2. | Железо | 100,4 | 100,47 | 99,82 | 0,65 |
| 3. | Пластик | 100,1 | 100,28 | 99,77 | 0,51 |
| 4. | Дерево | 101,0 | 102,53 | 100,70 | 1,83 |
В сентябре 2009 г. в Москве ученые МГУ (Рукин М., Жарвин Н., при участии автора [33-35]) решили экспериментально проверить изменение веса девяти тел при длительным взвешиванию. Эксперимент проводился в главном здании МГУ на 27 этаже. Для проведения эксперимента использовались электронные весы закрытого типа, KEPN 770/GS/Gc/, версии 2.3 04/2000 г., точность измерения (в граммах) – пятый знак после запятой. На графиках 7-14 (см. приложение 3) отображены завешиваемые тела и видно, что все они, (кроме дерева), в течение всего времени наблюдения сначала медленно уменьшают свой вес, а затем, ещё медленнее его наращивают.
Но вот какая ситуация: в последний день наблюдения, ни в Москве, ни в Челябинске, ни в Перми, ни одно тело не вернулось к своему первоначальному весу (похоже, даже не стремилось к этому возвращению). Более того, характер изменения веса всех тел в 2010 году резко отличается от того, что наблюдалось в предыдущем году и в 2005-06 гг. Создаётся впечатление, что в самопульсации Земли происходят какие-то изменения. Это, скорее всего, говорит о том, что происходит медленное и глобальное изменение положения Земли в пространстве. Об этом же свидетельствует и изменение климата в регионах планеты, и ежегодное возрастающее удлинение орбиты Луны, и начавшееся замедление скорости собственного вращения планеты и, зафиксированное в конце ХХ века, замедление скорости движения Нептуна и Плутона, и ряд других факторов. Земля по закручивающей спирали с ежегодным возрастающим ускорением приближается к Солнцу. И всё, что на ней происходит с климатом и катастрофами, будет в дальнейшем определяться этим процессом.
Добавлю: при исследовании изменения веса тел во времени в МГУ было обнаружено воздействие некоторых тел (слюда,опал) на тарелочку весов до того, как на нее было положено тело [34]. Эффект проявился в 4-м, 3-м и даже 2-м знаке после запятой и при внесении некоторых других тел во внутреннее пространство над чашечкой на высоте 0,5-2 см (без касания весовой площадки). Это было необычно и свидетельствовало о том, что к чашечке весов подносятся как бы наэлектризованные предметы, а чашечка заряжена одноименно с ними. Однако дальнейшие исследования показали, что эффект действительно вызывается наличием статического заряда на поверхности тел, подносимых к чашечке но не на самой чашечке. На чашечке одноименный заряд обнаружен не был, хотя эффект отталкивания доходил до 4-х граммов. К тому же на чашечку совершенно одинаково, но с разным числовым результатом воздействовали и положительно и отрицательно заряженные предметы, эффект полностью соответствовал гравитационному волновому отталкиванию.
Проводилось исследование и воздействия электризации на тела, находящиеся на чашечке весов. Эксперимент состоял в следующем: На чашечке весов поочередно завешивали и укладывали различные тела, а затем к ним подносили, без соприкосновения, наэлектризованную стеклянную палочку или полистироловую линейку на высоте 5-10 мм (табл. 6). Вес тел уменьшался, причем изменение веса наблюдается как у металлических, так и у стеклянных, пластиковых, деревянных и иных физических тел. Приведу, для примера, таблицу 6 изменения веса наэлектризованных тел:
Таблица 6
| Оргстекло | Дерево | Олово | Свинец | Парафин | Опал | Пемза | Дюраль | Цело- фан | |
| Начал. вес | 15,04059 | 5,09438 | 5,8921 | 10,0909 | 10,06627 | 0,9653 | 4,5351 | 7,7840 | 0,9605 |
| Стекл. пал. | 14,37 | 3,05 | 5,4 | 9,36 | 9,51 | 0,39 | 4,36 | 6,45 | 0,40 |
| Полис. лин. | 13,34 | 2,87 | 5,2 | 9,23 | 9,16 | 0,14 | 4,23 | 4,56 | 0,29 |
Проводились эксперименты и по воздействию на чашечку магнитов. Например, на столик весов были поставлены плашки, на которые, на высоте ~6 мм над чашечкой, положена дюралевая пластина, а на неё магнит сначала полюсом S, а затем N. При этом зафиксирован различный по величине виртуальный вес от воздействия обоих полюсов: S = 0,79072 г., N = 0,68238 г. Электроскоп наличия электростатического заряда на столике не показывал и на магнит не реагировал.
Положенная на дюралевую пластинку наэлектризованная пластмассовая линейка показывала виртуальный вес ~3,9 г. При снятии линейки и других предметов с подставки над чашечкой весов, чашечка показывала остаточный вес примерно от 0,012 г. до 0,00426 г. неэлектрического происхождения, который постепенно сходил на нуль.
К тому же, ежедневное завешивание на дюралевой пластинке магнита как северным, так и южным полюсом показала, что намагниченность каждого поля систематически меняется, изменения эти не всегда пропорциональны и гомогенны (график 7.).

График 7.
Эксперименты проделаны многократно с различными телами, повторяемость результатов – стопроцентная.
Строение Луны
А теперь вернусь к Луне. Чтобы охарактеризовать её «поведение» на орбите необходимо понять её происхождение, структуру и взаимодействие с пространством глобулы Земли. Однако в вопросе о происхождении Селены, как впрочем и остальных спутников и планет Солнечной системы, царит полная неопределённость. Существует множество гипотез, объясняющих отдельные эпизоды возможного происхождения некоторых тел Солнечной системы, но ни одна из них не образует её общей истории. Вот что говорится о Луне в одном из последних астрономических обзоров ([12] стр. 44.):
«В вопросе происхождения Луны пока нет полной ясности. Особенности химического состава лунных пород позволяют предположить, что Луна и Земля образовались в одной и той же области Солнечной системы. Однако разница в их составе и внутреннем строении заставляет думать, что оба эти тела не были в прошлом единым целым (и как всегда, следуя парадигме, – пальцем в небо – А.Ч.). В настоящее время одна из наиболее популярных теорий происхождения Луны – теория косого удара (ну не могут наши учёные в представлении космических явлений обходиться без бомбардировок, не могут, тут уж ничего не поделаешь – А.Ч.): предполагается, что в период формирования планет о Землю ударилось тело размером с Марс (не хилое, однако, и куда оно подевалось? В Солнечной системе такая глыба пропасть не может. Глобула не позволит. – А.Ч.), в результате чего значительная часть вещества коры и верхней мантии Земли была вырвана. Часть рассеянного при этом вещества сначала образовала кольцо обломков вокруг Земли, а затем слипание этих обломков привело к формированию нашего естественного спутника (слипание, при наличии глобул – невозможно – А.Ч.). На самой ранней стадии существования Луны, в период от 4,3 до 4,6 млрд. лет назад, произошла глобальная магматическая дифференциация (разделение) лунного шара, в результате которой сформировалась лунная кора и верхняя мантия. Этот процесс сопровождался интенсивной метеоритной бомбардировкой и падением фрагментов, оставшихся после основного этапа формирования Луны.
Большинство лунных кратеров и огромные впадины (многокольцевые бассейны) появились на поверхности лунного шара в период сильной бомбардировки поверхности (почему-то здесь не отмечается, что «бомбардировка» происходила со стороны Земли, космос оказался более миролюбивым, на поверхности с другой стороны Луны кратеров на порядок меньше. – А.Ч.). Около 3,5 млрд. лет назад в результате внутреннего разогрева (а может – наружного? – А.Ч.) из недр Луны излились на поверхность базальтовые лавы, заполнившие низины и круглые впадины. Так образовались лунные моря. На обратной стороне из-за более толстой коры излияний было значительно меньше. На видимом полушарии моря занимают 30% поверхности, а на обратном – лишь 3%. Таким образом, эволюция лунной поверхности в основном завершилась около 3 млрд. лет назад. Метеоритная обработка продолжалась, но уже с меньшей интенсивностью. Основную массу бомбардирующих тел в настоящее время составляют микрометеориты. В результате длительной переработки поверхности образовался верхний рыхлый слой пород Луны – реголит, толщиной в несколько метров.
Date: 2015-05-17; view: 537; Нарушение авторских прав