Интерференция света при отражении от тонких пленок. Полосы равной толщины и равного наклона. Кольца Ньютона

Для видимого света (например, солнечный свет). интерференционные полосы можно наблюдать для достаточно тонкой пластинки, толщиной d ~ 0.05 до 0.06 мм. Эта толщина обусловлена выполнением условий пространственной и временной когерентности. Когда лучи параллельны и падают под одним и тем же углом, то наблюдение интерференционных полос возможно на бесконечности. И наблюдают их с помощью линзы, либо глаза (который работает как линза), аккомодированного на бесконечность. Линза фокусирует параллельные лучи, идущие под одним углом, в одну определенную точку на фокальной плоскости (рис. 3.2).

Если падает монохроматический свет рассеянный, т.е. световые лучи падают под разными углами на тонкую плоскопараллельную пластинку, то линза собирает в точки те лучи, которые соответствуют равному наклону или углу падения. Параллельные лучи собираются в точку на фокальной плоскости (экране), как показано на рис. 3.3. Но если лучи падают со всех сторон, но под одним и тем же углом падения (т.е. для одного угла падения лучи распределяются по конусу над поверхностью пластинки), то на экране после собирающей линзы получаем освещенное кольцо. Получающиеся интерференционные полосы носят название полос равного наклона, т.к. они образованы светом, падающим пол одним углом падения к нормали. Если имеем белый свет, то полосы окрашены в разные цвета, поскольку для разных длин волн максимумы наблюдаются при различных углах падения. Так, человеческий глаз фиксирует различие в цвете при разности длин волн ∆λ~0.02 мкм = 20A.

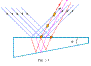Рассмотрим тонкую пластинку переменной толщины (угол φ между плоскостями – малая величина), на которую падает параллельный пучок света. Лучи отраженные от верхней

поверхности (на рис. 3.4 – синие) и нижней поверхности (красные) – не параллельны. Интерференционные полосы локализуются

на поверхности. При малых углах φ оптическую разность хода можно также вычислять по формуле для параллельных

пластинок (2.3.5), где d – толщина пластинки в данном месте.

Наблюдают эти полосы также с помощью линзы. На экране получаются полосы равной толщины, т.е. получаем интерференционные полосы, где разность хода одна и та же, или одна и та же толщина пластинки d. Интерференционные полосы наблюдают как в отраженном, так и в пройденном свете.

На практике глаз часто видит интерференционную картину при отражении солнечного света от тонких

пленок на воде или других материалах (мыльные, нефтяные, бензиновые пленки, цвета побежалости и т.д.).

Эти полосы обычно окрашены, поскольку условия для появления полос различны для разных длин волн.

Такой вид интерференции используется для определения качества ровной поверхности различных

материалов.

Кольца Ньютона.

Кольца Ньютона – один из ярких примеров полос равной толщины. Роль тонкой пластинки играет

воздушный зазор между линзой большого радиуса и подложкой. Интерференционная картина симметрична

относительно оси симметрии и имеет вид светлых и темных колец при освещении монохроматическим

светом. Интерференционные полосы можно наблюдать как в отраженном, так и в пройденном свете. В

отраженном свете интерферируют лучи, отраженные от подложки и от нижнего края линзы.

Рассмотрим условия интерференции в отраженном свете при условии, что линза помещена в воздухе

(см рис. 3.5). Поскольку радиус линзы достаточно велик, а интерференционная картина разворачивается

вблизи точки касания линзы и подложки, то вблизи точки касания (R >> r) можно пренебречь кривизной

линзы. Тогда оптическая разность хода определяется соотношением (в воздухе n = 1):

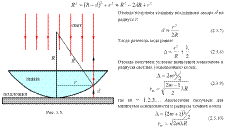
Интересно отметить, что в отраженном свете в центре (m = 0) мы имеем темное пятно.

Если рассматривать интерференционную картину в пройденном свете, то светлые и темные полосы

поменяются местами, – станут соответственно темными и светлыми. Линзу можно помещать в различные

среды и ставить на различные подложки, при этом необходимо учитывать показатели преломлений всех

сред при вычислении оптической разности хода.

Date: 2015-05-17; view: 2076; Нарушение авторских прав