Погрешности оптических приборов

Оптическая система. Тонкая линза представляет простейшую оптическую систему. Простые тонкие линзы применяются главным образом в виде стекол для очков. Кроме того, общеизвестно применение линзы в качестве увеличительного стекла (лупы).

Действие многих оптических приборов — проекцион­ного фонаря, фотоаппарата и др.— может быть схемати­чески уподоблено действию тонких линз, как об этом упо­миналось в § 97. Однако тонкая линза дает хорошее изобра­жение только в том сравнительно редком случае, когда можно ограничиться узким одноцветным пуч­ком, идущим от источника вдоль главной оптической оси или под небольшим углом к ней. В большинстве же практи­ческих задач, где эти условия не выполняются, изображение, даваемое тонкой линзой, довольно несовершенно. Поэтому в большинстве случаев прибегают к построению более сложных оптических систем, имеющих большое число пре­ломляющих поверхностей и не ограниченных требованием близости этих поверхностей (требованием, которому удов­летворяет тонкая линза).

§ 100. Главные плоскости и главные точки системы. Осу­ществим сложную оптическую систему, расположив не­сколько линз одну за другой так, чтобы их главные оптиче­ские оси совпадали (рис. 224). Эта общая главная ось всей системы проходит через центры всех поверхностей, ограни­чивающих отдельные линзы. Направим на систему пучок параллельных лучей, соблюдая, как и в § 88, условие, чтобы диаметр этого пучка был достаточно мал. Мы обна­ружим, что по выходе из системы пучок собирается в одной точке F' ', которую, так же как и в случае тонкой линзы, назовем задним фокусом системы. Направив параллельный пучок на систему с противоположной стороны, найдем передний фокус системы F. Однако при ответе на вопрос, ка­ково фокусное расстояние рассматриваемой си­стемы, мы встречаем затруднение, ибо неизвестно, до какого места системы надо отсчитывать это расстояние от точек F и F'. Точки, аналогичной оптическому центру тонкой лин­зы, в оптической системе, вообще говоря, нет, и нет основа­ний отдать предпочтение какой-нибудь из многих поверхно­стей, составляющих систему; в частности, расстояния от F

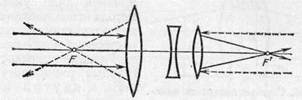
Рис. 224. Фокусы оптической системы

и F' до соответствующих наружных поверхностей системы не являются одинаковыми.

Эти затруднения разрешаются следующим образом.

В случае тонкой линзы все построения можно сделать, не рассматривая хода лучей в линзе и ограничившись изо­бражением линзы в виде главной плоскости (см. §97).

Исследование свойств сложных оптических систем пока­зывает, что и в этом случае мы можем не рассматривать дей­ствительного хода лучей в системе. Однако для замены слож­ной оптической системы приходится использовать не одну главную плоскость, а совокупность двух главных плоскостей, перпендикулярных к оптической оси системы и пересека­ющих ее в двух так называемых главных точках (H и H '). Отметив на оси положение главных фокусов, мы будем иметь полную характеристику оптической системы (рис. 225). При этом изображение очертаний наружных поверх­ностей, ограничивающих систему (в виде жирных дуг рис. 225), является излишним. Две главные плоскости сис­темы заменяют единую главную плоскость тонкой линзы: переход от системы к тонкой линзе означает сближение двух главных плоскостей до слияния, так что главные точ­ки H и H ' сближаются и совпадают с оптическим центром линзы.

Таким образом, главные плоскости системы представля­ют собою как бы расчленение главной плоскости тонкой лин­зы. Это обстоятельство находится в соответствии с их основным свойством: луч, входящий в систему, пересекает первую главную плоскость на той же высоте h, на какой выходящий из системы луч пересекает вторую главную плоскость (см, рис. 225).

Мы не будем приводить доказательства того, что такая пара плоскостей действительно существует во всякой опти­ческой системе, хотя доказательство это и не представляет

особых трудностей; огра­ничимся лишь указанием метода использования этих характеристик системы для построения изображения. Главные плоскости и главные точки могут ле­жать и внутри и вне системы, совершенно не­симметрично относительно поверхностей, ограничивающих систему, например даже по одну сторону от нее.

С помощью главных плоскостей решается и вопрос о фокусных расстояниях системы. Фокусны­ми расстояниями оптической системы называются рассто­яния от главных точек до соответствующих им фокусов. Таким образом, если мы обозначим F и Н — передний фокус и переднюю главную точку, F' и Н' — задний фокус и заднюю главную точку; то f'=H'F' есть заднее фокусное расстояние системы, f=HF — ее переднее фокусное расстояние.

Если по обе стороны системы находится одна и та же сре­да (например, воздух), так что в ней расположены передний и задний фокусы, то

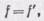(100.1)

как и для тонкой линзы.

§ 101. Построение изображений в системе. Зная положение главных и фокальных плоскостей системы, мы можем построить изображение в системе, совершенно не интере­суясь ее конкретными свойствами — числом преломляющих поверхностей, их положением и кривизной и т. д. Для построения достаточно провести какие-нибудь два луча из числа тех, построение которых может быть выполнено без затруднений. Ход этих лучей изображен на (рис. 226). Луч 1 падает на систему параллельно глав­ной оси; если этот луч пересекает переднюю главную плоскость в точке Q, то по свойству главных плоскостей

Рис. 225. Главные плоскости опти­ческой системы

он пересечет заднюю главную плоскость в точке Q ' на той же высоте над осью и пройдет, выйдя из системы через задний фокус F'.

Луч 2 проходит через передний фокус и пересекает главную плоскость в точке R; он пройдет на той же высоте (R'H'=RH) через заднюю главную пло­скость и выйдет из системы параллельно главной оси.

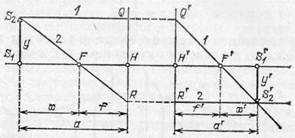
Рис. 226. Построение изображения в оптической системе

Указанная пара лучей может быть использована для по­строения изображения точки S ₂ в данной системе. В соответ­ствии с этим отрезок S ₁ S ₂ изобразится в виде отрезка S' ₁ S' ₂.

§ 102. Увеличение системы. Найдем теперь формулы для линейного увеличения b системы. Из подобия треугольников S' ₁ S' ₂ F' и H'Q'F' (рис. 226) имеем

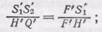
но S '₁ S '₂= y ', H'Q'=HQ=S ₁ S ₂ =y, F'H'=f.' Таким образом, обозначив через х' расстояние от заднего фокуса до изоб­ражения, находим

(102.1)

Тем же путем из подобия треугольников S ₁ S ₂ F и HRF нахо­дим

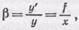(102.2)

где х — расстояние предмета от переднего фокуса. (Для рассматриваемых нами систем (см. § 100) f=f '.)

Наряду с линейным увеличением для характеристики действия оптической системы, как и в случае тонкой линзы (см. §96), большое значение имеет угловое увеличение.

Угловым увеличением g называется отношение тангенсов углов а' и а, составляемых лучами, выходящим из системы и падающим на систему, с оптической осью, т. е.

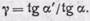(102.3)

С помощью рис. 227 можно показать (см. упражнение 45), что, так же как и в случае тонкой линзы,

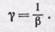(102.4)

Это означает, что чем больше размеры изоб­ражения, тем меньше ширина световых

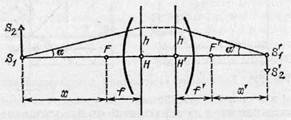
Рис. 227. Угловое увеличение оптической системы

пучков, образующих это изображение (ср. § 96). В § 109 этой главы будет показано, какое значение имеет это об­стоятельство для вопросов, связанных с освещенностью и яркостью изображений, даваемых оптическими системами.

§ 103. Недостатки оптических систем. Рассматривая об­разование изображений протяженных объектов в оптиче­ских системах, мы все время предполагали, что изображение образуется узкими световыми пучками и что они падают на систему под небольшими углами к ее главной оптической оси. И то и другое предположения практически в оптиче­ских приборах не выполняются. Для получения больших освещенностей приходится пользоваться широкими свето­выми пучками, т. е. применять линзы большого диаметра. Второе предположение также не выполняется во всех тех случаях, когда прибор должен дать изображение точек, зна­чительно удаленных от его главной оси, например при фотографировании. Отказываясь от этих ограничений, мы ухудшаем оптическое изображение: изображение оказы­вается, вообще говоря, не вполне резким, расплывчатым; мелкие детали смазываются и становятся неразличимы.

Кроме того, иногда теряется точное подобие между предме­том и его изображением.

Необходимо считаться еще с одним явлением, влияющим на качество изображения в оптической системе, именно, с зависимостью показателя преломления оптических стекол от длины волны. Эта зависимость приводит к тому, что края изображения, полученного с помощью белого света, оказываются окрашенными.

Полное устранение всех вышеперечисленных недостат­ков оптического изображения в реальных системах невоз­можно. Однако тщательное изучение погрешностей оптиче­ских систем позволяет найти пути для уменьшения их влияния, и в современных оптических приборах эти по­грешности настолько уменьшены, что незначительно ска­зываются на качестве изображения.

Погрешности оптических систем называют аберрациями. Ниже мы рассмотрим главнейшие аберрации и способы их устранения.

§ 104. Сферическая аберрация. Возникновение этой по­грешности можно проследить с помощью легко доступных опытов. Возьмем простую собирающую линзу 1 (например, плосковыпуклую линзу) по возможности с большим диамет­ром и малым фокусным расстоянием. Небольшой и в то же время достаточно яркий источник света можно получить, если, просверлив в большом экране 2 отверстие диаметром около 1 мм, укрепить перед ним кусочек матового стекла 3, освещенного сильной лампой с небольшого расстояния. Еще лучше сконцентрировать на матовом стекле свет от дугового фонаря. Эта «светящаяся точка» должна быть расположена на главной оптической оси линзы (рис. 228, а).

С помощью указанной линзы, на которую падают широ­кие световые пучки, не удается получить резкое изображе­ние источника. Как бы мы ни перемещали экран 4, на нем получается довольно расплывчатое изображение. Но если ограничить пучки, падающие на линзу, поставив перед ней кусок картона 5 с небольшим отверстием против централь­ной части (рис. 228, б), то изображение значительно улуч­шится: можно найти такое положение экрана 4, что изобра­жение источника на нем будет достаточно резким. Это наблюдение вполне согласуется с тем, что нам известно от­носительно изображения, получаемого в линзе с помощью узких приосевых пучков (ср. §89).

Заменим теперь картон с центральным отверстием кус­ком картона с небольшими отверстиями, расположенными вдоль диаметра линзы (рис. 229). Ход лучей, проходящих через эти отверстия, можно проследить, если слегка зады­мить воздух за линзой. Мы обнаружим, что лучи, проходя­щие через отверстия, расположенные на различном

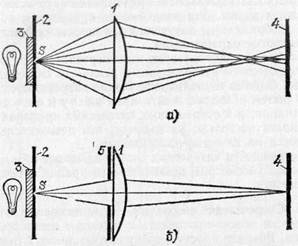
Рис. 228. Экспериментальное изучение сферической аберрации: а) лин­за, на которую падает широкий пучок, дает расплывчатое изображение; б) центральная зона линзы дает хорошее резкое изображение

расстоянии от центра линзы, пересекаются в разных точках: чем дальше от оси линзы выходит луч, тем сильнее он преломляется и тем ближе к линзе находится точка его пересечения с осью (рис. 230).

Таким образом, наши опыты показы­вают, что лучи, проходящие через от­дельные зоны линзы, расположен­ные на разных расстояниях от оси, дают изображения источника, лежащие на разных расстоя­ниях от линзы. При данном положении экрана разные зоны линзы дадут на нем: одни — более рез­кие, другие— более расплывчатые изоб­ражения источника, которые сольются в светлый кружок. В результате линза большого диаметра дает изображение точечного источника не в виде точки, а в виде расплывчатого светлого пятнышка.

Рис. 229. Экран с отверстиями для изучения сферичес­кой аберрации

Итак, при использовании широких световых пучков мы не получаем точечного изображения даже в том случае, когда источник расположен на главной оси. Эта погрешность оптических систем называется сферической аберрацией.

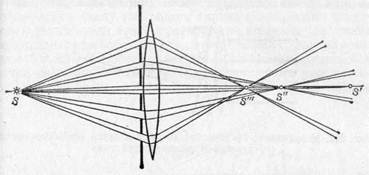
Рис. 230. Возникновение сферической аберрации. Лучи, выходящие из линзы на разной высоте над осью, дают изображения точки S в раз­ных точках S', S", S'"

Для простых отрицательных линз благодаря сфериче­ской аберрации фокусное расстояние лучей, проходящих через центральную зону линзы, также будет более значи­тельным, чем для лучей, проходящих через периферическую зону. Другими словами, параллельный пучок, проходя через центральную зону рассеивающей линзы, становится

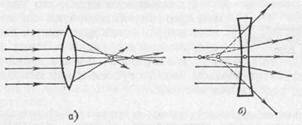
Рис. 231. Сферическая аберрация: а) в собирающей линзе; б) в рассеи­вающей линзе

менее расходящимся, чем пучок, идущий через наружные зоны. Заставив свет после собирающей линзы пройти через рассеивающую, мы увеличим фокусное расстояние. Это увеличение будет, однако, менее значительным для центральных лучей, чем для лучей периферических

(рис. 231).

Таким образом, более длинное фокусное расстояние со­бирающей линзы, соответствующее центральным лучам, увеличится в меньшей степени, чем более короткое фокусное расстояние периферических лучей. Следовательно, рассеи­вающая линза благодаря своей сферической аберрации

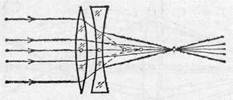
Рис. 232. Исправление сферической аберрации путем комбинирования собирающей и рассеивающей линз

выравнивает различие фокусных расстояний цент­ральных и периферических лучей, обусловленное сфериче­ской аберрацией собирающей линзы. Правильно рассчитав комбинацию собирающей и рассеиваю­щей линз, мы можем столь полно осу­ществить это выравнивание, что сфери­ческая аберрация системы из двух линз будет практически сведена к нулю (рис. 232). Обычно обе простые линзы склеи­ваются (рис. 233).

Из сказанного видно, что уничтоже­ние сферической аберрации осуществля­ется комбинацией двух частей системы, сферические аберрации которых взаим­но компенсируют друг друга. Аналогичным образом мы поступаем и при исправлении других недостатков системы.

Примером оптической системы с устраненной сферической абер­рацией могут служить астрономические объективы. Если звезда нахо­дится на оси объектива, то ее изображение практически не искажено аберрацией, хотя диаметр объектива может достигать нескольких де­сятков сантиметров.

§ 105. Астигматизм. Эта погрешность оптических систем проявляется в тех случаях, когда желают получить изобра­жение точки, находящейся на значительном расстоянии от главной оси системы, точнее, при использовании свето­вых пучков, составляющих значительный угол

Рис. 233. Склеен­ный астрономичес­кий объектив, ис­правленный на сфе­рическую аберра­цию

с главной осью (косые пучки). Важно отме­тить, что астигматизм остается даже при использовании узких световых пучков, а также может сохраняться в сис­темах, освобожденных от сферической аберрации.

Для наблюдения астигматизма выделим с помощью при­крывающего линзу картонного экрана с небольшим отвер­стием узкий пучок лучей и расположим источник так, чтобы он находился на побочной оси, составляющей с главной осью угол 30—40°. Мы обнаружим, что изображение светящейся точки на экране 4 (см. рис. 228) станет весьма расплывча­тым и будет иметь неправильную форму. Если мы начнем

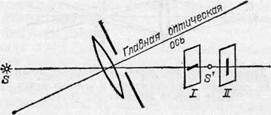
Рис. 234. Астигматизм линзы: изображения точки, лежащей на побоч­ной оси, представляют собой две взаимно перпендикулярные линии, лежащие в разных плоскостях.

медленно передвигать экран относительно линзы, то найдем, что имеются два положения экрана (I и II на рис. 234), в которых изображение довольно резкое. Однако, в от­личие от того случая, когда источник находился на главной оси линзы, изображение в указанных двух положениях экрана имеет вид не точки, а отрезка прямой. Направление отрезка в положении I перпендикулярно к направлению отрезка в положении II. Во всех остальных положениях экрана изображение расплывчатое, овальное [или круглое.

Таким образом, даже наилучшее изображение точки, не лежащей на главной оси линзы, представляет собой не точку, а две взаимно перпендикулярные и находящиеся в разных местах линии. Это и есть та погрешность оптиче­ских систем, которая носит название астигматизма.

Для исправления астигматизма приходится строить сложные оптические системы, состоящие из нескольких ча­стей, подобранных специальным образом так, чтобы они взаимно компенсировали астигматизм, обусловленный каж­дой из них. Системы с исправленным астигматизмом называются анастигматами *). Современные фотографические объективы, исправленные в отношении астигматизма, дают хорошее изображение при углах до 50—70°.

§ 106. Хроматическая аберрация. Поставим на пути све­товых лучей, выходящих из линзы 1, один раз красное стек­ло (пропускающее только красные лучи), другой раз синее стекло (пропускающее синие лучи). С помощью передвиж­ного экрана 2 (рис. 235) мы обнаружим, что изображения,

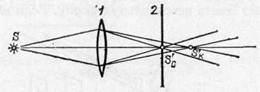
Рис. 235. Хроматическая аберрация: изображение точки S в синих

лучах S'_c не совпадает с изображением в красных лучах S'_к. Рисунок

Date: 2015-05-17; view: 2318; Нарушение авторских прав