Вектор, комплексное число и скалярное произведение

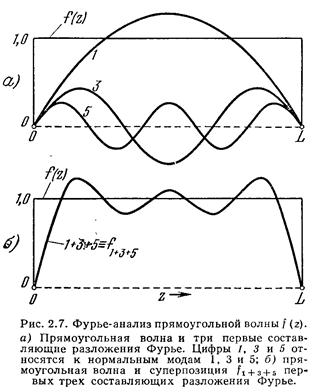
Самое сложное и красивое что нужно для понимания дальнейшего это разложение сложного движения на простые. Такое разложение называется разложением Фурье.

Понятие среднего.

Как правило, физическая величина получается в результате многих измерений и определяется как среднее значение. Напишем определение среднего через формулы.

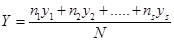
Здесь 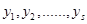результаты измерений, 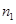это число выпадения результата 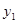, 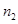число выпадения результата 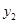, и так далее. Число 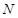это общее число испытаний, т.е.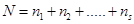

Можно немного преобразовать выражение для среднего

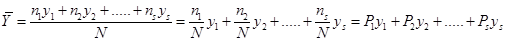
Здесь 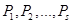это вероятности соответствующих результатов измерения. Эти вероятности как видно равны отношению числа случаев выпадения результата к общему числу испытаний. Для нас важно ещё следующие обстоятельства – каждая из вероятностей больше нуля, а сумма вероятностей не может быть больше единицы (единице сумма равна если учтены все возможные результаты измерений). Это можно легко показать и математически

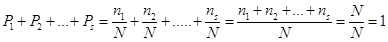
Теперь у нас есть всё, чтобы начать строить математическую теорию квантовой механики. Отправной точкой рассуждений будет понятие среднего и вероятности.

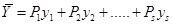
Как отмечалось выше, от вероятностей требуется, чтобы каждая из них была действительным числом, а их сумма не больше единицы. На самом деле возможен и «обратный» взгляд – всякая совокупность чисел с такими свойствами может рассматриваться как сумма вероятностей. В частности таким требованиям будет удовлетворять произведение комплексного числа на сопряжённое ему, если модуль этого числа не больше единицы.

Поэтому запишем

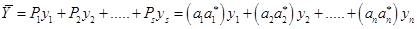
В этих шагах нет ничего особенного, это такая игра. Хотя…. Представление действительного числа с помощью комплексных можно рассматривать с философской точки зрения. Но не она тема настоящего материала. Следующим элементом игры будет умножение каждого из слагаемых на единицу. Но не просто так. Мы предположим, что у нас есть 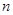векторов 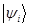для которых скалярное произведение равно единице: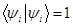

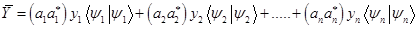
Здесь начинается самое интересное.

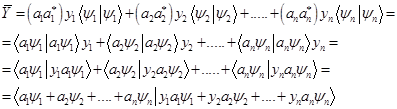
Здесь мы воспользовались свойством скалярного произведения .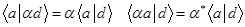

Далее мы внесём числа 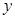под знак скалярного произведения. Для этого нам нужно будет связать вектора 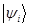условием перпендикулярност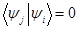и если 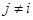. Тогда можно записать

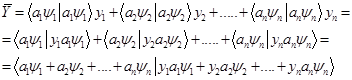
То, что это так можно увидеть прямыми выкладками (чтобы не затенять суть дела оставим только два вектора)

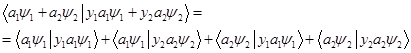
Мы видим, что у нас остаются только слагаемые, где под знаком скалярного произведения стоят одинаковые вектора. Другие слагаемые равны нулю в силу того что .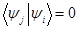

И наконец, завершающий штрих, но, пожалуй, самый хитрый (хоть и не хитрый сам по себе). Посмотрим ещё раз на запись . В левой его части стоит вектор 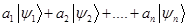. Это очень просто. А что же делать с правой частью 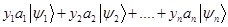? Это тоже вектор. Он получен из тех же векторов что и вектор слева. Будем считать, что он получен из этого левого вектора. Математики в таких случаях говорят, о воздействии оператора на вектор.

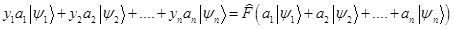
Фактически это равенство может служить определением оператора. Он таков что

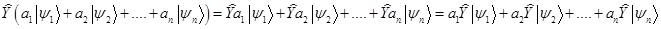
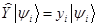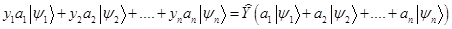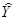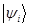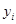Это свойство называется линейностью оператора, а сам он по этой причине называется линейным. Теперь мы наделим наш оператор специфическим свойством . Эти манипуляции можно воспринимать как игру. Мы просто захотели, чтобы было и дальше «подогнали» свойства оператора под своё желание. Оператор имеет простой смысл – он растягивает свой собственный вектор в раз.

После всех манипуляций запишем ещё раз последовательности и итог

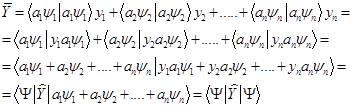
Вот собственно почти вся математика квантовой механики. Надо только разобраться в том, что мы «наделали» и дать какую-то интерпретацию введённым векторам, их перпендикулярности, оператору и числам .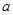

Перед тем как приступить к «следствию», поймём что получено. Мы начали с математического определения среднего, оно применимо к классической ситуации. Далее мы ввели вектора 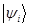, связанные отношением перпендикулярности. После этого мы представили среднее как скалярное произведение, что привело естественным образом к появлению линейного оператора .

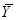Самое интересное, на мой взгляд, это функция 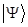. Во – первых мы видим что 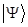,. Ведь, мы не делали каких-то особых предположений о природе измеряемой 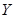. Следовательно, вместо оператора 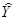мог бы стоять оператор сопоставляемой любой другой подлежащей измерению величины. В самом начале говорилось, о том, что в физике значение величин определяется как среднее значение результатов серии одинаковых измерений. Учитывая это, мы заключаем, что вектор 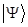полностью определяет среднее значение любой измеряемой величины. В ходе дальнейших рассуждений статус 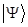будет повышен, до «нечто» полностью определяющее состояние системы.

Смысл вектора 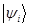мы можем понять, если рассмотрим такое состояние системы когда её можно описать только этим вектором.

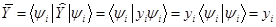
Т.е. среднее значение равно собственному числу 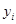оператора 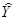. Т.к. среднее определяется на основе серии измерений, это означает, что все измерения дают только значение 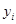и только его. Таким образом, мы приходим к выводу, что разрабатываемая нами теории подразумевает существование таких измерений, которые с достоверностью дают определённый результат.

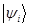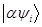Критично настроенный читатель, мог бы задаться вопросом о том, что было бы, если взять не , а , где 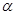произвольное число. В этом случае, мы получили бы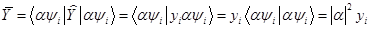

Этот результат говорит о том, что если описывать систему функцией 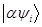, а не 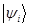, то значение среднего не измениться. Т.е. для теории значение имеет не величина вектора, а его направление. Это вообщем-то ожидаемо, т.к. измеряемая величина определяется тем во сколько раз соответствующий ей оператор растягивает свой собственный вектор.

Идём дальше. Установив смысл вектора 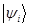можно спросить, а что с точки зрения измерений есть такой вектор 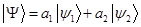. Ясно, что если система описывается такой функцией, результат не определён. Среднее будет равно 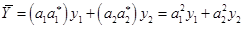- эта формула была у нас с самого начала. Там же вероятности были представлены как 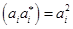. Т.е. вектор 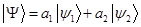описывает ситуацию, имеющуюся до измерения, когда они могут дать с вероятностью 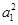результат 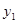, или результат 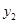с вероятностью .

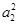Полученный результат формулируется как принцип суперпозиции состояний. Если система относительно грядущего измерения может находиться в состоянии 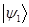, при котором измерение с достоверностью даёт значение 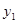, и в состоянии 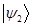с достоверностью приводящим к результату измерения 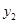, то вектор 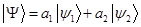имеет физический смысл. Этот смысл состоит в том что измерение может дать либо результат 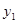(с вероятностью 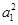), либо результат 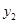(с вероятностью ).

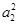Этот принцип играет очень большую роль в квантовой механике и можно сказать составляет её сердцевину. Он «отвечает» за интерференцию состояний и в частности за результаты знаменитого опыта с двумя щелями. Согласно этому принципу физическая величина не имеет определённого значения, пока не произошло измерение. Это находится в резком противоречии с классической физикой, которая предполагает, что измерения просто говорит нам о том, что было до измерения. Вот так высоты достижения человеческого разума, описываются простой математикой.

Т.е. под вектором описывающем систему надо миетНа языке геометрии Этот результат не противоречит тому, что существуют состояния, в которых измерения дают однозначный результат, но порождает вопрос о физической эквивалентности состояни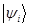й и 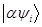, коль скоро применение правила среднего даёт для этих состояний различные результаты.

Хотя …. есть одно неявное предположение. Оно было сделано тогда, когда мы записали среднее как сумму, т.е. измеряемая принимает дискретный ряд значений. Это предположение не сильно ограничивает общность полученных выводов, хотя чтобы распространить их на непрерывные величины, нужна более тонкая и менее понятная для новичков математика. Поэтому этим мы заниматься не будем.

значение среднезначение среднего зависит определяется Как первый шаг для её понимания воспользуемся тем, что это вектор и представим себе, что это просто вектор 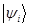. Тогда для среднего получим

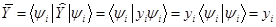
Мы видим что если системЭтот результат даёт возможность утверждать, что 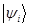это вектор описывающий такое состояние системы когда измерение с достоверностью даёт результат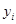

Немного терминологии. Вектор 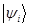, для которого 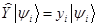называется собственными вектором оператора 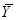принадлежащего собственному числу 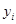. Мы знаем, что числа 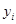это результаты измерений, т.е. они вещественны

Date: 2015-05-17; view: 948; Нарушение авторских прав