Пространство событий

Понятие о системе отсчёта. Траектория тела в системе отсчёта. Тело отсчёта и его связь с системой отсчёта. Физический эксперимент как множество относительных координат двух систем отсчёта. Примеры экспериментов. Пространство событий. Физика как теория относительности, построенная на анализе пространства событий. Классы систем отсчёта: инерциальные, ускоренные локально инерциальные первого рода, ускоренные локально инерциальные второго рода, ускоренные локально неинерциальные, ускоренные конформные. Примеры систем отсчёта.

Западный метод познания природы начинается с того, что выбирается своеобразная "точка зрения" исследователя – система наблюдения или система отсчёта. В трёхмерном пространстве механики Ньютона система отсчёта представляет собой три взаимно перпендикулярных направленных отрезка прямой линии с общим началом О (см. рис. 1). Изучая, например, траекторию летящего камня, брошенного параллельно земле, наблюдатель измеряет в разные моменты времени расстояния от начала О до летящего камня М. В результате этого эксперимента наблюдатель получает набор расстояний r в каждый момент времени.

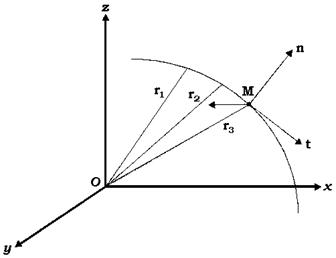
Рис. 1. Траектория камня, брошенного горизонтально поверхности земли. Наблюдатель измеряет расстояние r до камня в различные моменты времени t. Полученное множество относительных координат двух систем отсчёта содержит всю информацию о движении камня.

Анализируя полученные данные, он обнаруживает, что траектория камня описывается в данной системе наблюдения уравнением параболы.

Всякая реальная система отсчета связана с телом отсчета, в качестве которого может быть выбран любой физический объект – твердое тело, элементарная частица, волна света и т.д. Часто систему отсчета связываютсо стенами лаборатории, в которой идет эксперимент. В нашем конкретном случае одна система отсчета связана с поверхностью Земли, а другая с брошенным камнем. Поэтому данные наблюдателя представляют собой множество относительных координат двух систем отсчета. Это все что мы имеем в любом физическом эксперименте!

И. Кеплер, измеряя положение планет в различные моменты времени при движении их вокруг Солнца, обнаружил, что они движутся по эллипсам. Он работал со множеством относительных координат двух систем отсчета, одна из которых была связана с Солнцем, а другая с планетой. Оказывается, что множество относительных координат содержит всю информацию о гравитационном взаимодействии планеты и Солнца.

И. Ньютон догадался (наверное, в тот момент, когда яблоко упало ему на голову), что Земля притягивает массивные предметы с силой, вид которой можно определить, анализируя множество относительных координат падающего предмета и системы отсчета, связанной с Землей. Однако первоначально И. Ньютон исследовал движение планет, Луны и спутников Юпитера и установил, что их движение происходит под действием силы, величина которой пропорциональна произведению масс планет и обратно пропорциональна квадрату расстояния между ними.

Предположим, что мы изучаем движение заряженной частицы в электромагнитном поле. Опять вводятся две системы отсчета, одна из которых связана с лабораторией, а другая с заряженной частицей. Измеряя относительные координаты двух этих систем отсчета в различные моменты времени, мы получаем множество относительных координат, содержащее всю информацию об электромагнитном взаимодействии поля и частицы. Множества относительных координат, полученные в различных опытах, физики называют пространством событий, поскольку каждая точка этого пространства описывает некоторое элементарное событие. Таким образом, изучая гравитационные, электромагнитные, ядерные или какие-либо другие физические взаимодействия, мы в самой основе имеем дело с пространством событий изучаемого явления.

Из наших рассуждений следуют, по крайней мере, два вывода:

1. Любой физический эксперимент прямым или косвенным образом сводится к измерению относительных координат различных систем отсчета.

2. Физика – это теория относительности, изучающая природу посредством анализа пространства событий.

Исследуя пространство событий какого-либо явления, физик, создавая теорию явления, может использовать два крайних подхода:

а) либо, на основе анализа пространства событий, попытаться угадать уравнения, которые описывают явление, так, как это сделал Ньютон при создании своей теории гравитации (индуктивный подход);

б) либо проанализировать общие геометрические свойства пространства событий и получить физические уравнения из этого анализа, так, как это сделал Эйнштейн при создании общей теории относительности (дедуктивный подход).

Уравнения теории физического вакуума были получены дедуктивным путем. Для этого был выбран наиболее общий класс систем отсчета, который известен в настоящее время в физике, а затем исследованы геометрические свойства соответствующего пространства событий.

В настоящее время в физике известно пять классов систем отсчета:

1) инерциальные, которые движутся друг относительно друга с постоянной скоростью и без вращения;

2) ускоренные локально инерциальные первого рода, которые движутся ускоренно друг относительно друга без вращения, но локально ничем не отличаются от инерциальных систем (например, система отсчета, связанная со свободно падающим лифтом);

3) ускоренные локально инерциальные второго рода, которые движутся ускоренно относительно друг друга с вращением, но локально ничем не отличаются от инерциальных систем (например, система отсчета, связанная с центром масс однородного вращающегося диска);

4) ускоренные локально неинерциалъные (например, система отсчета, связанная с ускоряемой ракетными двигателями ракетой);

5) ускоренные конформные (такие системы связаны с физическими объектами, меняющими свои физические характеристики – массу, заряд и т. д. с течением времени).

Для каждого класса систем отсчета существует собственное, присущее только этому классу, пространство событий. Зная геометрические свойства пространства событий, можно найти, например, уравнения движения одной системы отсчета относительно другой. Поскольку система отсчета связана с каким-либо физическим телом, то мы сразу находим уравнения движения данного тела. Ясно, что ускоренное движение систем отсчета вызвано физическим взаимодействием тела отсчета с полем, в котором оно движется. Поэтому анализ пространства событий в этом случае позволяет найти не только уравнения движения тел отсчета, но и получить уравнения поля, под действием которого движется тело отсчета.

Date: 2015-05-09; view: 635; Нарушение авторских прав