
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Дуговой разряд
|
|
Дуговой разряд был открыт в 1802 году профессором физики В.Петровым. Он получил разряд в виде светящейся дуги, раздвигая два угольных электрода, предварительно приведенные в соприкосновение и присоединенные к мощной батарее гальванических элементов. В месте контакта сопротивление цепи высокое и происходит сильный разогрев, угли раскаляются. В результате возникает термоэлектронная эмиссия из катода. Электроны бомбардируют анод, образуя в нем углубление – кратер. Температура анода около 4000 К, при 20 атм она может подняться до 7000 К. Сила тока достигает десятков и сотен ампер, а напряжение на разрядном промежутке составляет несколько десятков вольт. Этот тип дугового разряда применяется для сварки и резки металлов.
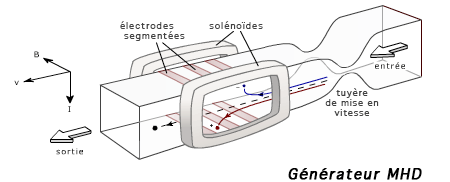
4. Плазмой называют сильно ионизованный газ, в котором концентрации положительных ионов и отрицательных электронов практически одинаковы. Плазма может быть высокотемпературной, полученной при высоких температурах термической ионизацией атомов, например, при термоядерном синтезе или в области дугового разряда. Газоразрядная низкотемпературная плазма возникает в электрическом поле.
Плазма имеет сходство с обычными газами и подчиняется газовым законам. Однако по электропроводности она приближается к металлам, для нее характерно сильное взаимодействие с электрическими и магнитными полями. Наличие подвижных разноименно заряженных частиц сопровождается их рекомбинацией и свечением.
Плазма используется в магнитогидродинамических (МГД) генераторах электрического тока. Низкотемпературная плазма применяется в газовых лазерах и плазменных телевизорах.
ЛЕКЦИЯ 5
Тема: Магнитное поле в вакууме и в веществе
Вопросы: 1) Действие магнитного поля на проводник с током. Магнитная
индукция.
2) Магнитное поле проводника с током. Закон Био-Савара-Лапласа.
3) Контур с током в магнитном поле.
4) Работа в магнитном поле.
1. В 1820 году Ампер открыл действие тока на магнитную стрелку: при пропускании тока через проводник расположенная рядом с ним магнитная стрелка поворачивается перпендикулярно к проводнику. Опыты Ампера показали, что проводники с током притягиваются друг к другу, если токи в них текут в одну сторону, и отталкиваются, если токи текут в противоположных направлениях. Таким образом, было установлено, что вокруг проводников с током существует магнитное поле. Обнаружить его можно по действию на проводник с током или постоянный магнит.
Пусть в однородном магнитном поле помещен прямой проводник длиной l с током I (рис.5.1).

Рис.5.1
Из опытов было установлено, что на проводник со стороны магнитного поля действует сила (сила Ампера)
F = I l B sinα,
где α – угол между проводником и направлением магнитного поля.
Направление силы можно определить по правилу левой руки (если четыре пальца расположить по направлению тока, а силовые линии магнитного поля будут входить в ладонь, то отогнутый большой палец покажет направление силы).
Если угол α между направлениями вектора В и тока в проводнике отличен от 90°, то для определения направления силы более удобно пользоваться правилом буравчика: воображаемый буравчик располагается перпендикулярно плоскости, содержащей вектор В и проводник с током, затем его рукоятка поворачивается от направления тока к направлению вектора В. Поступательное перемещение буравчика будет показывать направление силы. Правило буравчика часто называют правилом правого винта.
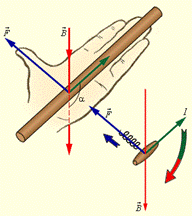
Рис.5.2
Сила Ампера зависит как от силы тока, так и от магнитного поля. Величина В называется магнитной индукцией и служит основной силовой характеристикой магнитного поля.
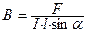
Если положить I = 1 А, l = 1 м, α = 90º, то B = F. Отсюда вытекает физический смысл В. Магнитной индукцией В называется физическая величина, численно равная силе, с которой магнитное поле действует на прямой проводник единичной длины с током единичной силы, расположенный перпендикулярно к силовым линиям магнитного поля.
Единица измерения магнитной индукции: [B] = Н/А·м = Тл (тесла).
Теперь становится понятным, почему два проводника с током притягиваются или отталкиваются: в зависимости от направления токов магнитное поле одного проводника выталкивает или втягивает другой проводник с током.
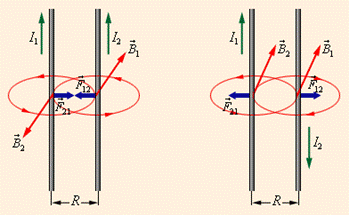
Рис.5.3
Магнитное поле удобно изображать с помощью силовых линий. Представление о таких линиях дает расположение железных опилок возле полюсов постоянного магнита.

Рис.5.4
Линией магнитной индукции (силовой линией) называется такая линия, проведенная в магнитном поле, касательная к которой в любой точке совпадает с вектором магнитной индукции в этой точке. Линии магнитной индукции замкнуты и охватывают проводник с током. Тот факт, что силовые линии не имеют начала, говорит об отсутствии магнитных зарядов.
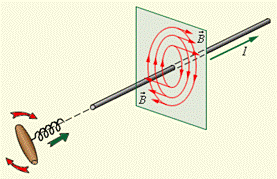
Рис.5.5
Направление силовых линий определяется по правилу буравчика: если ввинчивать буравчик так, чтобы винт двигался по направлению тока, то направление движения рукоятки совпадет с направлением силовой линии. Густота силовых линий пропорциональна величине магнитной индукции. Вблизи проводника с током магнитное поле неоднородно, чем ближе к проводнику, тем поле сильнее и силовые линии гуще. Однородное магнитное поле можно создать внутри длинной катушки с током.
Как видно из рисунка 5.6, магнитное поле катушки с током аналогично магнитному полю постоянного магнита, т.е. имеет «северный» конец N, из которого выходят силовые линии, и «южный» S, в который силовые линии входят. Индикаторные магнитные стрелки ориентируются по направлению касательных к линиям индукции.

Рис.5.6
Введем понятие – магнитный поток или поток Ф вектора магнитной индукции сквозь площадку S: Ф =В Scosα, где α – угол между нормалью (перпендикуляром) к площадке и магнитной индукцией В.
Единица измерения потока вектора магнитной индукции [Ф] = Тл·м² = Вб (вебер).

Рис.5.7
Если поле неоднородное и поверхность не плоская, то ее разбивают на бесконечно малые элементы dS так, что каждый элемент можно считать плоским, а поле однородным. Поток вектора магнитной индукции через элемент поверхности dФ = ВdScosα, а через всю поверхность

2. В результате многих опытов разных ученых был выведен закон Био – Савара – Лапласа, позволяющий рассчитывать магнитную индукцию полей, создаваемых проводниками с током.
 |
Пусть магнитное поле создается в вакууме элементом d l проводника с током I (рис.5.8).
 |
Рис.5.8
Тогда величина магнитной индукции в точке, удаленной от проводника на расстояние r определяется по закону Био-Савара-Лапласа, как
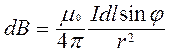 ,
,
где величина μ0 = 4π·10 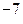 Гн/м называется магнитной постоянной.
Гн/м называется магнитной постоянной.
Направление вектора d В перпендикулярно плоскости, в которой лежат d l и r. Вектор d В направлен по касательной ксиловой линии, проведенной через рассматриваемую точку поля, в соответствии с правилом буравчика.
Для магнитного поля выполняется принцип суперпозиции: если имеется несколько проводников с током, то магнитная индукция в любой точке равна векторной сумме магнитных индукций, создаваемых в этой точке каждым проводником отдельно. Принцип суперпозиции справедлив и для элементов тока. Применяя совместно закон Био-Савара-Лапласа и принцип суперпозиции, можно определить магнитную индукцию различных проводников с током.

Пример. Магнитное поле в центре кругового проводника с током.
Рис.5.9
Магнитные индукции каждого элемента тока dl в центре направлены в одну сторону, перпендикулярную к плоскости контура проводника, и просто суммируются. Это можно понять, если провести через центр силовые линии каждого элемента проводника с током и построить к ним касательные. Направление магнитной индукции кругового проводника с током можно определять и по правилу буравчика: если ввинчивать буравчик, вращая рукоятку по направлению тока, то винт покажет направление магнитной индукции в центре.
Величину магнитной индукции определим по закону Био-Савара-Лапласа
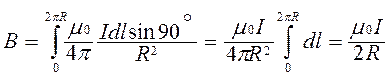
Создаваемые круговыми токами магнитные поля удобно описывать с помощью магнитного момента pm = IS, где I–ток в контуре, а S– площадь, обтекаемая током. За направление магнитного момента принимают направление нормали к плоскости витка, совпадающее с направлением вектора В в центре. Тогда 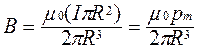
Можно показать, что магнитная индукция внутри длинной катушки с током (соленоида) B = μ0μnI, где n – число витков на единице длины катушки.
3. Поместим проводник, согнутый в виде прямоугольной рамки, в однородное магнитное поле.
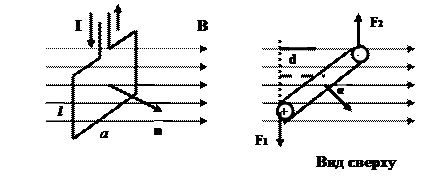
Рис.5.10
При протекании тока по проводнику на каждую его сторону действует сила со стороны магнитного поля. На верхнюю и нижнюю стороны действуют растягивающие контур силы. На боковые стороны действуют силы F1 = F2 = IB l sin90º, где l - длина боковой стороны. Каждая из этих сил создает вращающий момент М = Fd, где d – плечо силы.
Момент пары сил М = 2Fd.= 2IB l d. Из рис.5.10 видно, что 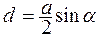 . Тогда M = IB la sinα или M = IBSsinα, где S – площадь рамки. Контур с током поворачивается до тех пор, пока его вращающий момент не станет равным нулю, т.е. станет равным нулю угол α. Таким образом, рамка с током в магнитном поле стремиться развернуться перпендикулярно к силовым линиям. Можно связать вращающий момент и магнитный момент контура с током
. Тогда M = IB la sinα или M = IBSsinα, где S – площадь рамки. Контур с током поворачивается до тех пор, пока его вращающий момент не станет равным нулю, т.е. станет равным нулю угол α. Таким образом, рамка с током в магнитном поле стремиться развернуться перпендикулярно к силовым линиям. Можно связать вращающий момент и магнитный момент контура с током
M = pmBsinα
Вращающий момент перестает действовать, когда магнитный момент контура с током ориентирован вдоль направления магнитной индукции поля.
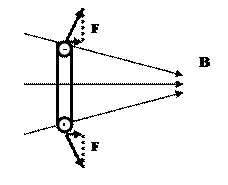 |
Можно показать, что вращающий момент действует в магнитном поле на замкнутый контур любой формы. Если поместить контур с током в неоднородное магнитное поле, то появляется составляющая силы Ампера, втягивающая контур в область более сильного поля.
 |
Рис.5.11
3. Магнитное поле может перемещать проводник с током, значит, поле совершает работу. Пусть прямой проводник длиной l под действием однородного магнитного поля переместится на расстояние dx в направлении, перпендикулярном к силовым линиям магнитного поля.

Рис.5.12
Работа dA = Fdx = I l Bdx. Так как произведение перемещения на длину проводника – это площадь dS, описываемая проводником при движении, то dA = IBdS, или dA = IdФ. Следовательно, работа по перемещению проводника в магнитном поле равна произведению силы тока в проводнике на магнитный поток, проходящий сквозь площадь, описываемую проводником при движении.
ЛЕКЦИЯ 6
Тема: Действие магнитного поля на движущийся заряд. Магнитное поле в
веществе
Вопросы: 1) Сила Лорентца.
2) Движение заряда в магнитном поле.
3) Магнитное поле в веществе.
4) Ферромагнетики.
1. Проводник с током создает в окружающем пространстве магнитное поле. Поскольку электрический ток представляет собой направленное движение заряженных частиц, то и любой движущийся заряд создает магнитное поле. Можно записать закон Био-Савара-Лапласа для одного заряда. Для этого преобразуем Idl = jSdl = nqvSdl = Nqv. Здесь j – плотность тока, n - число заряженных частиц в единице объема (концентрация частиц), v - скорость частиц. N – полное число частиц в отрезке dl проводника. Теперь магнитная индукция, создаваемая отрезком проводника с током, может быть представлена как
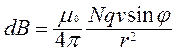 ,
,
а магнитная индукция поля, создаваемого в вакууме одним зарядом q на расстоянии r от заряда
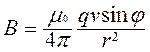
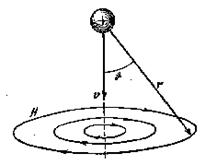
Рис.6.1
Направление силовых линий определяется по правилу буравчика.
Магнитное поле действует на ток, а значит и на каждый заряд должна тоже действовать сила. Выражение для нее получил Г.Лорентц.

Рис.6.2
На заряд q, движущийся в магнитном поле со скоростью v действует сила F = qvBsinα, где α – угол между направлением скорости и магнитной индукции. Направление силы для положительного заряда определяется по правилу левой руки или правого винта (вращать от v к B).
Таким образом, между движущимися зарядами существует как электрическое, так и магнитное взаимодействие.
2. Пусть частица с зарядом q и скоростью v влетает в однородное магнитное поле перпендикулярно к линиям магнитной индукции B (рис.6.3).
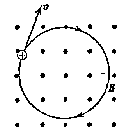
Рис.6.3
Сила, действующая на частицу, F = qvBsin90º. Сила перпендикулярна к скорости, значит, она не совершает работы и не меняет энергию и величину скорости частицы. Однако, сила, перпендикулярная к скорости, всегда вызывает центростремительное ускорение и движение по окружности, т.е.
qvB = mv²/R.
Радиус окружности траектории 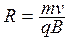 тем больше, чем больше скорость частицы. С увеличением магнитной индукции радиус уменьшается. Он зависит также от удельного заряда q/m частицы.
тем больше, чем больше скорость частицы. С увеличением магнитной индукции радиус уменьшается. Он зависит также от удельного заряда q/m частицы.
Период обращения частицы Т = 2πR/v. Подставив выражение для радиуса, получим 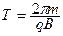 , т.е. период от скорости не зависит.
, т.е. период от скорости не зависит.
Пусть теперь заряженная частица влетает в магнитное поле под углом α к направлению магнитной индукции (рис.6.4).
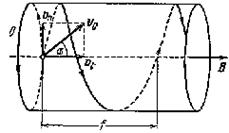
Рис.6.4
В этом случае скорость частицы v0 можно представить как векторную сумму тангенциальной скорости vt, направленной вдоль В, и нормальной скорости vn, перпендикулярной к В.
vt = v0 cosα, подставив эту скорость в выражение для силы Лорентца, получим F = qvtBsin0º, т.е. F = 0. Значит, вдоль силовой линии сила на частицу не действует и она движется равномерно и прямолинейно в этом направлении.
vn = v0 sinα,. сила Лоренца F = qvnBsin90º вызывает центростремительное ускорение и движение по окружности с радиусом 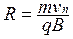 и периодом
и периодом 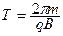 . В результате частица описывает траекторию в виде цилиндрической спирали с шагом (расстояние между витками спирали, на которое частица перемещается вдоль силовой линии, сделав один полный оборот) f = vt T.
. В результате частица описывает траекторию в виде цилиндрической спирали с шагом (расстояние между витками спирали, на которое частица перемещается вдоль силовой линии, сделав один полный оборот) f = vt T.
Закономерности движения заряженных частиц в магнитных и электрических полях используются в ускорителях, магнетронах, масс-спектрометрах и др.

Рис.6.5
3. Все вещества состоят из атомов и молекул, движение электронов в которых представляет собой замкнутые молекулярные токи. Каждый из этих токов создает магнитное поле, т.е. обладает магнитным моментом

где I – сила тока, S - площадь, обтекаемая током, n - единичный вектор нормали к плоскости витка с током.
В обычных условиях в результате теплового движения частиц магнитные моменты молекулярных токов разориентированы. Если поместить вещество в магнитное поле, то магнитные моменты частиц частично или полностью ориентируются вдоль внешнего магнитного поля, усиливая его (рис.6.6).
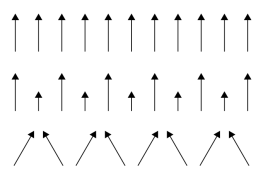
Рис.6.6
Вещества, способные намагничиваться, называются магнетиками. Магнитное состояние вещества характеризуется вектором намагничения, т.е. магнитным моментом единицы объема вещества
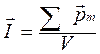
Единица измерения намагниченности – тесла. Для удобства рассмотрения ввели физическую величину Н – напряженность магнитного поля. Это силовая характеристика магнитного поля, связанная с магнитной индукцией соотношением 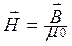 . Она характеризует магнитное поле в вакууме. Из опытов следует, что вектор намагничения пропорционален напряженности магнитного поля
. Она характеризует магнитное поле в вакууме. Из опытов следует, что вектор намагничения пропорционален напряженности магнитного поля 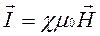 , где χ – магнитная восприимчивость вещества.
, где χ – магнитная восприимчивость вещества.
Полное значение магнитной индукции в магнетике равно
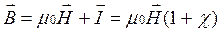
Значит, магнитная индукция в веществе  , где μ – магнитная проницаемость вещества. Она показывает, во сколько раз магнитное поле в веществе сильнее, чем в вакууме.
, где μ – магнитная проницаемость вещества. Она показывает, во сколько раз магнитное поле в веществе сильнее, чем в вакууме.
Есть некоторые вещества, у которых μ<1, их называют диамагнетиками (азот, вода, серебро, висмут). У них магнитный момент молекулярных токов устанавливается против поля, что объясняется появлением дополнительного вращения электронных орбиталей (прецессии) в магнитном поле.
У многих веществ μ >1, их называют парамагнетиками (кислород, алюминий и др.). У диамагнетиков и парамагнетиков магнитная проницаемость близка к единице, т.е. они намагничиваются слабо.
На границе раздела двух различных сред с разными значениями магнитной проницаемости линии магнитной индукции преломляются. Нормальная составляющая ветора магнитной индукции не меняется
Вn1 = Вn2
Касательные к границе раздела составляющие индукции испытывают скачок, причем
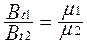
Из этих формул вытекает закон преломления линий индукции
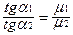 ,
,
где - угол между линиями магнитной индукции в среде 1 и нормалью к поверхности раздела, а - соответствующий угол в среде 2. Значит, линии индукции, входя в среду с большей магнитной проницаемостью, удаляются от нормали и сгущаются (рис.6.7).

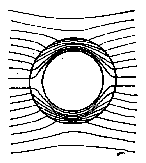
Рис.6.7 а – шар в магнитном поле (μ шара больше μ среды);
б - шар в магнитном поле (μ шара меньше μ среды);
в - железный цилиндр помещен в первоначально однородное
магнитноеполе.
4. Есть вещества, которые способны сильно намагничиваться, их магнитная проницаемость имеет величину порядка тысяч единиц и может достигать в специальных случаях миллиона. Такие свойства проявляет железо и его сплавы, поэтому этот класс веществ назвали ферромагнетиками. Свойства ферромагнетиков проявляют и другие металлы (табл.6.1).
Табл.6.1 Ферромагнитные металлы
| Металлы | ТК, К | Is0, 10  Тл Тл
|
| Fe (железо) | 1735,2 | |
| Co (кобальт) | ||
| Ni (никель) | 508,8 | |
| Gd (гадолиний) | ||
| Tb (тербий) | ||
| Dy (диспрозий) | 1991,8 | |
| Ho (гольмий) | 3054,6 | |
| Er (эрбий) | 19,6 | 1872,6 |
Ферромагнетики — вещества (как правило, в твёрдом кристаллическом или аморфном состоянии), в которых ниже определённой критической температуры ТК (точки Кюри) устанавливается дальний ферромагнитный порядок магнитных моментов атомов. Иными словами, ферромагнетик — такое вещество, которое при охлаждении ниже определённой температуры приобретает магнитные свойства. Выше точки Кюри ферромагнитные свойства исчезают.
Для ферромагнетиков характерна сильная ориентировка магнитных моментов атомов без внешнего магнитного поля. В результате обменного взаимодействия электронов образуются отдельные области самопроизвольного намагничения – домены. Такие домены были обнаружены на опыте с помощью порошковых фигур. На хорошо отполированную поверхность ферромагнетика помещают слой жидкости с порошком оксида железа. Крупинки оседают в местах неоднородности магнитного поля, то есть у стенок доменов, и границы доменов хорошо видны в микроскопе (рис.6.7).

а б в
Рис. 6.7 а – без магнитного поля; б – магнитное поле перпендикулярно плоскости чертежа; в – магнитное поле противоположного направления.
Направления намагничения в отдельных доменах различны и таковы, что полный магнитный момент ферромагнетика равен нулю. При включении внешнего магнитного поля растут домены, у которых вектор намагничения составляет острый угол с направлением внешнего магнитного поля, а объем доменов с тупым углом уменьшается.

Рис.6.8 Процесс намагничения ферромагнетика: а,б,в – смещение
границ; г и д – вращение вектора намагничения
В случае слабых полей (область 1) смещения границ обратимы и точно следуют за изменением поля. При увеличении поля смещения границ доменов делаются необратимыми и невыгодные домены исчезают. Затем при еще большем увеличении поля изменяется направление магнитного момента внутри домена. В очень сильном магнитном поле магнитные моменты всех доменов устанавливаются параллельно полю и ферромагнетик теперь намагничен до насыщения.
Все эти процессы намагничивания происходят с некоторой задержкой, то есть отстают от изменения поля, это явление называется гистерезисом (рис.6.8).
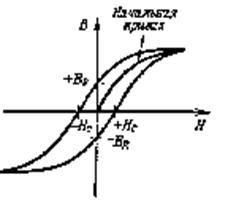
Рис.6.9 Петля гистерезиса
Если уменьшать магнитное поле, то когда поле Н станет равным нулю, в магнетике наблюдается остаточное намагничение +В. Чтобы полностью размагнитить магнетик, надо приложить магнитное поле противоположного знака –Нс. Это поле называют коэрцитивной силой ферромагнетика.
При циклическом перемагничении ферромагнетика изменение индукции в нем будет изображаться петлей гистерезиса. Работа при циклическом перемагничении пропорциональна площади петли гистерезиса. На нее затрачивается энергия магнитного поля, которая в конечном итоге превращается в тепло.
Вещества с большим остаточным намагничением (алнико, магнико и др.) называются магнитно-жесткими, они используются для изготовления постоянных магнитов. Алнико: 8% Al; 14% Ni; 24% Co;3% Cu;51% Fe.
Вещества с малым остаточным намагничением и малой коэрцитивной силой (пермаллой) называются магнитомягкими, они используются в устройствах переменного тока, например, в сердечниках трансформаторов. Пермаллой: 78% Ni; 22% Fe.
Ферромагнитные металлы нельзя использовать в радиотехнике высоких частот из-за их большой электропроводности и больших потерь энергии на вихревые токи. Для этой цели разработаны ферриты.
Ферриты, химические соединения окиси железа Fe2O3 с окислами других металлов. У многих ферритов сочетаются высокая намагниченность и полупроводниковые или диэлектрические свойства, то есть высокое удельное сопротивление (10² - 10  Ом.см), благодаря чему они получили широкое применение как магнитные материалы в радиотехнике, вычислительной технике.
Ом.см), благодаря чему они получили широкое применение как магнитные материалы в радиотехнике, вычислительной технике.
Поликристаллические ферриты производят по керамической технологии. Из ферритового порошка прессуют изделия нужной формы, которые подвергают затем спеканию при температурах от 900 до 1500 °C на воздухе или в специальной газовой атмосфере. Пленки феррит - фанатов и гексаферритов выращивают методом жидкостной эпитаксии из растворов в расплаве, а также путем разложения паров, например - дикетонатов металлов.
Для защиты приборов и оборудования от вредного влияния электромагнитного излучения других электрических и электронных приборов, а также природных явлений разработан широкий номенклатурный ряд материалов и конфигураций ферритовых сердечников (рис.6.10).


а б
Рис.6.10 а - ферритовые помехоподавляющие сердечники;
б - ферритовые поглощающие пластины для создания
безэховых камер и помещений, защищенных от
прослушивания.
ЛЕКЦИЯ 7
Тема: Электромагнитная индукция
Вопросы: 1) Явление электромагнитной индукции
2) Самоиндукция.
3) Энергия магнитного поля
1. Электрические токи создают вокруг себя магнитное поле. В 1831 году М. Фарадей открыл обратное явление: изменяющееся магнитное поле вызывает появление в проводниках тока. Это явление получило название электромагнитной индукции. На рис.7.1 показаны опыты

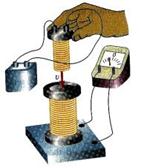
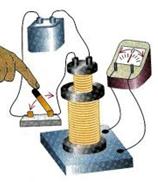
а б в
Рис. 7.1
Одна катушка соединена с источником тока, а вторая – с гальванометром. Если катушки неподвижны, то в цепи с гальванометром тока нет. При перемещении катушки или замыкании – размыкании цепи гальванометр показывает наличие тока. Направление индукционного тока при усилении магнитного поля противоположно направлению тока при ослаблении поля; если магнитное поле не меняется, то тока нет. Следовательно, опыты показывают, что причиной появления индукционного тока является изменение магнитного поля.
Закон Ленца: индукционный ток во всех случаях направлен таким образом, что его действие уменьшает причину, вызвавшую этот ток (рис.7.2).

Рис.7.2
Фарадей установил количественный закон электромагнитной индукции. Однако, в более общем случае закон был установлен Максвеллом, который проанализировал опыты Фарадея. Возникновение индукционного тока означает, что в проводнике появляется электродвижущая сила, и происходит это, когда проводник пересекает линии магнитной индукции.
Основной закон электромагнитной индукции: эдс электромагнитной индукции пропорциональна быстроте изменения магнитного потока через площадь, ограниченную контуром
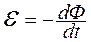 .
.
Знак минус соответствует закону Ленца. Как видно из рис.7.3, направление нормали n и выбранное положительное направление обхода контура l связаны правилом правого буравчика.
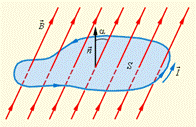
Рис.7.3 Магнитный поток через замкнутый контур.
Если магнитное поле увеличивается, т.е.  >0, то
>0, то  < 0, а значит и индукционный ток I< 0. Это означает, что направление индукционного тока противоположно выбранному положительному направлению.
< 0, а значит и индукционный ток I< 0. Это означает, что направление индукционного тока противоположно выбранному положительному направлению.
Явление электромагнитной индукции положено в основу работы генераторов электрического тока, электрических двигателей, трансформаторов и других электротехнических устройств.
Пример. Пусть в однородном магнитном поле находится проводник в виде замкнутого контура. Магнитный поток через контур Ф =В Scosα. Если контур вращается с постоянной угловой скоростью 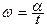 , то Ф =ВScosωt. Значит, при вращении контура магнитный поток через него меняется и в контуре возникает эдс индукции
, то Ф =ВScosωt. Значит, при вращении контура магнитный поток через него меняется и в контуре возникает эдс индукции
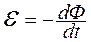 = В Sωsinωt,
= В Sωsinωt,
и течет синусоидальный (переменный) ток 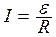 =
= 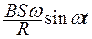 .
.
2. Пусть в проводнике в виде катушки течет ток (рис.7.4).
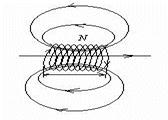
Рис.7.4
Величина магнитной индукции в любой точке поля пропорциональна величине тока, а значит, и магнитный поток, пронизывающий катушку, пропорционален току
Ф = LI.
Коэффициент пропорциональности L называется индуктивностью контура. Единицей индуктивности служит генри (Гн). 1 Гн = 1 Вб/А.
Индуктивность проводников зависит от их размеров, формы, от магнитной проницаемости среды. Так, индуктивность проводника в виде катушки равна
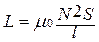 ,
,
где N - число витков катушки, l - длина катушки, S - площадь поперечного сечения катушки.
При изменении тока меняется магнитный поток через витки катушки, поэтому в катушке возникает эдс индукции и индукционный ток. Явление возникновение дополнительного индукционного тока в проводнике при всяком изменении основного тока называется самоиндукцией. Величина эдс самоиндукции
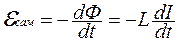
пропорциональна быстроте изменения тока.
Пусть имеется электрическая цепь (рис.7.5) с двумя лампочками Л1 и Л2, подключенными к источнику тока. К лампочке Л1 подключена последовательно катушка индуктивности.
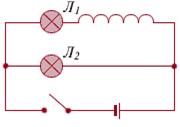
Рис.7.5
При разомкнутом ключе тока нет, и лампочки не светятся. Если ключ замкнуть, то медленнее загорается лампочка Л1., так как при нарастании тока в катушке индуктивности появляется эдс самоиндукции и течет индукционный ток, направленный против основного тока (препятствует нарастанию тока). При установившемся значении основного тока индукционный ток исчезает.
При размыкании ключа ток уменьшается и в катушке возникает индукционный ток такого же направления (препятствует уменьшению тока). Чем быстрее изменяется основной ток, тем больше величина индукционного тока (экстратока). Лампочка Л1 при этом ярко вспыхивает и гаснет позже Л2.
3. Рассмотрим электрическую цепь, изображенную на рис.7.6.
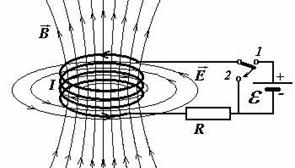
Рис.7.6
В положении 1 ключа через катушку течет постоянный ток и существует магнитное поле В этого тока. Если замкнуть ключ в положение 2, разомкнув 1, то через сопротивление потечет убывающий ток, поддерживаемый эдс самоиндукции. Работа тока за время dt равна dA =  сам q =
сам q =  сам Idt. Так как
сам Idt. Так как
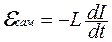 , то dA = -LIdI.
, то dA = -LIdI.
Проинтегрируем от до нуля и получим работу за время исчезновения магнитного поля
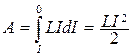
Работа идет на приращение внутренней энергии, то есть на нагревание сопротивления, проводов, катушки. Совершение работы сопровождается уменьшением магнитного поля, больше ничего не меняется, значит, работу совершает магнитное поле за счет своей энергии. Таким образом, энергия магнитного поля
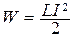
Можно показать, что 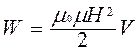 , где V – объем поля. Плотность энергии магнитного поля
, где V – объем поля. Плотность энергии магнитного поля
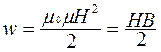
ЛЕКЦИЯ 8
Тема: Электромагнитные колебания
Вопросы: 1) Свободные колебания в контуре без активного сопротивления
2) Свободные затухающие электромагнитные колебания
3) Вынужденные электромагнитные колебания.
1. Цепь, содержащая индуктивность и емкость, называется колебательным контуром (рис.8.1). Сопротивление контура считаем пренебрежимо малым.

Рис.8.1
Если зарядить конденсатор и отключить источник, то вся энергия контура в начальный момент времени сосредоточена в электрическом поле конденсатора (рис.8.2).
t = 0 t = T/4 t = T/2 t = 3T/4 t = T

Рис.8.2
В первую четверть периода растет ток разрядки конденсатора, этот ток в катушке индуктивности создает возрастающий магнитный поток. Магнитный поток пронизывает витки катушки и порождает в них ток самоиндукции, направленный против основного тока (препятствует его возрастанию). В конце первой четверти периода ток достигает максимума Im и вся энергия теперь сосредоточена в магнитном поле. Заряда в конденсаторе нет, поэтому ток во второй четверти периода уменьшается, и ток самоиндукции меняет направление – теперь он направлен в ту же сторону, что и основной ток (препятствует его уменьшению). Этот ток самоиндукции перезаряжает конденсатор и в конце второй четверти периода энергия снова в электрическом поле, а ток равен нулю. Далее процесс повторяется в обратную сторону и за период заряд на обкладках конденсатора совершит полное колебание, как и ток в катушке индуктивности.
Из закона сохранения энергии следует, что электрическое и магнитное поля совершают одинаковую работу, т.е. U = 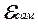 , где напряжение на конденсаторе U = q/C, а
, где напряжение на конденсаторе U = q/C, а 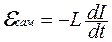 . Значит,
. Значит, 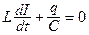 . Подставим
. Подставим 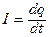 и разделим на L, получим
и разделим на L, получим
 , где обозначили
, где обозначили  .
.
Это дифференциальное уравнение является уравнением свободных незатухающих электромагнитных колебаний в контуре. Решение этого уравнения q = q0cos(ωt +α 0) описывает гармонические колебания заряда на обкладках конденсатора. Амплитуда заряда q0, циклическая частота ω = 2πν, частота колебаний  , период колебаний
, период колебаний 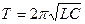 .
.
Напряжение на конденсаторе создается зарядом и изменяется так же:
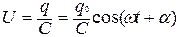 = Umcos(ωt+α), где Um - амплитуда напряжения.
= Umcos(ωt+α), где Um - амплитуда напряжения.
Сила тока в контуре
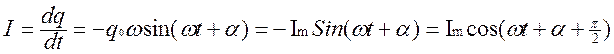
где Im - амплитуда тока, α – начальная фаза. Из соотношения фаз видно, что ток опережает напряжение на конденсаторе на π/2. При нулевом напряжении ток максимальный.
Из сравнения амплитуд тока и напряжения вытекает 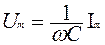 , т.е. амплитуды связаны законом Ома, где
, т.е. амплитуды связаны законом Ома, где  представляет собой емкостное сопротивление цепи.
представляет собой емкостное сопротивление цепи.
Напряжение на катушке индуктивности должно быть равно ЭДС самоиндукции и противоположно к ней направлено:
U = - 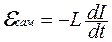 = LωImcos (ωt+α) = LωImsin (ωt+α +π/2)
= LωImcos (ωt+α) = LωImsin (ωt+α +π/2)
Из соотношения фаз видно, что ток в катушке индуктивности отстает от напряжения на π/2. Амплитуды тока и напряжения связаны соотношением Um=Im. В этом случае XL = ωL представляет собой индуктивное сопротивление цепи.
2. Всякий реальный колебательный контур обладает сопротивлением R (рис.8.3) и при протекании тока в проводниках выделяется джоулево тепло. Поэтому, если один раз зарядить конденсатор, то запасенная энергия расходуется на тепло и колебания затухают.
3.
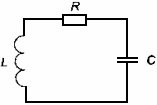
Рис.8.3
Так как источника ЭДС в цепи нет, то применяя второй закон Кирхгофа к цепи, получим UL+UR+UC = 0. После подстановки получаем
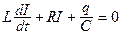
Выразим ток через заряд и разделим уравнение на L. Получим дифференциальное уравнение свободных затухающих колебаний
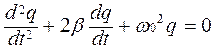
Здесь 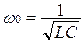 собственная частота колебательного контура,
собственная частота колебательного контура, 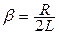 коэффициент затухания. Решение полученного уравнения (рис.8.4)
коэффициент затухания. Решение полученного уравнения (рис.8.4)
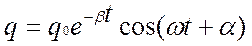 , где q0 – величина заряда в начальный момент времени, частота затухающих колебаний
, где q0 – величина заряда в начальный момент времени, частота затухающих колебаний 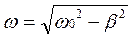 , т.е.
, т.е. 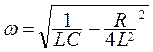 .
.
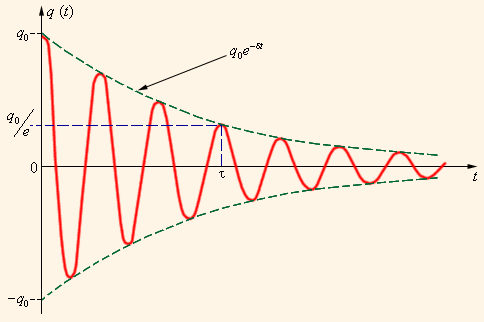
Рис.8.4
Время затухания τ – это время, за которое заряд на обкладках конденсатора уменьшается в е = 2,7 раз. τ = 1/β, т.е. τ = 2L/R.
3. Колебания, происходящие в электрической цепи под действием внешней периодической эдс, называются вынужденными. Это действие может быть оказано через индуктивную связь двух катушек индуктивности (взаимная индукция) или непосредственным включением переменного напряжения
U = Umcosωt в колебательный контур (рис.8.5).

U
Рис.8.5
Применяя второй закон Кирхгофа к цепи, получим UL+UR+UC = Umcosωt, или  . Здесь ω – частота переменного напряжения,
. Здесь ω – частота переменного напряжения, 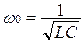 - собственная частота колебательного контура,
- собственная частота колебательного контура, 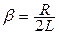 - коэффициент затухания.
- коэффициент затухания.
Решение уравнения дает q = q mcos (ωt – φ), где амплитуда заряда
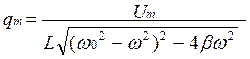 ;
; 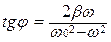 .
.
При некоторой частоте внешнего напряжения амплитуда колебаний резко возрастает, т.е. возникает резонанс. Чтобы определить резонансную частоту, нужно найти максимум функции q(ω), т.е. минимум выражения под корнем в знаменателе. Для этого продифференцируем выражение и получим
-4(ω0² – ω²) ω + 8β²ω = 0. Уравнение имеет три решения для ω: ω = 0 и 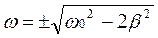 . ω = 0 соответствует максимуму знаменателя, а отрицательная частота не имеет смысла, поэтому
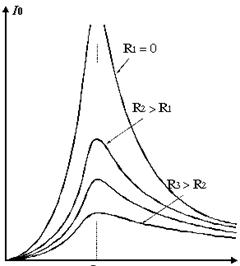
. ω = 0 соответствует максимуму знаменателя, а отрицательная частота не имеет смысла, поэтому  . Чем меньше β, т.е. меньше сопротивление контура, тем выше и острее максимум резонансной кривой для тока (рис.8.6).
. Чем меньше β, т.е. меньше сопротивление контура, тем выше и острее максимум резонансной кривой для тока (рис.8.6).
Уравнение для тока получим, продифференцировав выражение для заряда: I = - ω q msin (ωt – φ) или I = Imcos (ωt – φ +π/2). Ток и заряд изменяются в противофазе, когда заряд на конденсаторе достигает максимума, ток в цепи равен нулю и наоборот.
 ω
ω
ωрез
Рис.8.6
Для напряжений в каждый момент времени выполняется соотношение
UL+UR+UC = Umcosωt.
Напряжение на резисторе UR = IR, UR = RImsin (ωt – φ). Ток в резисторе изменяется в одной фазе (синфазно) с напряжением.
Напряжение на конденсаторе
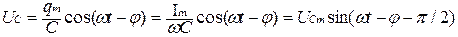 .
.
Напряжение на конденсаторе и ток также изменяются в противофазе, причем ток опережает напряжение на π/2.
Напряжение на индуктивности

В этом случае ток отстает от напряжения на π/2.
Для наглядного решения уравнения вынужденных колебаний можно использовать метод векторных диаграмм. На векторной диаграмме колебания определенной заданной частотыω изображаются с помощью векторов. Длины векторов на диаграмме равны амплитудам колебаний, а наклон к горизонтальной оси определяется фазами колебаний φ1 и φ2. Взаимная ориентация векторов определяется относительным фазовым сдвигом Δφ = φ1 – φ2. Вектор, изображающий суммарное колебание, строится на векторной диаграмме по правилу сложения векторов.
Для того, чтобы построить векторную диаграмму напряжений и токов при вынужденных колебаниях в электрической цепи, нужно знать соотношения между амплитудами токов и напряжений и фазовый сдвиг между ними для всех участков цепи. На рис.8.7 показана векторная диаграмма для напряжений на участках рассмотренного колебательного контура (амплитуда тока обозначена I0).

Рис. 8.7 Векторная диаграмма для последовательной RLC -цепи
Амплитуды токов и напряжений связаны законом Ома, поэтому XL = ωL называют индуктивным сопротивлением, а  - емкостным сопротивлением. Полное электрическое сопротивление последовательной RLC- цепи синусоидального тока
- емкостным сопротивлением. Полное электрическое сопротивление последовательной RLC- цепи синусоидального тока 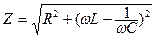 .
.
ЛЕКЦИЯ 9
Тема: Теория Максвелла. Электромагнитные волны.
Вопросы: 1) Теория Максвелла
2) Электромагнитные волны, получение и свойства
3) Шкала электромагнитных волн
1. В шестидесятых годах девятнадцатого века профессор кембриджского университета Джеймс Максвелл опубликовал «Динамическую теорию поля», созданную на основе анализа всех открытых к тому времени явлений электричества и магнетизма. Максвелл пришел к выводу, что в явлении электромагнитной индукции наличие проводника не имеет существенного значения (ЭДС индукции не зависит от природы проводника), и сформулировал первое основное положение своей теории: всякое изменение магнитного поля вызывает появление вихревого электрического поля (рис.9.1).
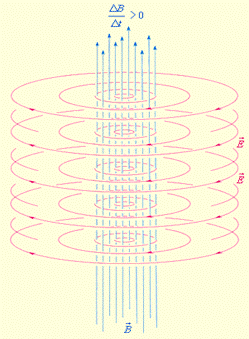
Рис. 9.1
Электрическое поле динамическое и вызывает в любом проводнике движение электронов по замкнутым траекториям. Значит, вихревое электрическое поле выполняет роль сторонней силы в выражении электродвижущей силы для вихревых токов в проводниках
 =
= 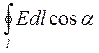
Эта ЭДС вызвана изменением магнитного поля 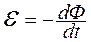 , поэтому математическое выражение первого основного положения теории Максвелла имеет вид
, поэтому математическое выражение первого основного положения теории Максвелла имеет вид
 =
= 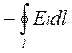
Вихревые токи в массивных проводниках сопровождаются выделением большого количества джоулева тепла, поэтому нашли полезное применение в индукционных печах. В электротехнических устройствах (трансформаторах, двигателях, генераторах) на вихревые токи бесполезно тратится электрическая энергия, поэтому токи называют паразитными и подавляют их, набирая магнитопроводы (сердечники, корпуса) из тонких пластин, изолированных лаком.
Максвелл высказал гипотезу, что магнитное поле порождается не только токами, текущими в проводниках, но и переменными электрическими полями
в диэлектриках или вакууме. Для установления количественных соотношений между изменяющимся электрическим полем и вызываемым им магнитным полем Максвелл ввел в рассмотрение так называемый ток смещения.
Рассмотрим цепь переменного тока, содержащую конденсатор (рис.9.2).

Рис.9.2
Между обкладками заряжающегося и разряжающегося конденсатора имеется переменное электрическое поле, замыкающее электрическую цепь. Если включить в цепь лампочку, то она будет гореть. Через конденсатор «протекает» ток смещения. Током смещения была названа Максвеллом величина, пропорциональная скорости изменения электрического поля во времени. Ток смещения возбуждает такое же магнитное поле, что и ток проводимости в проводах (позднее это было подтверждено экспериментально) (рис.9.3).
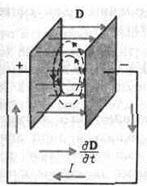
Рис.9.3
Полный ток в цепи переменного тока, равный сумме тока проводимости и тока смещения, всегда является замкнутым. Плотность полного тока  , где j – плотность тока в проводах, D – вектор электрического смещения поля в диэлектрике конденсатора. Полный ток через площадь S
, где j – плотность тока в проводах, D – вектор электрического смещения поля в диэлектрике конденсатора. Полный ток через площадь S
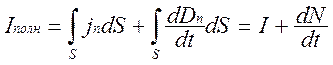 ,
,
где N –поток вектора электрического смещения через площадь S.
Второе основное положение теории Максвелла: переменное во времени электрическое поле вызывает появление вихревого магнитного поля
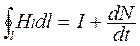
Таким образом. Максвелл показал, что электрическое и магнитное поля неразрывно связаны в единое электромагнитное поле, которое в частных статических ситуациях проявляется как электрическое или магнитное поле. На этой основе Максвелл создал единую теорию всех электрических и магнитных явлений.
Полная система уравнений теории включает, помимо двух основных положений, теорему Гаусса: поток вектора смещения через замкнутую поверхность равен заряду, охватываемому поверхностью
 ;
;
Поток вектора магнитной индукции через замкнутую поверхность равен нулю (магнитных зарядов не существует)
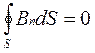
В систему уравнений входят также уравнения, включающие характеристики вещества – диэлектрическую и магнитную проницаемости, проводимость
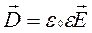
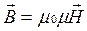
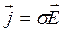
Теория Максвелла объяснила все открытые ранее явления электричества и магнетизма и предсказала существование электромагнитных волн. В настоящее время она является теоретической основой многих прикладных наук и технических направлений.
2. Из уравнений Максвелла были получены волновые уравнения для векторов Е и В. В случае однородной нейтральной непроводящей среды с постоянными проницаемостями ε и μ
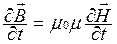 ,
, 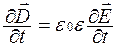
В результате математических преобразований из этих выражений получаются волновые уравнения
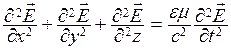 ,
,
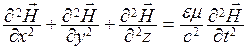 ;
;
Здесь вместо двух постоянных ε0 и μ0 введена одна постоянная с = 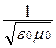 , причем коэффициент в правой части уравнений имеет смысл квадрата скорости волны, т.е. скорость электромагнитной волны
, причем коэффициент в правой части уравнений имеет смысл квадрата скорости волны, т.е. скорость электромагнитной волны
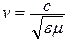
На практике впервые получил электромагнитные волны Генрих Герц в 1888 году. Герц не только экспериментально доказал существование электромагнитных волн, но впервые начал изучать их свойства – поглощение и преломление в разных средах, отражение от металлических поверхностей и т. п. Опыты Герца сыграли решающую роль для доказательства и признания электромагнитной теории Максвелла. Через семь лет после этих опытов электромагнитные волны нашли применение в беспроводной связи (А. С. Попов, 1895 г.).
В начале двадцатого века многими учеными разных стран проводились опыты по определению скорости света, ее величина оказалась равной с. В вакууме с=3·10  м/с.
м/с.
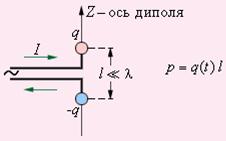
Для создания электромагнитной волны надо, чтобы существовало быстро изменяющееся электрическое или магнитное поле. Простейшей системой, излучающей электромагнитные волны, является небольшой по размерам электрический диполь, дипольный момент которого быстро изменяется во времени (рис.9.4). Это может быть небольшая антенна (в опыте Герца – вибратор), система ядро - электрон в атоме также представляет собой диполь (рис.9.4 а).
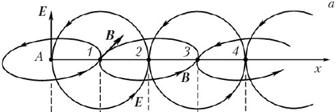
Вдоль оси диполя существует изменяющееся электрическое поле Е, котороепорождает вихревое магнитное поле В. Магнитное поле, в свою очередь, порождает вихревое электрическое поле и так далее. Этот процесс в виде электромагнитной волны распространяется вдоль оси Х со скоростью v, в направлении, перпендикулярном оси диполя (рис.9.4 б).
 а
а
б
Рис. 9.4
Обычно электромагнитную волну представляют в графическом виде (рис.9.5).
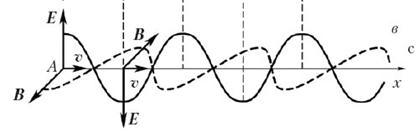
Рис.9.5
Электрическое и магнитное поля в любой момент времени нарастают или уменьшаются одновременно, т.е. колеблются синфазно во взаимно перпендикулярных плоскостях. Уравнения колебания векторов Е и В получены как решения дифференциального волнового уравнения
E = E0 cos (ωt – kx)
B = B0 cos (ωt – kx)
здесь k = ω/v или k = 2π/λ называется волновым числом.
В электромагнитной волне происходят взаимные превращения электрического и магнитного полей. Эти процессы идут одновременно, и электрическое и магнитное поля выступают равноправно. Поэтому объемные плотности электрической и магнитной энергии равны друг другу: wэ = wм:
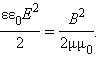
Электромагнитные волны переносят энергию. При распространении волн возникает поток электромагнитной энергии. Если выделить площадку S, ориентированную перпендикулярно направлению распространения волны, то за малое время Δt через площадку протечет энергия ΔWэм, равная
ΔWэм = (wэ + wм)v SΔt
Скорость электромагнитной волны 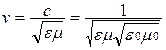
Плотностью потока или интенсивностью I называют электромагнитную энергию, переносимую волной за единицу времени через поверхность единичной площади:
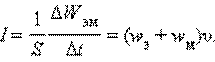
Подставляя выражения для wэ, wм и v, можно получить: 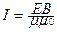
Поток энергии в электромагнитной волне можно задавать вектором  ,
,
направление которого совпадает с направлением распространения волны, а модуль равен EB / μμ0. Этот вектор называют вектором Пойнтинга.
Плотность потока энергии в СИ измеряется в Вт/м2.
3. Электромагнитные волны классифицируются по длине волны λ или связанной с ней частотой υ волны. Спектром электромагнитных волн называется полоса частот электромагнитных волн, существующих в природе.
Электромагнитные волны излучаются антеннами или атомами вещества. Длина волны излучения составляет обычно половину размера излучателя, поэтому спектр электромагнитного излучения достаточно широк (рис.9.5).

Рис.9.5
.
Спектр электромагнитного излучения в порядке увеличения частоты составляют:
- радиоволны;
- инфракрасное излучение;
- оптическое излучение;
- рентгеновское излучение;
- гамма-излучение.
Между различными участками электромагнитного спектра нет резких границ.
Радиоволны излучаются и принимаются антеннами и делятся на:
• Длинные волны в интервале длин волн от десятков км до 1км (частота в диапазоне от 3 кГц до 300кГц);
• Средние волны в интервале длин волн от1км до 100м (частота в диапазоне 3 105 Гц – 3МГц);
• Короткие волны в интервале длин волн от 100м до 10м (частота в диапазоне 3106Гц-3107Гц);
• Ультракороткие волны (УКВ) с длиной волны меньше 10м (частота больше 3107гц=30Мгц).
Волны с длиной волны меньше, чем 1м (частота больше 300мгц) называются микроволнами или волнами сверхвысоких частот (СВЧ - волны).
Оптическая область спектра включает инфракрасное (ИК) излучение, видимый свет и ультрафиолетовое (УФ) излучение. Оптическое излучение испускается при переходах в атомах электронов внешних орбиталей.
Оптический спектр занимает диапазон длин электромагнитных волн в интервале от 2·10-6м= 2мкм до 10-8м=10нм (по частоте от1,5·1014Гц до 3·1016Гц). Верхняя граница оптического диапазона определяется длинноволновой границей инфракрасного диапазона, а нижняя коротковолновой границей ультрафиолета.
Рентгеновское излучение возникает при торможении быстрых заряженных частиц (электронов, протонов и пр.), а также в результате переходов электронов внутренних электронных оболочек атомов. Рентгеновское излучение составляют электромагнитные волны с длиной от 50 нм до 10-3нм.
Гамма-излучение является следствием явлений, происходящих внутри атомных ядер, а также в результате ядерных реакций. Гамма излучение составляют электромагнитные волны с длиной волны меньше 10-2 нм.
ЛЕКЦИЯ 10
Тема: Фотометрические характеристики света. Законы геометрической оптики.
Вопросы: 1) Фотометрические характеристики света.
2) Законы геометрической оптики.
3) Линзы
1. Свет представляет собой видимый участок спектра электромагнитных волн, длины волн которых занимают интервал от 0.4 мкм до 0.76 мкм. Каждой спектральной составляющей оптического излучения может быть поставлен в соответствие определённый цвет. Излучение одного цвета (одной длины волны) называется монохроматическим. Цвет излучения изменяется по мере уменьшения его длины волны (увеличения частоты) следующим образом: красный, оранжевый, желтый, зеленый, голубой, синий, фиолетовый.
Красный свет, соответствующий наибольшей длине волны, определяет красную границу видимого спектра. фиолетовый свет - соответствует фиолетовой границе.
Белый естественный свет – содержит всевозможное излучение разных длин волн. Опыт показывает, что физиологическое, фотохимическое действие производит электрическое поле волны, оно же вызывает колебания в приемной антенне. Поэтому плоскую электромагнитную световую волну обычно представляют уравнением E = Acos (wt +kx), где волновое число k = 2π/λ. Плоской называют волну, порождаемую линейным протяженным источником света и имеющую прямолинейный фронт волны при своем распространении. От точечного источника света распространяется во все стороны сферическая волна, описываемая уравнением 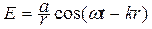 , где a – начальная амплитуда, а r – расстояние от источника.
, где a – начальная амплитуда, а r – расстояние от источника.
У плоской волны амплитуда постоянная, а у сферической убывает по мере удаления от источника. На достаточно удаленном расстоянии от точечного источника сферическая волна становится все более плоской, поэтому за основу берется уравнение плоской волны.
Линии, вдоль которых распространяется световая энергия, называются лучами. Интенсивность света в данной точке пространства – это среднее значение (по времени) потока энергии, переносимой световой волной.
Световой поток Ф – это энергия, излучаемая источником света в единицу времени
Ф = W/t.
Единица светового потока – люмен лм (энергетическая – ватт).
Сила света численно равна потоку излучения источника света, приходящемуся на единицу телесного угла
I = dФ/dΩ
или для точечного изотропного источника света I = Ф /4π, где Ф – полный световой поток во всех направлениях. Единица силы света – кандела кд (ватт на стерадиан – Вт/ср).
Яркость источника света – отношение силы света к площади светящейся поверхности
L = dI/dt.
Единица измерения яркости – кд/м².
Освещенность численно равна световому потоку, падающему на единицу поверхности
E = dФ/dS
Измеряется в люксах лк. Освещенность площадки светом, падающим под углом α к нормали к площадке, расположенной на расстоянии r от источника света (рис.10.1), можно выразить через силу света



Рис. 10.1
2. Еще во времена ранней истории были открыты законы лучевой, или так называемой геометрической, оптики.
Закон прямолинейного распространения света: в однородной среде свет распространяется по прямым линиям. Опытным доказательством этого закона служат резкие тени, даваемые предметами в солнечный день.
Закон независимости световых лучей: световые лучи при пересечении не смешиваются, распространяются независимо друг от друга. Отступление от этого закона обнаруживается только для мощных лазерных лучей.
Закон отражения света: угол падения света α на поверхность равен углу отражения γ, причем, луч падающий, луч отраженный и перпендикуляр (нормаль) к поверхности в точке падения лежат в одной плоскости (рис.10.2).

Рис.10.2
Закон отражения света объясняет, как получается изображение в зеркале.
Закон преломления света: угол падения α и угол преломления β (рис.10.2) связаны соотношением
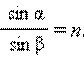
Относительный показатель преломления (второй среды относительно первой) 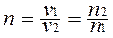 , где v1 и v2 – скорость света в первой и во второй среде, а n1 и n2 –абсолютные показатели преломления двух сред. Абсолютный показатель преломлени
, где v1 и v2 – скорость света в первой и во второй среде, а n1 и n2 –абсолютные показатели преломления двух сред. Абсолютный показатель преломлени
Date: 2015-05-09; view: 2346; Нарушение авторских прав