Теплообмен при поперечном обтекании труб жидкостью

Одиночные трубы. Теплообмен при поперечном обтекании жидкостью трубы (рис. 11.) зависит от гидродинамической картины жидкости около поверхности. Обтекание трубы может быть плавным – безотрывным и отрывным. Плавное безотрывное обтекание трубы наблюдается только при .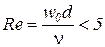

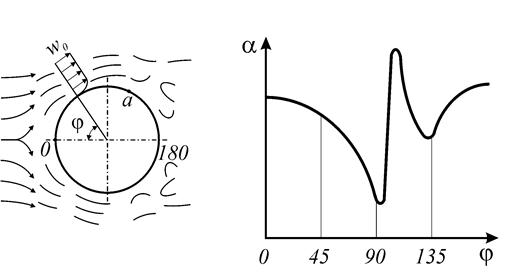
Рис. 11. Схема движения и график изменения коэффициента

теплоотдачи при поперечном обтекании трубы

При Re>5 пограничный слой, образующийся на передней половине трубы, в кормовой части отрывается от поверхности; позади трубы образуются два симметричных вихря.

В соответствии с этим меняется коэффициент теплоотдачи по поверхности трубы. В лобовой части он наибольший, далее по периметру трубы коэффициент теплоотдачи α падает и достигает минимального значения в точке отрыва потока (точка а). В вихревой части коэффициент теплоотдачи увеличивается.

Для определения коэффициента теплоотдачи при поперечном обтекании одиночной трубы используют следующие уравнения подобия:

при Re = 5 – 10³

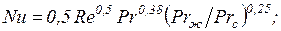(131)

при Re = 10³ – 2·10⁵

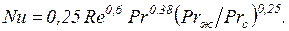(132)

За определяющий линейный размер принят внешний диаметр трубы; за определяющую температуру – температура набегающего потока; скорость жидкости отнесена к самому узкому сечению канала, в котором расположена труба.

Формулы (131 и 132) справедливы при условии, что угол между направлением потока и осью трубы, называемой углом атаки, равен 90º. При уменьшении угла атаки уменьшается. Если угол атаки меньше 90º, то полученный коэффициент теплоотдачи необходимо умножить на поправочный коэффициент 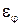, приближенные значения множителя 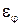можно определить по формуле

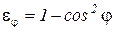. (133)

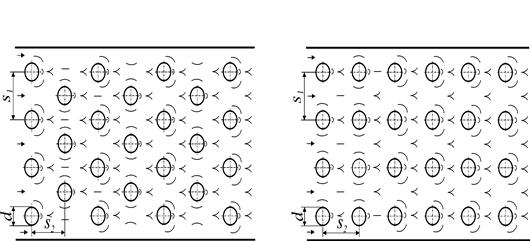
Пучки труб. При поперечном обтекании потоком жидкости пучка труб интенсивность теплоотдачи зависит не только от факторов, влияющих на теплоотдачу одиночной трубы, но и от взаимного расположения труб в пучке, а также от плотности пучка. Обычно применяют коридорное (по вершинам квадрата) и шахматное (по вершинам треугольника) расположение труб в пучке (рис. 12).

аб

Рис. 12. Схемы расположения труб в пучках: (а) – шахматное; (б) – коридорное расположение (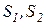 – поперечный и продольный соответственно шаги труб)

Плотность расположения труб в пучке характеризуется соотношениями между поперечным шагом S₁, продольным шагом S₂ и внешним диаметром труб d.

Исследованиями установлено, что теплоотдача труб второго и третьего рядов постепенно возрастает по сравнению с теплоотдачей первого ряда. Это объясняется увеличением турбулентности потока при прохождении его через пучок труб. Начиная с третьего ряда поток практически стабилизируется, поэтому и средний коэффициент теплоотдачи для всех последующих рядов сохраняет постоянное значение. Если значение коэффициента теплоотдачи третьего ряда (и последующих рядов) α₃, то в коридорном пучке для первого и второго ряда труб коэффициент теплоотдачи α₁=0,6 α₃ и α₂ =0,9 α₃, при

шахматном расположении α₁=0,6 α₃ и α₂ =0,7 α₃. Средний коэффициент теплоотдачи для третьего и последующих рядов определяется из уравнения подобия

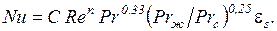(134)

Для шахматных пучков С=0,41; n=0,6; для коридорных пучков С=0,26, n=0,65. Поправочный коэффициент ε_S учитывает влияние относительных

шагов; для шахматного пучка при 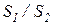< 2, ε_S =(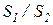)^1/6; при 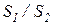≥2, ε_S=1,12; для коридорного пучка ε_S =( 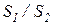)^-0,15. Формула (134) действительна при Re =10³ – 10⁵. В качестве определяющего линейного размера принят внешний диаметр труб; в качестве определяющей температуры – средняя

температура жидкости; скорость определяется в самом узком сечении пучка труб.

Среднее значение коэффициента теплоотдачи для всего пучка, состоящего из n рядов, определяется по формуле:

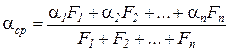(135)

где F₁ , F₂,…, F_n – поверхности теплообмена в соответствующем ряду.

Если предположить, что в ряду F₁ = F₂= F₃,…, F_n и учитывая, что α₃=α₄= …=α_n, то можно написать

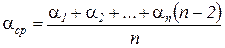(136)

Принимая во внимание приближенные значения α₁ и α₂, получим:

для коридорного пучка

; (137)

для шахматного пучка

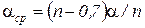(138)

Date: 2015-05-09; view: 1477; Нарушение авторских прав