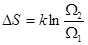Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Энтропия и вероятность. Если макросистема находится в неравновесном состоянии, то она самопроизвольно будет переходить в состояние с большей вероятностью – равновесное
|
|
Если макросистема находится в неравновесном состоянии, то она самопроизвольно будет переходить в состояние с большей вероятностью – равновесное.
Вместе с тем, все самопроизвольные процессы согласно второго закона в замкнутых макросистемах сопровождаются возрастанием энтропии. Поэтому, между S макросистемы в каждом состоянии и вероятностью того же состояния должна существовать определенная связь. Эта связь была найдена Больцманом: 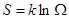
Рассмотрим для примера самопроизвольный изотермический процесс расширения газа в вакуум от V1 до V2 , (A=0) 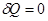 ,
, 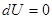 , рис.. Вначале газ находится в объеме V1, он отделен легкой перегородкой, затем ее мгновенно убирают, газ расширяется, но работы не совершает, т.к. ничто ему не препятствует, A=0, Q=0;
, рис.. Вначале газ находится в объеме V1, он отделен легкой перегородкой, затем ее мгновенно убирают, газ расширяется, но работы не совершает, т.к. ничто ему не препятствует, A=0, Q=0; 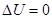 , поскольку, T=const.
, поскольку, T=const.
 |
0 V1 V2 V0
Рис.
Найдем вероятности размещения молекул газа в объемах 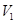 и
и 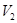 .
.
Вероятность одной молекулы находиться в объеме 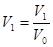
Вероятность всех N молекул находиться в объеме 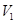 равна
равна 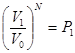 , как вероятность независимых событий.
, как вероятность независимых событий.
Вероятность всех N молекул находиться в объеме 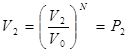 отсюда отношение этих вероятностей:
отсюда отношение этих вероятностей: 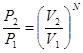 (*)
(*)
Приращение энтропии здесь считают по обратимому изотермическому процессу.
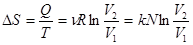 , т.к.
, т.к. 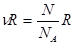
Тогда, подставляя сюда отношение объемов из уравнения (*), получим:
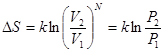
|
 ~
~  , то
, то
Т.е., следует знаменитая формула Больцмана: 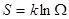 .
.
Принцип возрастания энтропии со статистической точки зрения привел Больцмана к фундаментальному выводу: все макросистемы стремятся переходить от состояний менее вероятных к состояниям более вероятным. При этом сама энтропия характеризует степень беспорядка в макросистеме: состояниям с большей S соответствует больший беспорядок.
С этим связана и необратимость реальных самопроизвольных тепловых процессов: они протекают так, что беспорядок в макросистеме растет. С этим связано и то, что любой вид энергии в итоге переходит во внутреннюю, т. е., в состояние при котором «хаос» максимален. Это состояние называется равновесным, его энтропия S=max, распределение молекул по скоростям будет максвелловским.
[D1]Степень е –
(-m(vz)2)/2kT
[D2]Степень е –
(-m(vz)2)/2kT
[D3]Степень е –
(-m(vx)2)/2kT
[D4]Степень е –
(-m(vy)2)/2kT
[D5]Степень е –
(-mv2)/2kT
[D6]Степень е –
(-mv2)/2kT
[D7]Степень е –
(-mv2)/2kT
[D8]Степень е –
(-mv2)/2kT
[D9]Степень е –
(-mv2)/2kT
[D10]Степень е –
(-mv2)/2kT
[D11]Степень е –
(-mv2)/2kT
[D12]Степень е –
(-mv2)/2kT
[D13]Степень е –
(-mv2)/2kT
[D14]Степень е –
(-mv2)/2kT
[D15]Степень е –
(-mv2)/2kT
[D16]Степень е –
(-mv2)/2kT
Date: 2015-05-09; view: 844; Нарушение авторских прав