Свойства обратимых и необратимых циклов. I и II интегралы Клаузиуса

Одним из важнейших понятий термодинамики является понятие об обратимых и необратимых процессах.

Термодинамический процесс представляет собой совокупность непрерывно изменяющихся состояний термодинамической системы. Между двумя состояниями 1 я 2 системы можно представить себе два процесса, проходящих по одному и тому же пути: от состояния / к состоянию 2 и, наоборот, от состояния 2 к состоянию 1, так называемые прямой и обратный процессы.

Обратимыми называют процессы, в результате совершения которых в прямом и обратном направлениях термодинамическая система возвращается в исходное состояние; таким образом, совокупность прямого и обратного процессов не вызывает в окружающей среде никаких изменений.

Например, при рассмотрении двух плоскостей Л и В, на одной из которых в точке 1 помещен шарик (рис. 3.3), видим, что при своем движении вниз шарик приобретает кинетическую энергию за счет убыли потенциальной энергии. В точке 3 шарик обладает определенной кинетической энергией, за счет которой он поднимается на другую плоскость; его кинетическая энергия убывает, но за счет этого возрастает потенциальная энергия. Если трение между шариком и поверхностью, по которой он перемещается, отсутствует и отсутствует также сопротивление воздуха движению шарика, то в соответствии с законами механики при движении по плоскости шарик поднимается на ту же высоту, с которой он начал свое движение по плоскости Л, т. е. точки 1 и 2 располагаются на одной и той же высоте над горизонтом г. В точке 2 подъем шарика прекратится, его скорость станет равной нулю и он будет спускаться вниз, поднимаясь затем по поверхности А в точку / и т. д.

При оговоренных нами условиях (отсутствие трения о поверхность и сопротивления воздуха) рассмотренный процесс обратим — он совершенно одинаково идет и в направлении 1-3-2, и в противоположном (обратном) направлении 2-3-1; ии одно из этих двух направлений не является для рассматриваемого процесса сколько-нибудь предпочтительным.

Можно (и это видно, в частности, из приведенного примера) определить понятие обратимого процесса следующим образом-, обратимый процесс — это такой процесс, который можно провести в обратном направлении, затрачивая работу, произведенную в прямом процессе.

В случае обратимых процессов обратный процесс представляет собой, так сказать, «зеркальное отображение» прямого процесса; если, например, в прямом процессе к системе подводится какое-то количество теплоты, то в обратном процессе от системы отводится точно такое же количество теплоты (и при той же температуре, при которой подводилось в прямом); если в прямом процессе система совершает работу над внешней средой, то в обратном процессе внешняя среда производит над системой работу, равную по абсолютной величине работе в прямом процессе; если в прямом процессе система расширяется, то в обратном процессе имеет место сжатие системы и т. д.

Необратимыми называют процессы, при проведении которых в прямом и затем в обратном направлении система не возвращается в исходное состояние (т. е. в ходе процесса в системе происходят изменения, которые отличают ее состояние после проведения обратного процесса от состояния, в котором она находилась до проведения прямого процесса). Из повседневной практики известно, что все естественные самопроизвольные процессы, происходящие в природе, являются необратимыми; обратимых процессов в природе не существует.

Рассмотрим обратимый процесс по пути 1а2 и 2б1. Т.к. процессе 1а2б1 обратимый, то для него справедливо равенство Клаузиуса

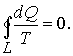
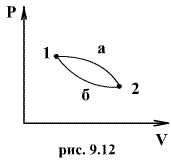
Разобьем этот интеграл на два: по пути 1а2 и 2б1

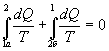
Поменяем пределы интегрирования второго интеграла

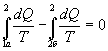
или

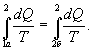
Таким образом, сумма приведенных теплот при переходе из одного состояния в другое не зависит от формы (пути) перехода в случае обратимых процессов. Последнее утверждение носит название теоремы Клаузиуса.