Техническая термодинамика. основные понятия и исходные положения

основные понятия и исходные положения

ПРЕДМЕТ И МЕТОДЫ ТЕРМОДИНАМИКИ

Термодинамика изучает законы превращения энергии в различных процессах, происходящих в макроскопи­ческих системах и сопровождающихся тепловыми эффектами. Макроскопиче­ской системой называется любой матери­альный объект, состоящий из большого числа частиц. Размеры макроскопиче­ских систем несоизмеримо больше разме­ров молекул и атомов.

В зависимости от задач термодинамику разделяют на техническую или химиче­скую термодинамику, термодинамику биологических систем и т, д. Техническая термодинамика изучает закономерности взаимного превращения тепловой и механической энергии и свойства тел, участвующих в этих превраще­ниях. Вместе с теорией теплообмена она является теоретическим фундаментом теплотехники. На ее основе осуществля­ют расчет и проектирование тепло­вых двигателей.

Физические свойства макроскопиче­ских систем изучаются статистическим и термодинамическим методами. Статистический метод основан на использовании теории вероятностей и определенных моделей строения этих систем и пред­ставляет собой содержание статистиче­ской физики. Термодинамический метод не требует привлечения модельных пред­ставлений о структуре вещества и явля­ется феноменологическим (т. е. рассматривает «феномены» — яв­ления в целом). При этом все основные выводы термодинамики можно получить методом дедукции, используя только два основных эмпирических закона (начала) термодинамики,

ТЕРМОДИНАМИЧЕСКАЯ СИСТЕМА

Термодинамическая система представляет собой совокуп­ность материальных тел, находящихся в механическом и тепловом взаимодей­ствиях друг с другом и с окружающими систему внешними телами (внешней средой).

Тела, не входящие в систему, называют окру­жающей средой. Систему отделя­ют от окружающей среды контроль­ной поверхностью (оболочкой). Так, например, для газа, заключенного в цилиндре над поршнем, внешней средой является окру­жающий воздух, а контрольными повер­хностями служат стенки цилиндра, головки и по­ршня.

При механическом взаимодейст­вии самой системой или над системой совершается работа. В двигателях внутреннего сгорания ме­ханическая работа производится при пе­ремещении поршня и сопровождается изменением объема. Тепловое взаимо­действие заключается в переходе тепло­ты между отдельными телами системы и между системой и окружающей средой.

Система мо­жет обмениваться со средой и веществом (массообменное взаимодействие). Такая система называется открытой. Пото­ки газа во впускных и в выпускных трубопро­водах - примеры открытых систем. Если вещество не проходит через границы системы, то она называется закры­той.

Термодинамическую систему, кото­рая не может обмениваться теплотой с окружающей средой, называют теп­лоизолированной или адиа­батной. Примером адиабатной систе­мы является газ, находящийся в сосуде, стенки которого покрыты идеальной теп­ловой изоляцией, исключающей теплооб­мен между заключенным в сосуде газом и окружающими телами. Такую изоляци­онную оболочку называют адиабатной. Система, не обменивающаяся с внешней средой ни энергией, ни ве­ществом, называется изолирован­ной (или замкнутой).

Простейшей термодинамической системой является рабочее тело, осуществляющее взаимное превращение теплоты и работы. В двигателе внутрен­него сгорания, например, рабочим телом является приготовленная в системе смесеобразования горючая смесь, состоящая из воздуха и паров бензина.

ТЕРМОДИНАМИЧЕСКИЕ ПАРАМЕТРЫ СОСТОЯНИЯ

К термодинамиче­ским параметрам относятся давление, абсолютная температура и удельный объем.

Давление обусловлено взаимо­действием молекул рабочего тела с по­верхностью и численно равно силе, дей­ствующей на единицу площади повер­хности тела (р=Р/F). В соответствие с молекулярно-кинетической теорией давление газа определяется соотношением:

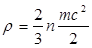, (1.1)

где n – число молекул в единице объема;

m – масса молекулы;

c² – средняя квадратичная скорость поступательного движения молекул.

В Международной системе единиц (СИ) давление выражается в паскалях (1 Па = 1 Н/м²). Поскольку зга едини­ца мала, удобнее использовать 1 кПа = 1000 Па и 1 МПа = 10⁶ Па,

Давление измеряется при помощи манометров, барометров и вакуумметров. Манометры измеряют избыточное давление, пред­ставляющее собой разность между пол­ным или абсолютным давлением р изме­ряемой среды и атмосферным давлением р_атм, т. е. p_изб = р – р_атм.

Приборы для измерения давлений ниже атмосферного называются вакуум­метрами; их показания дают значение разрежения (или вакуума): р_в= р_атм – р, т.е. избыток атмосферного давления над абсолютным.

Следует отметить, что параметром состояния является абсолютное давление. Именно оно входит в термодинами­ческие уравнения.

Температурой называется фи­зическая величина, характеризующая степень нагревания тела. Понятие о температуре вытекает из следующего утвер­ждения: если две системы находятся в тепловом контакте, то в случае нера­венства их температур они будут обмениваться теплотой друг с другом, если же их температуры равны, то теплообмена не будет.

Температура есть мера интенсивности теплового движения молекул (молекулярно-кинетическая теория). Ее численное значение связано с величиной средней кинетической энер­гии молекул вещества:

(1.2)

где k — постоянна Больцмана, равная 1,380662·10^-23 Дж/К. Температура Т. определенная таким образом, называет­ся абсолютной.

В системе СИ единицей температуры является кельвин (К), на практике широ­ко применяется градус Цельсия (°С). Со­отношение между абсолютной температурой Т и стогра­дусной t температурой имеет вид:

Т = t +273,15 ≈ t +273.

В промышленных и лабораторных ус­ловиях температуру измеряют с по­мощью жидкостных термометров, пиро­метров, термопар и других приборов.

Удельный объем v — это объем единицы массы вещества. Если однородное тело массой М занимает объем V. то по определению v = V/M.

В системе СИ единица удельного объема 1 м³/кг. Между удельным объемом v вещества и его плотностью ρ (ρ = М / V) существует очевидное соотношение:

v =1/ ρ или v · ρ = 1.

Нормальные физи­ческие условия. Для сравнения величин, характери­зующих системы в одинаковых состояни­ях, вводится понятие нормальные физи­ческие условия:

Р = 760 мм рт. ст. = 101,325 кПа; Т = 273,15 К или t = 0⁰С.

В разных отраслях техники и разных странах вводят свои, несколько отличные от приведенных «нормальных условий», например, «технические»: (р = 735,6 мм.рт.ст. = 98 кПа; t = 15⁰С). Обычно, если это не оговорено особо, используют нормальные физи­ческие условия.

Если все термодинамические пара­метры постоянны во времени и одинако­вы во всех точках системы, то такое состояние системы называется равновесным.

Если между различными точками в системе существуют разности (градиенты) температур, давлений и других параметров, то она является неравновесной. В такой системе под действием гради­ентов параметров возникают потоки теп­лоты, вещества и другие, стремящиеся вернуть ее в состояние равновесия. Опыт показывает, что изолированная система с течением времени всегда приходит в со­стояние равновесия и никогда самопро­извольно выйти из него не может. В классической термодинамике рассмат­риваются только равновесные системы.

УРАВНЕНИЕ СОСТОЯНИЯ

Для равновесной термодинамической системы существует функциональная связь между параметрами состояния, которая называется уравнением состояния. Опыт показывает, что удель­ный объем, температура и давление про­стейших систем, которыми являются газы, пары или жидкости, связаны термическим уравнением состо­яния вида: f (р, v,Т) = 0.

Уравнению состояний можно придать другую форму: р = f₁ (v,Т); v = f₂ (р,Т); Т = f₃ (v, р). Эти уравнения показывают, что из трех основных параметров, определяю­щих состояние системы, независимыми являются два любых.

Для решения задач методами термо­динамики совершенно необходимо звать уравнение состояния. Однако, оно не мо­жет быть получено в рамках термодина­мики и должно быть найдено либо экспе­риментально, либо методами статистиче­ской физики. Конкретный вид уравнений состояния зависит от индивидуальных свойств вещества.

Уравнение состояния идеальных га­зов. Из уравнений (1.1) и (1.2) следует, что ρ = nkT. Рассмотрим 1 кг газа. Учитывая, что в нем содержится N молекул и, следова­тельно, n =N/v, получим: pv/T = Nk = const.

Постоянную величину Nk, отнесен­ную к 1 кг газа, обозначают буквой R (дж/кг·град) и называют газовой постоян­ной. Поэтому:

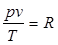, или pv = RT. (1.3)

По определению - газовая постоянная есть работа, которую совершает 1 кг идеального газа в процессе р = const при изменении его температуры на 1 градус.Соотношение (1.3) представляет собой уравнение Клапейрона (1834 г.).

Умножив (1.3) на M, получим уравнение состояния для произвольной массы газа M:

pV = M RT (1.4)

Уравнению Клапейрона можно при­дать универсальную форму, если отнести газовую постоянную к 1 киломолю газа, т.е. к количеству газа, масса которого в килограммах численно равна молеку­лярной массе μ. Положив в (1.4) М = μ и V = V_μ получим для одного моля урав­нение Клапейрона — Менделеева:

рV_μ = μRT. (1.5)

Здесь V_μ — объем киломоля газа, а μR - универсальная газовая постоянная,

В соответствии с законом Авогадро (1811 г.) объем 1 киломоля, одинаковый в одних и тех же условиях для всех иде­альных газов, при нормальных физических условиях равен 22.4 м³, поэтому:

μR = рV_μ / Т = 101,325·22.4/273,15 = 8314 Дж/ (кмоль·К).

Газовая постоянная 1 кг газа составляет:

R = 8314/ μ (1.6)

Уравнение состояния реальных газов. В реальных газах в отличие от иде­альных существенны силы межмолекулярных взаимодействий (силы притяжения, когда молекулы находятся на значительном расстоянии, и силы отталкивания при достаточном сближении их друг с другом), и поэтому нельзя пренебречь собствен­ным объемом молекул.

Наличие межмолекулярных сил отталкивания приводят к тому, что молеку­лы могут сближаться между собой толь­ко до некоторого минимального расстоя­ния. Поэтому можно считать, что свобод­ный для движения молекул объем будет равен v - b, где b - тот наименьший объем, до которого можно сжать газ. В соответствии с этим длина свободного пробега молекул уменьшается и число ударов о стенку в единицу времени, а, следовательно, и давление увеличива­ется по сравнению с идеальным газом.

Силы притяжения действуют в том же направления, что и внешнее давление, и приводят к возникновению молеку­лярного (или внутреннего) давления. Сила молекулярного притяжения каких-либо двух малых частей газа пропорцио­нальна произведению числа молекул в каждой из этих частей, т. е. квадрату плотности, поэтому молекулярное давле­ние p_мол обратно пропорционально квадрату удельного объема газа: p_мол = a/v², где а — коэффициент пропорциональности, зависящий от природы газа.

Отсюда получаем уравнение Ван-дер-Ваальса (1873 г.):

.

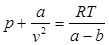При больших удельных объемах и сравнительно невысоких давлениях ре­ального газа уравнение Ван-дер-Ваальса практически вырождается в уравнение состояния идеального газа Клапейрона, ибо величина а/v² (но сравнению с р) и b (no сравнению с v) становятся прене­брежимо малыми.

Уравнение Ван-дер-Ваальса с ка­чественной стороны достаточно хорошо описывает свойства реального газа, но результаты численных расчетов не всег­да согласуются с экспериментальными данными.

ОБРАТИМЫЕ И НЕОБРАИМЫЕ ПРОЦЕССЫ

Пусть в результате некоторого процесса в изолированной системе тело переходит из состояния А в состояние В и затем возвращается в начальное состояние А. Процесс называется обратимым, если возможно осуществить обратный переход из В в А через те же промежуточные состояния так, чтобы не осталось никаких изменений в окружающих телах. Если такой обратный переход осуществить нельзя, если по окончании процесса в окружающих телах или в самом теле остались какие-то изменения, то процесс является необратимым.

Любой процесс, сопровождаемый трением, является необратимым, ибо при трении часть работы всегда превращается в тепло.

Все процесс, сопровождающиеся теплопередачей от нагретого тела к менее нагретому, являются необратимыми.

Необратимыми являются процессы расширения газа, даже идеального, в пустоту.

Все реальные процессы являются необратимыми, хотя степень необратимости может быть весьма различной.

РАВНОВЕСНЫЕ И НЕРАВНОВЕСНЫЕ ПРОЦЕССЫ

Термодинамическое равновесие- это такое состояние изолированной системы, при котором все термодинамические параметры остаются неизменными в течение сколь угодно долгого времени.

Равновесным процессом называют процесс, состоящий из ряда следующих друг за другом равновесных состояний. Параметры двух таких состояний отличаются на бесконечно малую величину. Равновесный процесс может быть только бесконечно медленным процессом.

При равновесном процессе, который может протекать и в неизолированной системе, внешнее давление (или температура) взаимодействующего тела отличается от давления (или температуры) тела на бесконечно малую величину.

ПЕрвый закон термодинамики

Закон сохранения и превращения энергии является фундаментальным законом природы. Энергия не исчезает и не возникает вновь, она лишь переходит из одной формы в другую, причем убыль энергии одного вида дает эквивалентное количество энергии другого вида.

Пусть некоторому рабочему телу с объемом V и массой М, имеющему температуру Т и давление р, сообщается извне бесконечно малое количеств тепло­ты δQ. В результате подвода теплоты тело нагревается на dT и увеличивается в объеме на dV.

Повышение температуры тела свиде­тельствует об увеличении кинетической энергии его частиц. Увеличение объема тела приводит к изменению потенциаль­ной энергии частиц. В результате внут­ренняя энергия тела увеличивается на dU. Поскольку рабочее тело окружено средой, которая оказывает на него давление, то при расширении оно произво­дит механическую работу δL против сил внешнего давления. Так как никаких других изменений в системе не происхо­дит, то по закону сохранения энергии:

δQ = dU + δА, (2.7)

т.е. теплота, сообщаемая системе, идет на приращение ее внутренней энергии U и на совершение внешней работы L.

Полученное уравнение является ма­тематическим выражением первого зако­на термодинамики. Каждый из трех чле­нов этого соотношения может быть поло­жительным, отрицательным или равным нулю. Рассмотрим некоторые частные случаи.

1) δQ = 0 — теплообмен системы с ок­ружающей средой отсутствует, т.е. теп­лота к системе не подводится и от нее не отводится. Процесс без теплообмена на­зывается адиабатным. Для него уравнение (2,7) принимает вид

δА = - dU. (2.8)

Следовательно, работа расширения, совершаемая системой в адиабатном процессе, равна уменьшению внутренней энергии данной системы, При адиабатном сжатии рабочего тела затрачивае­мая извне работа целиком идет на увели­чение внутренней энергии системы.

2) δА = 0 - при этом объем тела не изменяется, dV = 0. Такой процесс на­зывается изохорным. Для этого процесса:

δQ = dU, (2.9)

т.е. количество теплоты, подведенной к системе при постоянном объеме, равно увеличению внутренней энергии данной системы.

3) dU = 0 – внутренняя энергия системы не изменяется:

δQ = δА, (2.10)

т.е. сообщаемая системе теплота превращается в эквивалентную ей внешнюю работу.

Для системы, содержащей 1 кг рабочего тела:

δq = du + δа. (2.11)

Проинтегрировав уравнение (2.7) и (2.11) для некоторого процесса, получим выражение первого закона термодинамики в интегральной форме:

Q = ΔU + А; q = Δu + а, (2.12)

где ΔU = U₂ – U₁; Δu = u₂ – u₁.

ВНУТРЕННЯЯ ЭНЕРГИЯ

Внутренняя энергия системы включа­ет в себя:

· кинетическую энергию поступательного, вращательного и колебательного движения частиц;

· потенциальную энергию взаимодей­ствия частиц;

· энергию электронных оболочек атомов;

· внутриядерную энергию.

В большинстве теплоэнергетических процессов две последние составляющие остаются неизменными, Поэтому обычно под внутренней энер­гией понимают энергию хаотиче­ского движения молекул и атомов, вклю­чающую энергию поступательного, вра­щательного и колебательного движений как молекулярного, так и внутримолекулярного, а также потенциальную энергию сил взаимодействия между молекулами.

Кинетическая энергия молекул является функцией температуры. Значение потенциальной энергии зависит от сред­него расстояния между молекулами и, следовательно, от занимаемого газом объема V, т. е. является функцией V. Поэтому внутренняя анергия U есть функция состояния тела.

Для сложной системы она определя­ется суммой энергий отдельных частей, т.е. обладает свойством аддитивности. Величина u = U/M, называемая удельной внутренней энер­гией (Дж/кг), представляет собой внутреннюю энергию единицы массы вещества.

В дальнейшем для краткости будем называть величину u просто внутренней энергией. Поскольку внутренняя энергия есть функция состояния тела, то она мо­жет быть представлена в виде функции двух любых независимых параметров, определяющих это состояние:

u = ψ₁ (p,V); u = ψ₂ (p,Т); u = ψ₃ (v,Т).

Ее изменение в термодинамическом процессе Δu не зависит от характера процесса и определяется только началь­ным и конечным состояниями тела:

,

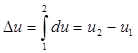где u₁ - значение внут­ренней энергии в начальном состоянии, а u₂ - в конечном.

Математически это означает, что бесконечно малое измене­ние внутренней энергии du есть полный дифференциал u.

Внутренняя энергия идеального газа, в котором отсутствуют силы взаимодей­ствия между молекулами, не зависит от объема газа или давления, a определяется только его температурой, поэтому производная от внутренней энергии идеального газа по температуре есть полная производная:

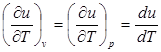. (2.2)

Для задач технической термодинами­ки важно не абсолютное значение внут­ренней энергии, а ее изменение в различ­ных термодинамических процессах. Поэтому начало отсчета внутренней энер­гии может быть выбрано произвольно. В соответствии с международ­ным соглашением для идеальных газов за нуль принимается значение внутренней энергии при температуре 0⁰С вне зависимости от давления.

РАБОТА РАСШИРЕНИЯ

Работа в термодинамике, так же как и в механике, определяется произведени­ем действующей на рабочее тело силы на путь ее действия.

Рассмотрим газ массой М и объемом V, заключенный в эластичную оболочку с поверхностью F (рис. 2.1).

Рис.2.1. К определению работы расширения.

Если газу сообщить некоторое количество теплоты, то он будет расширяться, совершая при этом работу против внешнего давления р, оказываемого на него средой. Газ дей­ствует на каждый элемент оболочки dF с силой, равной pdF и, перемещая ее по нормали к поверхности на расстояние dn, совершает элементарную работу pdFdn. Общую работу, совершенную в течение бесконечно малого процесса, получим, интегрируя данное выражение по всей поверхности F оболочки:

.

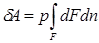Из рис. 2.1 видно, что изменение объема dV выражается в виде интеграла по поверхности:

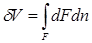, следова­тельно:

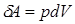(2.3)

При конечном изменении объема работа против сил внешнего давления, называе­мая работой расширения, равна:

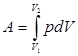(2.4)

Из (2.3) следует, что при расширении работа тела положительна, при этом тело само совершает работу; при сжатии работа тела отрицательна; это означает, что не тело совершает работу, а на его сжатие затрачивается работа извне.

Единицей измерения работы в системе СИ яв­ляется джоуль (Дж).

Отнеся работу расширения к 1 кг массы рабочего тела, получим:

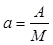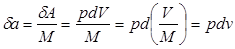; (2.5)

Величина l, представляющая собой удельную работу, совершаемую систе­мой, содержащей 1 кг газа, равна:

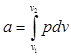(2.6)

Поскольку в общем случае р — величина переменная, то интегрирование воз­можно лишь тогда, когда известен закон изменении давления р = р (v).

Формулы (2.3)…(2.6) справедливы только для равновесных процессов, при которых давление рабочего тела равно давлению окружающей среды.

В термодинамике для исследования равновесных процессов широко исполь­зуют р - v диаграмму, в которой осью аб­сцисс служит удельный объем, а осью ординат - давление. Заметим, что в практике исследования поршневых двигателей используют так называемую индикаторную диаграмму рабочего (реального) цикла, которая получается с помощью специального устройства (системы), называемого индикатором (системой индицирования).

Поскольку состоя­ние термодинамической системы опреде­ляется двумя параметрами, то на р - v -ди­аграмме оно изображается точкой. На рис. 2.2 точка 1 соответствует начально­му состоянию системы, точка 2 — конеч­ному, а линия 1-2 - процессу расшире­ния рабочего тела от v₁ до v₂.

При бесконечно малом изменении объема dv площадь заштрихованной вертикальной полоски раина pdv = δа.

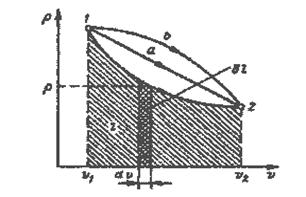
Рис.2.2. Графическое изображение работы в р- v - координатах.

Следовательно, работа процесса 1-2 изо­бражается площадью, ограниченной кривой процесса, осью абсцисс и крайними ординатами. Таким образом, робота из­менения объема эквивалентна площади под кривой процесса в диаграмме р- v.

Каждому пути перехода системы из состояния 1 в состояние 2 (например, 1-а-2 или 1-b-2) соответствует своя работа расширения:

аl_1-b-2 > а_1-а-2 .

Следовательно, работа зависит от характера термодинамического процесса, а не явля­ется функцией только исходного и конечного состояний системы. С другой стороны, ∫pdv зависит от пути интегри­рования и, следовательно, элементарная работа δа не является полным диффе­ренциалом.

Работа всегда связана с перемеще­нием макроскопических тел в простран­стве, например, перемещением поршня двигателя, поэтому она характеризует упорядоченную (макрофизическую) форму передачи энергии от од­ного тела к другому и является мерой переданной энергии.

Поскольку величина δа пропорцио­нальна увеличению объема, то в качестве рабочих тел, предназначенных для пре­образования тепловой энергии в механи­ческую работу, целесообразно выбирать такие, которые обладают способностью значи­тельно увеличивать свой объем. Этим качеством обладают газы и пары жидкостей. Поэтому, например, на тепловых электрических станциях рабочим телом служат пары воды, а в двигателях внут­реннего сгорания — газообразные про­дукты сгорании топлива.

ТЕПЛОТА

Помимо макрофизической формы передачи энергии - работы существует также и микрофизическая форма, т.е. осуще­ствляемая на молекулярном уровне фор­ма обмена энергией между системой и окружающей средой. В этом случае энергия может быть передана системе без совершения работы. Мерой количест­ва энергии, переданной микрофизическим путем, служит теплота.

Теплота может передаваться либо при непосредственном контакте между телами (теплопроводностью, конвек­цией), либо на расстоянии (излучением), причем во всех случаях этот процесс возможен только при наличии разности (градиента) температур между телами.

Как будет показано ниже, элементар­ное количество теплоты δQ, так же как и δА, не является полным дифференциа­лом в отличие от дифференциала внут­ренней энергии dU. За этой математиче­ской символикой скрыт глубокий физиче­ский смысл различия понятий внутрен­ней энергии, теплоты и работы.

Внутренняя энергия – это свойство самой системы, она характеризует состо­яние системы. Теплота и работа — это энергетические характеристики процес­сов механического и теплового взаи­модействий системы с окружающей средой. Они характеризуют те количест­ва энергии, которые переданы системе или отданы ею через ее границы в опре­деленном процессе.

теплоемкость газов

Отношение количества теплоты δQ, полученного телом при бесконечно малом изменении его состояния, к изменению температуры тела dТ называется теплоемкостью тела в данном процессе:

.

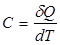Обычно теплоемкость относят к единице количества вещества и в зависимости от выбранной единицы различают:

- удельную массовую теплоемкость c, отнесенную к 1 кг газа, Дж /(кг·К);

- удельную объемную теплоемкость c ׳, отнесенную к количеству газа, содержащегося в 1 м³ объема при нормальных физических условиях, Дж /(м³·К);

- удельную мольную теплоемкость μc, отнесенную к одному киломолю, Дж /(кмоль·К).

Взаимосвязь между удельными теплоемкостями устанавливается очевидным соотношениями:

с = μc / μ; c ׳ = сρ_н. (2.13)

Здесь ρ_н - плотность газа при нормальных условиях.

Изменение температуры газа при одном и том же количестве сообщаемой теплоты зависит от характера происходящего при этом процесса. Поэтому теплоемкость является функцией процесса. Это означает, что одно и то же рабочее тело в зависимости от процесса требует для своего нагревания на 1К различного количества теплоты.

В термодинамических расчетах большое значение имеют:

- теплоемкость при постоянном давлении (изобарная теплоемкость):

с_р = δq_р / dТ, (2.14)

равная отношению количества теплоты δq_р, сообщенной телу в процессе при постоянном давлении, к изменению температуры тела dТ;

- т еплоемкость при постоянном объеме (изохорная теплоемкость):

с_v = δq_v / dТ, (2.15)

равная отношению количества теплоты δq_v, подведенной к телу в процессе при постоянном объеме, к изменению температуры тела dТ. Теплоемкость тела при постоянном объеме равна производной от его внутренней энергии по температуре и характеризует темп роста внутренней энергии в изохорном процессе с увеличением температуры. То есть для идеального газа имеем: с_v = du / dТ, (2.18)

Существует связь между теплоемкостями с_р и с_v. Для иде­ального газа она имеет вид:

с_р = с_v + R. (2.20)

Соотношение (2.20) называется уравнением Майера, которое является одним из основных в технической термодинамике идеальных газов.

В изохорном процессе (v =const) теплота сооб­щаемая газу, идет лишь на изменение его внутренней энергии, тогда как в изобарном процессе (р = const) теплота расходуется и на увеличение внутренней энергии и на совершение работы против внешних сил. Поэтому с_р больше с_v на величину этой работы.

Обычно теплоемкости определяются экспериментально, но для многих ве­ществ их можно рассчитать методами статистической физики.

Молекула одноатомного газа имеет три степени свободы соответственно по трем состав­ляющим в направлении координатных осей, на которые может быть разлажено поступатель­ное движение. Молекула двухатомного газа имеет пять степеней свободы, так как помимо поступательного движения она может вращаться около двух осей, перпендикулярных линии, соединяющей атомы. Молекула трехатомного и вообще многоатомного газа имеет шесть степеней свободы, три поступательных и три вращательных.

С учетом классической теоремы о равномерном распределении энергии по степеням свободы, мольные теплоемкости μc одно-, двух- и многоатомных идеальных газов равны соответственно: 12,5; 20,8 и 24,9 кДж /(кмоль·К).

Результаты классической теории теплоемкости достаточно хорошо согласуются с экспериментальными данными в области комнатных температур, однако основной вы­вод о независимости от температуры экспериментом не подтверждается. Расхождения, особенно существенные в области низких и достаточно высоких температур, связаны с квантовым по­ведением молекул и находят объяснения в рамках квантовой теории теплоемкости.

Теплоемкость реального газа зависит от давления очень слабо.

Поскольку теплоемкость газа зависит от температуры, в термоди­намике различают истинную и среднюю теплоемкости.

Средней теплоемкостью с_ср данного процесса в интер­вале температур от t₁ до t₂ называется отношение количества тепло­ты, сообщаемой газу, к разности конеч­ной и начальной температур:

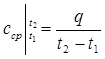(2.21)

Выражение

(2.22)

определяет теплоемкость при данной температуре или так называемую истинную теплоемкость.

Принцип определения сред­ней теплоемкости с использованием зависимости истинной теплоемкости от температуры показан на рис.2.3.

Для практических расчетов теплоем­кости всех веществ сводят в таблицы, причем с целью сокращения объема таб­лиц средние теплоемкости приводят в них для интервала температур от 0 до t.

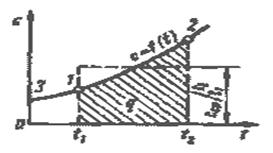
Рис.2.3. Зависимость истинной теплоемкости от температуры.

ЭНТАЛЬПИЯ

В термодинамике важную роль играет сумма внутренней анергии системы U и произведения давления системы р на ее объем V, называемая энтальпией и обозначаемая Н:

H = U + pV. (2.25)

Так как входящие неё величины являются функциями состояния, то и сама энтальпия является функцией (характеристикой) состояния рабочего тела. Так же как внутренняя энергия, работа и теплота, она измеряется в джоулях (Дж).

Энтальпия обладает свойством адди­тивности. Величина

h = u + pv (2,26)

называемая удельной энтальпией (h = Н/М), представляет собой энтальпию системы, содержащей 1 кг ве­щества, и измеряется в Дж/кг.

Поскольку энтальпия есть функция состояния, то она может быть представ­лена в виде функции двух любых пара­метров состояния: р, v, Т. Величина dh является полным диффе­ренциалом.

Изменение энтальпии в любом процессе определяется только начальным и конечным состояниями тела и не зависит or характера процесса. Понятие энтальпии введено в термодинамике на основе чисто формальных соображений, но можно установить и физический смысл этой величины.

Физический смысл энтальпии выяс­ним на следующем примере. Рассмотрим расширенную систему, включающую газ в цилиндре и поршень с грузом общим весом G (рис 2.4). Энергия этой системы складывается из внутренней энергии га­за и потенциальной энергии поршня с грузом в поле внешних сил: Е = U + pV. В условиях равновесия (G = р·F×y) эту функцию можно выразить через па­раметры газа:

Е = р·F×y = U + pV.

Получаем, что Е = Н, т.е. энтальпию можно трактовать как энергию расши­ренной системы.

В случае, когда единственным видом ра­боты является работа расширения, с уче­том очевидного соотношения pdv = d (pv) - v dp можно записать:

δq = d(u + pv) - vdp, или

δq = dh - v dp. (2.27)

Из этого соотношения следует, что если давление системы сохраняется неизменным, т.е. осуществляется изобар­ный процесс (dp = 0), то

δq_р = dh. (2.28)

Рис.2.4. К определению физического смысла энтальпии.

Следовательно:

q_р = h₂ – h₁. (2.29)

Таким образом, теплота, подведенная к системе при постоянном давлении, идет только на из­менение энтальпии данной системы.

Это выражение очень часто исполь­зуется в расчетах, так как огромное ко­личество процессов подвода теплоты в теплоэнергетике (в тепловых двигателях, теплообменных ап­паратах и др.) осуществляется при постоянном давле­нии. Кстати, по этой причине в таблицах термодинамических свойств обычно при­водятся значения энтальпии, а не внут­ренней энергии.

Для идеального газа с учетом того, что d(pv)= R dТ, имеем:

dh = du + d(pv)= с_v dТ + R dТ = (с_v + R) dТ = с_р dТ. (2.30)

Так как между энтальпией к внутрен­ней энергией существует связь (2.26), выбор начала отсчета одной из них не произволен: в точке, принятой за начало отсчета внутренней энергии, h = pv. На­пример, для воды при t = 0,01 °С и р = 610,8 Па, u = 0. а h = рv = 610,8×0,001 = 0,611 Дж/кг.

При расчетах практический интерес представляет изменение энтальпии в ко­нечном процессе:

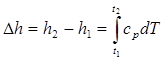(2.31)

Функции состояния и функции процессов. Все наиболее важные термодинамические величины можно разделить на две группы.

К первой группе следует отнести:

1) давление р, н/м² или Па;

2) удельный объем v (характеристика плотности рабочего тела), м³/кг;

3) температура Т или t, К или ⁰С;

4) внутренняя энергия u, Дж/кг;

5) энтальпия h, Дж/кг.

Ко второй группе:

1) теплота (удельная теплота) Q (q), Дж (Дж/кг);

2) работа газа (удельная работа газа), А (а), Дж (Дж/кг).

Для параметров первой группы общим свойством является то, что они определяются только состоянием рабочего тела и не зависят от того, каким образом (в результате какого процесса), тело пришло в данное состояние. На этом основании величины этой группы принято называть функциями состояния. На координатной плоскости (например, р-v) каждому состоянию соответствует некоторая вполне определенная точка.

Вторая группа величин не определяет состояние рабочего тела, а характеризует процесс. Так как работа и теплота представляют собой две возможные формы передачи энергии от одного тела к другому, и их значение зависит от характера процесса, происходящего с этим телом, то их называют функциями процесса.

Контрольные задачи.

1. 1 л воды нагревается с помощью электрического кипятильника мощностью 300 Вт. За какое время вода нагреется до температуры кипения, если теплообмен с окружающей средой отсутствует, а начальная тем­пература воды равна 20⁰С.

2. Найти среднюю удельную теплоем­кость азота винтервале температур 1000…2000⁰.

ВТОРОЙ ЗАКОН ТЕРМОДИНАМИКИ

ЭНТРОПИЯ

Как уже указывалось, величина δq = du+ pdv не является полным дифференциалом. Действительно, для того что­бы проинтегрировать правую часть этого выражения, нужно знать зависимость р от v, т.е. процесс, который соверша­ет газ.

В математике доказывается, что диф­ференциальный двучлен всегда можно превратить в полный дифференциал пу­тем умножения (или деления) на интег­рирующий множитель (или делитель), Таким интегрирующим делителем для элементарного количества теплоты δq является абсолютная температура Т.

Покажем это на примере изменения параметров идеального газа в равновес­ных процессах:

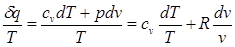(3.1)

Выражение δq/Т при равновесном изменении состояния газа есть полный дифференциал некоторой функции состо­яния. Она называется энтропией, обозначается для 1 кг газа через s и из­меряется в Дж /(кг·К) Для произволь­ного количества газа энтропия, обозна­чаемая через S, равна S = Ms и измеря­ется в Дж/К. Таким образом, аналитически энтро­пия определяется следующим образом;

ds = δq/Т, (3.2)

Формула (3,2) справедлива как для идеальных газов, так и для реальных тел.

Подобно любой другой функции со­стояния энтропия может быть представлена в виде функции любых двух пара­метров состояния:

s = f₁ (р, v); s = f₂ (р, Т); s = f₃ (v,Т).

Значение энтропии для заданного со­стояния определяется интегрированием уравнения (3.2):

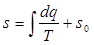
где s₀ — константа интегрирования.

При температурах, близких к абсо­лютному нулю, все известные вещества находятся в конденсированном состоянии. В. Нернст (1906 г.) эксперименталь­но установил, а М Планк (1912 г.) окон­чательно сформулировал следующий принцип: при температуре, стремящейся к абсолютному нулю, энтропия вещества, находящегося в конденсированном состоянии с упорядоченной кристалличе­ской структурой, стремится к нулю, т.е s₀ = 0 при Т =0 К. Этот закон на­зывают третьим законом термодинамики или тепловой теоремой Нернста. Он позволяет рассчитать абсолютное значение энтропии в отличие от внутренней энергии и энтальпии, которые всегда отсчитываются от про­извольного уровня.

Однако в технической термодинамике обычно используется не абсолютное зна­чение энтропии, а ее изменение в каком-либо процессе:

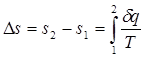(3.3)

Поэтому энтропию тоже часто отсчитыва­ют от произвольно выбранного уровня. Получим формулы, позволяющие вы­числить изменение энтропия идеального газа, Для этого проинтегрируем уравне­ние (3.1), положив для простоты c_v = const:

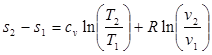(3.4)

Из уравнения Клапейрона, записанного дли состояний 1 н 2, следует:

.

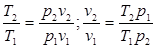После подстановки отношений Т₂/Т₁ и v₂/v₁ в выражение (3.4) получим следующие формулы для изменения энтро­пии идеального газа:

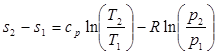(3.5)

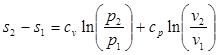(3.6)

Поскольку энтропия есть функция состояния рабочего тела, уравнениями (3.4)…(3.6) можно пользоваться вне зависимости от пути перехода рабочего тела между состояниями 1 и 2 и, в частности, от того, равновесный этот переход или нет.

Понятие энтропии позволяет ввести чрезвычайно удобную для термодинами­ческих расчетов Т-s - диаграмму, на которой (как и на р-v - диаграмме) состояние термодинамической системы изобража­ется точкой, а равновесный термодина­мический процесс линией (рис.3.1).

Из уравнении (3.2) следует, что в равновесном процессе:

δq = Тds (3.7)

(3.8)

Очевидно, что в Т-s - диаграмме эле­ментарная теплота процесса δq изобра­жается элементарной площадкой с высо­той Т и основанием ds, а площадь, огра­ниченная линией процесса, крайними ординатами и осью абсцисс, эквивалент­на теплоте процесса.

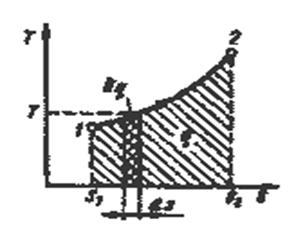
Рис.3.1. Графическое изображение теплоты в Т-s – координатах.

Формула (3.7) показывает, что ds и δq имеют одинаковые знаки, следова­тельно, по характеру изменения энтропии в равновесном процессе можно судить о том, в каком направлении происходит теплообмен. При подводе теплоты к телу (δq > 0) его энтропия возрастает (ds> 0), а при отводе теплоты (δq <0) - убывает (ds <0).

ОБЩАЯ ФОРМУЛИРОВКА ВТОРОГО ЗАКОНА

Из первого закона термодинамики следует, что взаимное превращение теп­ловой и механической энергии в двигате­ле должно осуществляться в строго экви­валентных количествах. Двигатель, который позволял бы получать работу без энергетических затрат, называется веч­ным двигателем первого рода. Ясно, что такой двигатель невозможен, ибо он противоречит первому за­кону термодинамики. Поэтому первый закон можно сформулировать в виде сле­дующего утверждения: вечный двигатель первого рода невозможен. В 1755 г. французская Академия наук «раз и навсегда» объявила, что не будет больше принимать на рассмотрение ка­кие-либо проекты вечных двигателей.

Несмотря на эквивалентность тепло­ты и работы, процессы их взаимного пре­вращения неравнозначны. Опыт показы­вает, что механическая энергия может быть полностью превращена в теплоту, например, путем трения, однако теплоту полностью превратить в механическую энергию в периодически повторяющемся процессе нельзя. Многолетние попытки осуществить такой процесс не увенча­лись успехом, Это связано с существованием фундаментального закона природы, называемого вторым законом термодинамики. Чтобы выяснить его сущность, обратимся к принципиаль­ной схеме теплового двигателя (ряс. 3.2).

Рис.3.2. Термодинамическая схема теплового двигателя.

Как показал опыт, все без исключе­ния тепловые двигатели должны иметь горячий источник теплоты, рабочее тело, совершающее замкнутый процесс - цикл и холодный источник теплоты.

Практически в существующих тепловых двигателях горячими источниками служат химические реакции сжигания топлива, а в качестве холодного источника используется окружающая среда — ат­мосфера. В качестве рабочих тел, как отмечалось выше, применяются газы или пары.

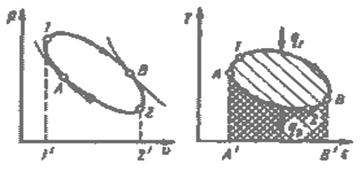
Рис.3.3. Круговой процесс (цикл) в р-v и Т-s – координатах.

Работа двигателя осуществляется следующим образом (рис. 3.3). Расши­ряясь по линии 1-В-2, рабочее тело со­вершает работу, равную площади 1- В-2-2´-1´. В непрерывно действующей тепловой машине этот процесс должен по­вторяться многократно. Для этого нужно уметь возвращать рабочее тело в исходное состояние. Такой переход можно осу­ществить в процессе 2-B-1, но при этом потребуется совершить над рабочим телом ту же самую работу. Ясно, что это не имеет смысла, так как суммарная рабо­та - работа цикла - окажется равной нулю.

Для того чтобы двигатель непрерыв­но производил механическую энергию, работа расширения должна быть больше работы сжатия. Поэтому кривая сжатия 2-A-I должна лежать ниже кривой расширения. Затраченная в процессе 2-А-1 рабо­та изображается площадью 2-А-1-1'-2'. В результате каждый килограмм рабоче­го тела совершает за цикл полезную ра­боту l_ц, эквивалентную площади 1-В-2-А-1, ограниченной контуром цикла. Цикл можно разбить на два участка: А-1-В, на котором происходит подвод теплоты q₁, и В-2-А, на котором происходит отвод теп­лоты q₂. В точках А и В нет ни подвода, ни отвода теплоты, и в этих точках поток теплоты меняет знак. Таким образом, для непрерывной работы двигателя не­обходим циклический процесс, в котором к рабочему телу от горячего источника подводится теплота q₁ и отводится от него к холодному источнику теплота q₂. В Т-s - диаграмме теплота q₁ эквивалентна площа­ди А´-А-1-В-В´, а q₂ — площади А´-А-2-В-В´.

Применим первый закон термодина­мики к циклу, который совершает 1 кг рабочего тела: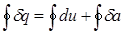

Здесь 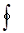означает интегрирование по за­мкнутому контуру 1-B-2-A-1.

Внутренняя энергия системы являет­ся функцией состояния. При возвращении рабочего тела в исходное состояние она также приобретает исходное значение.

Поэтому , и предыдущее вы­ражение превращается в равенство:

q_ц = а_ц (3.9)

где 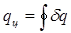представляет собой ту часть теплоты горячего источника, которая превращена в работу. Это — теплота, по­лезно использованная в цикле, она равна разности теплот q₁ - q₂ и эквивалентна площади, ограниченной контуром цикл в Т-s - диаграмме,

Отношены работы, производимой двигателем за цикл, к количеству теплоты, подведенной за этот цикл от горячего источника, называется термическим коэффициентом полезного действия (КПД) цикла:

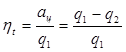(3.10)

Коэффициент полезного действия оценивает степень совершенства цикла теплового двигателя. Чем больше КПД, тем большая часть подведенной теплоты превращается в работу.

Соотношение (3.9) является матема­тическим выражением принципа эквива­лентности тепловой и механической энергии,

Отметим, что если исключить из схемы теплового двигателя холодный источ­ник, то формально принцип эквивален­тности не будет нарушен. Однако, как показывает опыт и как следует из проведенного выше анализа работы двигате­ля, такой двигатель работать не будет.

Тепловой двигатель без холодного источника теплоты, т, е. двигатель, пол­ностью превращающий в работу всю по­лученную от горячего источнике теплоту, называется вечным двигателем второго рода.

Таким образом, второй закон термо­динамики можно сформулировать в виде следующего утверждения: «Вечный дви­гатель второго рода невозможен». В бо­лее расшифрованном виде эту формули­ровку в 1851 г. дал В. Томсон: «Невоз­можна периодически действующая теп­ловая машина, единственным результа­том действия которой было бы получение работы за счет отнятия теплоты от не­которого источника»,

Проблема создания вечного двигателя привлекала исследователей на протяжении длительного времени. Человечество овладело бы неисчерпаемыми запасами внутренней энергии, если бы был построен вечный двигатель второго рода. Действительно, количество теплоты, выделяющейся при охлаждении, например, земного шара всего на 1К [масса земного шара: 6·10²⁴ кг, удельная тепло­емкость: 840 Дж /(кг·К)] равно 5-10²⁷ Дж. Для сравнения следует указать. что а 2000 г, мировое потребление всех энергоресурсов не превышало 5·10²⁰ Дж, т. е. в 10 миллионов раз меньше этой величины.

ЦИКЛ КАРНО

Среди множества исследованных циклов тепловых двигателей именно цикл Карно занимает особое место, выполняя важную научно-методическую роль в общей теории термодинамики. Он служит своеобразным эталоном для оценки совершенства других теплосиловых циклов, преобразующих теплоту в работу. С его помощью определяют максимально возможный КПД этого преобразования в заданном интервале температур.

Рабочий цикл этой идеальной тепловой машины состоит из двух равновесных изотермических и двух равновесных адиабатных процессов. В машине отсутствуют всякие потери на теплопроводность, лучеиспускание, трение и т. д. С машиной связаны два резервуара теплоты. Один, имеющий температуру Т₁, называемы нагревателем, теплоотдатчиком, горячим источником теплоты, другой, имеющий более низкую температуру Т₂- холодильник, теплоприемник, холодный источник теплоты.

В качестве рабочего вещества может быть взято любое упругое тело, хотя обычно рассматривается машина с идеальным газом.

Машина состоит из цилиндра, заполненного рабочим веществом. Поршень цилиндра может перемещаться вертикально, на нем укреплен столик С с песком, который можно сбрасывать на полочки П, мимо которых проходит столик при перемещении поршня.

В цилиндре находится идеальный газ, стенки цилиндра не проводят теплоту, но дно является идеальным проводником теплоты.

Поставим цилиндр на резервуар тепла- теплоотдатчик, имеющий температуру Т₁; начальная температура рабочего вещества в цилиндре также должна равняться Т₁.

Заставим теперь рабочее вещество в цилиндре расширятся изотермически. Для этого будем сбрасывать песок бесконечно малыми порциями на полки, мимо которых перемещается поршень со столиком. При сбрасывании песка такими порциями внешнее давление на поршень уменьшается бесконечно медленно, и процесс расширения будет равновесным. Приток теплоты от теплоотдатчика при таком расширении идет изотермически.

Если на диаграмме состояния начальное состояние газа изображено точкой 1, то процесс изотермического расширения изобразится изотермой 1-2. Когда объем достигает величины V₂ цилиндр снимаем с теплового резервуара и поставим на изолирующую подставку В, не проводящую теплоту. Дальнейшее расширение газа производим адиабатно, продолжая сбрасывать песок на полки. Работа подъема груза теперь совершается за счет внутренней энергии газа, его температура понижается. Когда температура рабочего вещества станет равной температуре Т₂ второго резервуара теплоты- теплоприемника (точка 3 на диаграмме состояния), снимем цилиндр с изолирующей подставки, поместим его на теплоприемник и начнем изотермически сжимать рабочее тело, сбрасывая бесконечно малыми порциями песок с полочек на столик, когда он перемещается мимо них. При этих условиях процесс идет изотермически- теплота, в которую превращается работа сжатия газа, передается теплоприемнику. Когда будет достигнута точка 4, лежащая на одной адиабате с точкой 1, изображающей начальное состояние газа, снимем цилиндр с теплообменника и вновь перенесем его на теплоизолирующую подставку и дальнейшее сжатие производим адиабатно, продолжая сбрасывать песок с полочек на столик. Температура рабочего тела повышается. Процесс прекращаем, когда тело вернется в исходное состояние 1.

Таким образом, осуществлен цикл, состоящий из двух изотермических процессов (расширения и сжатия) и двух адиабатных процессов (тоже расширения и сжатия).

Во время осуществления этого цикла рабочее тело получает от теплоотдатчика количество теплоты Q₁ и отдает теплоприемнику количество теплоты Q₂. За счет разности этих количеств теплоты совершается работа поднятия некоторого количества песка на большую высоту, чем та, на которой он находился в начале цикла. Действительно, при изотермическом расширении давление газа падает медленно, поэтому со столика на полки приходится сбрасывать немного песка. При адиабатном расширении давление падает быстро, поэтому количество сбрасываемого на полки песка должно быть значительно больше. При изотермическом сжатии давление растет медленно, поэтому с верхних полок на столик приходится сбрасывать мало песка; когда же происходит адиабатное сжатие, давление растет быстро, поэтому количество сбрасываемого с нижних полок песка будет значительно больше.

На столике после окончания цикла, очевидно, должно быть столько же песка, сколько его было вначале. Таким образом, работа цикла сводится к тому, что песок перемещается с нижних полок на верхние, т. к. со столика на нижние полки сбрасывается немного песка, а с полок на столик- много. На верхних полках, наоборот, со столика при адиабатном расширении сбрасывается много песка, а при изотермическом сжатии с полок на столик очень много. Для этого на нижних полках должен быть достаточно большой запас песка.

Рассчитаем коэффициент полезного действии идеальной тепловой машины, работающей по циклу Карно:

.

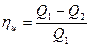Полезная работа А_ц=Q₁-Q₂ равна сумме всех работ, выполненных при осуществлении отдельных частей цикла.

q₁=T₁(s₂-s₁).

q₂=T₂(s₂-s₁).

.

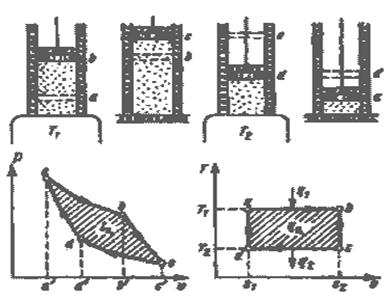
Рис.3.4. Цикл Карно.

Таким образом, в результате цикла каждый килограмм газа получает от го­рячего источника теплоту q₁, отдает хо­лодному теплоту q₂ и совершает работу а_ц.

Подставив в формулу (3.10), спра­ведливую дли любого цикла, выраже­ния для q₁ и q₂, подучим, что терми­ческий КПД цикла Карно определяет­ся формулой:

η_ц = 1 – Т₁/Т₂ (3.11)

Из нее видно, что термический КПД цикла Карно зависит только от абсолют­ных температур горячего и холодного источников. Увеличить КПД цикла мож­но либо за счет увеличения температуры горячего источника, либо за счет умень­шения температуры холодного, причем влияние температур Т₁ и Т₂ на значение η_ц различно. Увеличение темпера­туры горячего источника в меньшей сте­пени повышает КПД цикла Карно, чем такое же (в Кельвинах) уменьшение тем­пературы холодного.

Являясь следствием второго закона термодинамики, формула для КПД цикла Карно, естественно, отражает его со­держание. Из нее видно, что теплоту горячего источника можно было бы пол­ностью превратить в работу, т.е. полу­чить КПД цикла, равный единице, лишь в случае, когда Т₁ → ∞, либо Т₂ → 0. Оба значения температур недостижимы. (Недостижимость абсолютного нуля температур следует из третьего начала термо­динамики)

При Т₁ = Т₂, термический КПД цикла равен нулю. На это указывает и КПД иде­ального цикла: невозмож­ность превращения теплоты в работу, если все тела системы имеют одинаковую температуру, т.е. находятся между собой в тепловом равновесии.

Следует иметь в виду, что коэффициент полезного действия теоретического цикла Карно всегда выше любого произвольного цикла, имеющего одинаковые максимальную и минимальную температуры рабочего тела.

Контрольные вопросы и задачи.

1. Возможен ли процесс, в котором теплота, подведенная от горячего источника, полностью превращается в работу?

2. Какой максимальный КПД теплового двигателя, работающего между температурами 400 и 18⁰С

3. Показать, что две адиабата не могут пересекаться друг с другом,

4.основные термодинамические процессы в газах

4.1. ТЕРМОДИНАМИЧЕСКИЕ ПРОЦЕССЫ ИДЕАЛЬНЫХ ГАЗОВ В ЗАКРЫТЫХ СИСТЕМАХ

Основными процессами, весьма важ­ными и в теоретическом, и в прикладном отношениях, являются: изохорный, протекающий при постоянном объеме (v = const); изобарный, протекающий при посто­янном давлении (р = const); изотермический, происходящий при постоянной темпера­туре (Т = const); адиабатный — процесс, при котором отсутствует теплообмен с окружа­ющей средой, и политропный, удов­летворяющий уравнению рvⁿ = const.

Метод исследования процессов, не зависящий от их особенностей и являю­щийся общим, состоит в следующем:

· выводится уравнение процесса, уста­навливающее связь между начальными и конечными параметрами рабочего тела в данном процессе;

· вычисляется работа изменения объема газа;

· определяется количество теплоты, подведенной (или отведенной) к газу в процессе;

· определяется изменение внутренней энергии системы в процессе;

· определяется изменение энтропии системы в процессе.

Изохорный процесс. При изохорном процессе выполняется условие dv=0 или v = const. Из уравнения состояния иде­ального газа (1.3) следует, что р/Т= R/v = const, т. е. давление газа прямо пропорционально его абсолютной темпе­ратуре:

(4.1)

На рис. 4.1 представлен график изохорного про­цесса. Работа расширения в этом процессе равна нулю, так как dv=0.

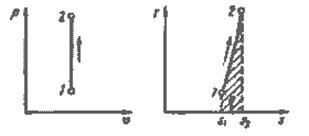
Рис.4.1. Изображение изохорного процесса в р-v и Т-s - координатах.

Количество теплоты, подведенной к рабочему телу в процессе 1-2 при v = const, определяется из соотношений (2.23):

(4.2)

Так как а = 0, то в соответствии с первым законом термодинамики Δu = q:

Δu =c_v (Т₂ – Т₁). (4.4)

Изменение энтропии в изохорном процессе определяется с учетом (3.6):

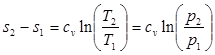(4.5)

Из (4.5) следует, что зависимость энтропии от температуры в изохорном процессе имеет логарифмический характер (рис.4.1).

Изобарный процесс. Из уравнения состояния идеального газа (1.3) при р = const находим, что v/T=R/p = const, или:

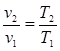. (4.6)

То есть, в изобарном процессе объем газа пропорционален его абсолютной температуре (закон Гей-Люссака, 1802 г.). На рис. 4.2 изображен график процесса.

Из выражения (2.6) следует, что:

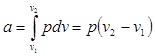(4.7)

Так как pv₁ = RT₁ и pv ₂= RT₂. то одновременно:

а = R (Т₂ – Т₁) (4.8)

Количество теплоты, сообщаемое га­зу при нагревании (или отдаваемое им при охлаждении), находим из уравнения (2.23):

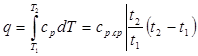(4.9)

где с_{р ср.} —средняя массовая изобарная теплоемкость в интервале темпера­тур от t₁ до t₂.

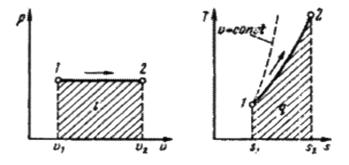
Рис.4.2. Изображение изобарного процесса в р-v и Т-s – диаграммах.

При с_р =const:

q = с_р (t₂- t₁) (4.10)

Изменение энтропии при с_р =const, согласно (3.5) равно:

, (4.11)

т. е. температурная зависимость энтро­пии при изобарном процессе тоже имеет логарифмический характер, но поскольку с_р > с_v, то изобара в Т-s -диаграмме идет более полого, чем изохора (правый график на рис.4.2).

Изотермический процесс. При изотермическом процессе температура постоян­на, следо

Date: 2015-05-09; view: 1940; Нарушение авторских прав