Задачи с решениями

1. По введенному натуральному числу п< 30000 найти значение выражения 2ⁿ.

Решение. Известно, что существует эффективный по количеству выполняемых действий умножения алгоритм возведения произвольного числа в натуральную степень. Однако при его реализации для больших значений степени п придется выполнять операцию умножения длинного числа на длинное, которая, как было показано в параграфе 4, требует порядка L² умножений, где L — количество цифр в каждом из «длинных» множителей.

Второй возможный подход к решению данной задачи — это перевод двоичного числа, состоящего из одной единицы и п нулей (а именно так в двоичной системе выглядит 2ⁿ), в десятичную систему счисления методом деления в двоичной системе на 10 = 1010₂. Но деление в двоичной системе придется организовывать самостоятельно (аналогично алгоритму деления длинного числа на короткое, разобранному в параграфе 6).

Наиболее же простым с точки зрения понимания и отладки программы является алгоритм простого последовательного умножения на некоторую степень двойки, являющуюся коротким числом. Приведем такое решение задачи, использующее процедуру mult из параграфа 3. Умножение здесь производится, пока это возможно, на 2¹⁷ (произведение 2¹⁷ на максимальную цифру 10000-ичной системы счисления — 9999, еще меньше, чем максимальное число, представимое в целом типе). Затем результат домножается на оставшееся 2^k, где k< 17.

Var

s: along; {данный тип определен в параграфе 1}

L,n,i,k: integer;

Begin

readln (n); {вводим значение степени}

s[1]:= 1; {результат для нулевой степени}

L:=1; {длина результата}

while n>16 do

{умножаем на 1 shl 17=2^17}

begin

mult(s,L,1 shl 17);

n:= n-17

end;

if n>0 then mult(s,L,1 shl n); {умножаем на оставшуюся степень}

assign(output,'output.txt');

rewrite (output);

write (s[L]); {старший разряд просто печатаем}

for i:=L-l downto 1 do

begin

k:=1000;

while s[i]<k do {недостающие цифры заменим 0}

begin

write(0);

k:=k div 10

end;

write(s[i])

end;

close(Output)

End.

2. Дана последовательность из не более чем 1000 неотрицательных целых чисел, каждое из которых удовлетворяет ограничению 0 < т < 2³¹. Числа записаны в позиционной системе счисления с основанием Р. Необходимо определить количество последних идущих подряд нулей в произведении этих чисел, записанном в той же системе счисления.

Решение. Один из возможных вариантов решения этой задачи заключается в прямом вычислении значения произведения этих чисел и определении количества хвостовых нулей в нем. Программа фактически будет состоять лишь из процедуры умножения «длинного» Р-ичного числа на «короткое», аналогичной описанной в параграфе 3, и может оказаться короче, нежели программа, реализующая алгоритм разложения на Р-ичные множители.

3. Вычислить с максимальной точностью значение выражения 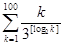. Результат записать в виде десятичной дроби.

Решение. Для того чтобы решить эту задачу точно, нужно понимать, на каких этапах вычисления значения суммы может возникать погрешность.

Так, если производить последовательное суммирование 100 дробей, представленных в одном из вещественных компьютерных типов (пусть даже в 80-разрядном), погрешность суммы может в 100 раз превысить погрешность представления каждой дроби в отдельности.

Кроме того, так как нас интересует лишь целая часть от логарифма натурального числа, то использовать операцию отбрасывания дробной части от значения логарифма, полученного в вещественной арифметике, также нельзя. В противном случае мы можем получить, например, для log₂4 вещественнее значение 1,9999999999, целая часть которого равна единице, вместо требуемой двойки. Поэтому вычисление целой части логарифма числа k следует проводить в цикле, используя исключительно целочисленную арифметику.

Turbo-Pascal:

log:=0;

i:=1;

while i<k do

begin

i:= i*2;

log:= log+1

end;

C:

log=0;

i = 1;

while (i<k)

{i*=2;

log++;

}

Тоже замечание касается и возведения тройки в целую степень.

Заметим, что при 1< k< 100, [1оg₂ k ] принимает значения от 1 до 6. Следовательно, сто обыкновенных дробей, которые требуется сложить, имеют всего 6 различных знаменателей: 3, З², З³,... З⁶, причем наименьшим общим знаменателем этих дробей является З⁶ (это число «короткое»). Поэтому несложно привести все 100 дробей к общему знаменателю и, используя лишь целочисленную арифметику, получить значение числителя и знаменателя результирующей дроби. Для перехода от обыкновенной дроби к десятичной можно воспользоваться алгоритмом деления «короткого» числа на «короткое», изложенном в параграфе 5, и определить точное значение искомой суммы.

Контрольные вопросы и упражнения

1. Как определить, достаточно ли для точного решения задачи стандартных компьютерных типов данных, или вычисления придется организовывать самому, с помощью алгоритмов «длинной» арифметики?

2. Назовите преимущества и недостатки различных способов представления «длинных» чисел.

3. Напишите программу для решения задачи 2 из параграфа 7.

4. Решите задачу 3 из параграфа 7 для случая, когда основанием логарифма является дробное число 1,9, а в знаменателе вместо степеней тройки стоят степени числа 3,1. Значение суммы по-прежнему должно быть вычислено точно.

5. Реализуйте алгоритм сложения двух знаковых «длинных» чисел. Для этого замените k -разрядное отрицательное число т на его дополнение до числа 10 ^k, то есть на число 10 ^k -| т |. Сделать это можно по алгоритму, аналогичному алгоритму получения дополнительного кода отрицательного двоичного числа. Обратным кодом десятичного числа является замена каждой его цифры i на (9- i). К обратному коду нужно прибавить единицу, чтобы получить дополнительный код. Если отрицательные слагаемые заменить на их дополнительные коды, то для сложения можно применить процедуру Add, приведенную в параграфе 2.

6. Реализуйте алгоритм целочисленного деления с остатком «длинного» числа на «длинное».

* В дальнейшем объяснении предусматривается, что читатель знает, как описываются данные, описание массивов и т.д., т.е. имеет навыки программирования и знаком с языком Turbo Pascal.