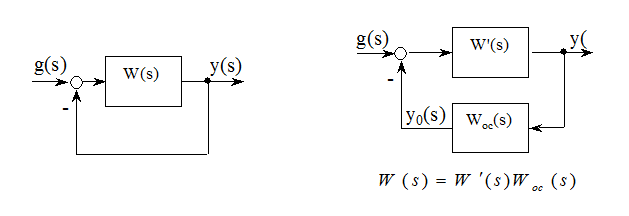
Свойства систем автоматического управления

Рассмотренная выше устойчивость (совместно с критериями ее определения) не является единственным свойством систем автоматического управления. Системы характеризуются: запасом устойчивости, областями устойчивости, притяжения, качеством регулирования и другими характеристиками. Рассмотрим некоторые из них.

Структурная устойчивость (неустойчивость)

Это такое свойство замкнутой системы, при наличии которого она не может быть сделана устойчивой ни при каких изменениях параметров.

Пусть . Годограф Найквиста для данной системы изображен на Рис.А. Устойчивость этой системы определяется значениями параметров и . Рассматриваемая система является структурно устойчивой.

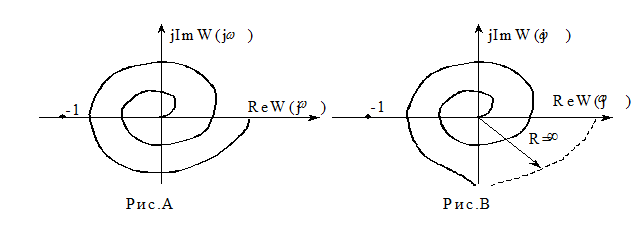
Пусть 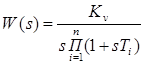. (Рис.В). Устойчивость также зависит от параметров 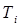и 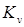. Система структурно устойчива.

Пусть 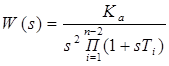. В любом случае (при любых значениях параметров) система будет неустойчива. То есть система является структурно неустойчивой.

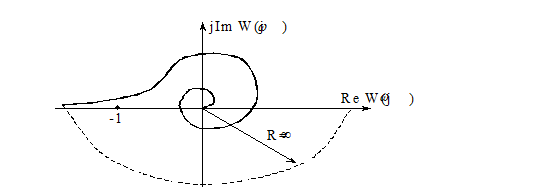
В частном случае передаточная функция имеет вид 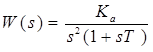. При этом соответствующее характеристическое уравнение замкнутой системы: 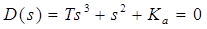. Нарушен принцип перемежаемости корней и полюсов. Система неустойчива. Структурно неустойчива.

Система с передаточной функцией 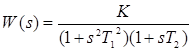- структурно неустойчива, так как для замкнутой системы 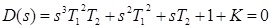, при этом коэффициенты 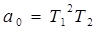, , 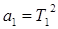, , 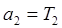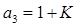- все положительны, но из условия 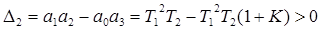следует, что 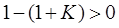, откуда 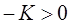, или 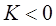. То есть система неустойчива.

Система 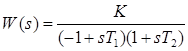также структурно устойчива. Здесь звено 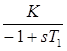- квазиапериодическое (статически неустойчиво). Характеристическое уравнение замкнутой системы 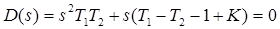. Откуда можно получить два граничных условия: 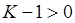и .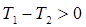

Для одноконтурных систем имеют место условия (Мейеров М.В.):

Пусть одноконтурная система состоит из:

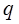- интегрирующих звеньев,

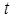- неустойчивых звеньев,

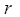- консервативных звеньев. Тогда при отсутствии в системе дифференцирующих звеньев она будет структурно устойчива в том случае, если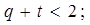

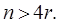
В случае многоконтурных систем соотношения Мейерова необходимо применять к каждому контуру, входящему в систему.

Date: 2015-05-08; view: 476; Нарушение авторских прав