
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Решения задач следует излагать подробно и аккуратно, объясняя и мотивируя все применяемые формулы, а также действия по ходу решения, и делая необходимые чертежи
|
|
РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА № 3
КОНТРОЛЬНЫЕ ЗАДАНИЯ ПО ФИЗИКЕ
(для студентов заочного отделения)
Коломна - 2015
Правила выполнения и оформления контрольных работ
При выполнении контрольных работ необходимо строго придерживаться указанных ниже правил. Перед выполнением контрольных задач изучить разбор подобной задачи, данных в начальных файлах. Работы, выполненные без соблюдения этих правил, не засчитываются и возвращаются на переработку.
1. Каждая контрольная работа должна быть выполнена в отдельной тетради в клетку чернилами любого цвета, кроме красного. На титульном листе работы (на обложке тетради) должны быть ясно написаны фамилия студента, учебный номер (шифр), номер контрольной работы, название дисциплины. Указать проверяющего. В конце работы следует поставить дату её выполнения и расписаться.
2. В работу должны быть включены все задачи, указанные в задании, строго по положенному варианту и в соответствии со списком группы до номера 9. Далее по цифре, стоящей за цифрой 1 (например, 13 – 3 вариант или 21 – 1 вариант)
Решения задач следует располагать в порядке номеров, указанных в заданиях, сохраняя номера задач, причем каждая следующая задача выполняется с новой страницы. Перед решением каждой задачи необходимо полностью выписать её условие.
Решения задач следует излагать подробно и аккуратно, объясняя и мотивируя все применяемые формулы, а также действия по ходу решения, и делая необходимые чертежи.
5. Номера задач выбирать по последней цифре своего шифра из таблицы плюс 1 задачу из раздела «Задачи для самостоятельного решения» с номером по строке таблицы своего варианта (если строка 0 варианта, то это 10 задача).
| Вариант | Номера задач | |||||||||
| 3 304 | 3 312 | 3 320 | 3 332 | 3 330 | 3 347 | |||||
| 3 306 | 3 309 | 3 322 | 3 335 | 53 537 | 3 340 | 3 344 | ||||
| 3 303 | 3 308 | 3 319 | 3 333 | 3 338 | 3 341 | 3 353 | ||||
| 3 305 | 3 310 | 3 324 | 3 334 | 3 337 | 3 343 | 3 340 | ||||
| 3 301 | 3 308 | 3 322 | 3 335 | 3 342 | 3 345 | |||||
| 3 303 | 3 307 | 3 321 | 3 343 | 3 347 | ||||||
| 3 305 | 3 310 | 3 323 | 3 334 | 3 344 | 3 353 | |||||
| 3 302 | 3 309 | 3 320 | 3 343 | 3 348 | ||||||
| 3 304 | 3 311 | 3 319 | 3 342 | 3 354 | ||||||
| 3 302 | 3 307 | 3 321 | 3 336 | 3 343 | 3 345 |
301. Два одинаковых заряжейных шарика подвешены в одной точке на нитях одинаковой длины. При этом нити разошлись на угол α. Шарики погружаются в масло плотностью ρ0=8×102 кг/м3. Какова диэлектрическая проницаемость ε масла, если угол расхождения нитей при погружений шариков в масло остается неизменным? 11лотностъ.материала шариков ρ = 1,6 ×103 кг/м3.
302. Расстояние d между двумя точечными зарядами q1= I мКл и q2 = - 1 мКл равно 10 см. Определить силу, действующую на точечный заряд q = 0,1 мКл, удаленный на 6 см от первого и на 8 см от второгозаряда.
303. Два одинаковых металлических заряженных шара находятся иа расстоянии г = 60 см. Сила отталкивания шаров F1 = 7× 10-5 Н. После того как шары приведи в соприкосновение и удалили друг от друга на прежнее расстояние, сила отталкивания возросла и стала равной F2 = 1.6×10-4 Н. Вычислить заряды q1 и q2, которые были нашарах до их соприкосновения. Диаметр шаров считать много меньшим расстояния между ними.
304. Два положительных точечных заряда q и 4 q закреплены на расстояния 60 см друг от друга. Определить, в какой точке на- прямой, проходящей через заряды, следует поместить третий заряд так, чтобы он находился в равновесии. Указать, какой знак должен иметь этот заряд для того, чтобы равновесие было устойчивым, если перемещения заряда возможны только вдоль прямой, проходящей через закрепленные заряды.
305. Четыре одинаковых положительных точечных заряда q= 10 нКл закренлены в вершинах квадрата со стороной а = 20 см. Найти силу F, действующую на один из этих зарядов со стороны трех остальных.
306. В вершинах квадрата находятся одинаковые заряды q = -3 × 10 -10 Кл каждый. Какой отрицательный заряд q1 нужно поместить в центре квадрата, чтобы сила взаимного отталкивания положительных зарядов была уравновешена силой притякения отрицательного заряда?
307. Тонкий прямой стержень длиной 10 см равномерно заряжен с линейной плотностью заряда t = 10-7 Кл /м. На продолжении оси стержня, на расстоянии а =10 см от ближайшего конца, находится точечный заряд q = 10-8 Кл. Определить силу. взаимодействия стержня и точечного заряда.
308. На продолжении оси тонкого прямого стержня равномерно заряженного
с линейной плотвостыо заряда t = 1 нКл/см на расстоя-
нии а = 10 см от конца стержня находится точечный заряд q
= 0.1 мКл. Второй, конец стержня уходит в бесконечность. Оцределить, силу взаимодействия стержня и точечного заряда.
309. Тонкий длинный стержень раномерно заряжен с линейной
плотностью t = 0,2 мКл/см. Определить силу, действующую на то-
чечный зяряд q = 10 нКл, иаходящийся на расстоянии г = 2 см, от
стержня вблизи его середины.
'
310.Тонкое полукольцо радиусом г = 10 см несет равномерно распределенный заряд
q = 0,2 мкКл,. В центре кривизны полукольца находится точечный заряд q = 10 нКл,
Найти силу взаимодействия точечного заряда и заряженного полукольца.
311. Заряд q = 10 нКл равномерно распределен по тонкому кольцу радиусом
г = 10 см. Определить силу взаимодействия заряженно го кольца с точечным -
зарядом q =0,5 нКл, находящимся на оси кольца на расстояний а = 10 см от его центра.
312. На тонком кольце равномерно распределен заряд с линейной плотностью заряда
t = 20 нКл/см. Радиус кольца г = 5см. На пер пендикуляре к плоскости кольца,
восстановленном из его середины, находится точечный заряд q = 40 нКл. Определить силу, действующую на точечный заряд со стороны заряженного кольца,
если он удален от центра кольца'на: 1) а1 = 10 см 2). а2 = 2 м.
313. Две длинные прямые параллельные нити находятся на расстоянии 10 см друг
от друга. На нитях, равномерно распределены заряды с линейными плотностями
t1 = - 2 нКл/см и t2 = 4 нКл/см. Опре делить напряженность электрического поля
Е в точке, удаленной от первой нити на расстояние г1 = б сми от второй, на
расстояние г2 = 8 см.
314. С какой силой (на единицу длины) взаимодействуют две заряженные бесконечно
длинные параллельные нити с одинаковой линейной плотностью заряда
t = 2×10-6 Кл/м, находящиеся на расстоянии 4 см друг от друга?
315. Поверхностная плотность заряда бесконечна протяженной вертикальной плоскости σ = 9,8×10-5 Кл/мг. К плоскости на нити под-
вешен заряженный шарик массой 10 г. Определить заряд q ша-
рика, если нить образует с плоскостью угол ф = 45°.
316. С какой силой на единицу площади взаимодействует две бесконечные
параллельные плоскости заряженные с одинаковой поверхностной плотностью
заряда σ = 2 • 10-б Кл/м2?
317. Параллельно бесконечной плоскости, заряженной с поверх-
ностной плотностью заряда σ = 10-6 Кл/м2 расположена бесконечно
длинная прямая нить, заряженная с линейной плотностью t = Ю-8 Кл/м, Определить силу, действующую со стороны плоскости на единицу длины нити.
З18. На бесконечном тонкостенном цилиндре диаметром 10 см равномерно
распределен заряд с поверхностной плотностью σ = 10-6 Кл/м. Определить
напряженность поля в точке, отстоящей от поверхности цилиндра на а =5 см.
319. Определить потенциальную энергию системы двук точечных зарядов q1 = 10-7 Кл и q2 = 10-8 Кл, находящихся на расстоянии 10 см друг от друга.
320. Электрическое поле образовано бесконечно длинной нитью, заряженной с линейной плотностью t = 10-10 Кл/м. Определить разность потенциалов U двух точек поля, отстоящих от нити на расстоянии r1 = 5 см и г2 = 10 см.
321. Поле образовано бесконечной равномерно заряженной плоскостью с поверхностной плотностью заряда σ = 10-8 Кл/м2. Определить разность потенциалов U двух точек поля,
отстоящих от плоскости на r1 = 5 см и г2 = 10 см.
322. Две параллельные плоскости, заряженные с поверхностными плотностями σ1 = 0,2 мкКл/м2 и σ2 = - 0,3 мкКл/м2, находятся на рас стоянии 0,5 см друг от друга.
Определить разность потенциалов между плоскостями.
323. Поле образовано точечным диполем с электрическим мо ментом р = 10-10 Кл×м.
Определить разность потенциалов U двух точек поля, расположенных симметрично относительно диполя на его оси, на расстоянии10 см от центра диполя.
324. Тонкая квадратная рамка равномерно заряжена с линейной плотностью заряда
t = 10-10 Кл/м. Определить потенциал j поля в точке пересечения диагоналей.
325. Пылинка массой 10 -9 г, несущая на себе 5 электронов, прошла в вакууме ускоряющую
разность потенциалов U = 3×105 В. Какова кинетическая энергия пылинки? Какую
скорость приобрела пылинка?
326. Электрон, обладающий кинетической энергией Т = 5 эВ влетел в однородное электри-
ческое поле в направлении силовых линий поля. Какой скоростью будет обладать электрон, пройдя в этом поле разность потенциалов U = 2 В?.
327. Ион атома водорода Н+ прошел разность потенциалов U1 = 100 В, а ион атома калия К+ U2 = 200 В. Найти отношение скоростей этих ионов.
328. Найти отношение скоростей ионов Са++ и Nа+, прошедших одинаковую разность
потенциалов.
329. Пылинка массой m = 10-5 г, несущая на себе заряд q = 10-8 Кл влетела в электрическое поле в направлении силовых линий. После прохождения разности потенциалов
U = 160 В пылинка приобрела скорость v = 20 м/с. Какая была скорость пылинки до того, как она взлетела в поле?
330. Электрон с энергией Т = 100 В (в бесконечности) движется вдоль силовой
линии по направлению к поверхности металлической заряженной сферы радиусом R = 5см.
Определить минимальное расстояние, на которое приблизится электрон к поверхности сферы, если ее заряд q = - 10-9 Кл.
331. Два конденсатора емкостью С1 = 2 мкФ и С2 = 3 мкФ соединены последовательно и присоединены к батарее э.д.с. Е = 30 В. Определить заряд каждого конденсатора
и разность потенциалов между его обкладками.
332. Пространство между пластинами плоского конденсатора заполнено двумя слоями диэлектриков: слоем стекла толщиной d1 =1 см и слоем парафина
толщиной d2 = 2 см. Разность тютенциалов между обкладками U = 3000 В. Определить напряженность поля и падение потенциала в каждом из слоев.
333. Плоский конденсатор состоит из двух круглых пластин ра диусом г = 20 см
каждая. Расстояние между пластинами d =5 мм. конденсатор присоединен к источнику напряжения U = 3000 В. Определить заряд и напряженность поля конденсатора, если диэлектриком будут: а) возду; б) стекло.
334. К воздушному конденсатору, заряженному до разности потенциалов U1 = 500 В и отключенному от источника напряжения присоединили параллельно второй конденсатор таких же размерови формы, но с другим диэлектриком (стекло). Определить диэлектрическую проницаемость ε стекла, если после присоединения второго конденсатора разность потенциалов уменьшилась до U2 = 70 В.
335. Плоский конденсатор с площадью пластин S = 300 см каждая заряжен до разности потенциалов U = 1000 В. Расстояние между, пластинами d = 4 см. Диэлектрик - стекло. Определить энергию W поля конденсатора и плотность w энергии поля.
336. Расстояние между пластинами плоского конденсатора d = 2 см, разность потенциалов U = 6000 В. Заряд каждой пластины q = 10-8 Кл. Определить энергию W поля конденсатора и силу F взаимного притяжения пластин.
337. Определить.плотность тока j железной прволоке длиной, му если проволока находится под напряжением U = 6 В.
338. Катушка и амперметр соединены последовательно и присоединены к источнику тока. К клеммам катушки присоединен вольтметр с сопротивлением г = 2000 Ом. Амперметр показывает I = 0,25А, вольтметр U = 100 В. Определить сопротивление катушки. Сколько процентов составит ошибка, если при определении сопротивления катушки не будет учтена проводимость вольтметра?
339. В ееть с напряжением U = 120 В включили катушку с сопротивлением г = 5000 Ом и вольтметр, соединенные последовательно. Показание вольтметра U = 80 В. Когда взятую катушку заменили другой, вольтметр показал U = 50 В. Определить сопротивление другой катушки.
340. Э. д.с. батарей Е = 12 В. Наибольшая сила тока, которую может дать батарея, Iмакс = 6 А. Определить максимальную мощность Рмакс, которая может выделяться во внешней цепи.
341. Э. д. с. батареи Е = 6О В, внутреннее сопротивление гi = 4 Ом. Внешняя цепь потребляет мощность N =125 Вт. Определить силу тока I в цепи, напряжение U, под которым находится внешняя цепь, и ее сопротивление г.
342. Э. д. с. батареи Е= 8 В. При силе тока 1=2 А к. п. д. батареи η = 0,75. Определить внутреннее сопротивление гi батареи.
342. В проводнике за время t =10 с при равномерном возрастании тока от I1 = 0 до I2 =2 А выделилось Q =2 кДж теплоты. Найти сопротивление г проводника.
343. По проводнику, сопротивлением г = 3 Ом течёт равномерно возрастающий ток. За время t = 8 с в проводнике выделилась теплота Q = 200 Дж. Определить заряд q, протекший за это время по проводнику. В момент времени принятый за начальный, ток в проводнике был равен нулю.
344. Ток в проводнике сопротивлением г = 100 Ом за время t =30 с равномерно нарастает от I1 = 0 до I2 = 10 А. Определить теплоту Q, выделившуюся за это время в проводнике.
345. Ток в проводнике сопротивлением г = 100 Ом за время t =30 с равномерно нарастает от I1 = 0 до I2 = 10 А. Определить теплоту Q, выделившуюся за это время в проводнике.
346. Ток в проводнике сопротивлением г = 15 Ом за время t = 5 с равномерно возрастает от нуля до некоторого максимума. За это время в проводнике выделилась теплота Q = 104 Дж. Определить среднее значение силы тока < I > в проводнике за этот промежуток времени.
347. Ток в проводнике равномерно увеличивается от нуля до некоторого максимального значения в течение t =10 с. За это время в проводнике выделилась теплота Q = 103 Дж. Определить скорость нарастания тока в проводнике, если сопротивление его г = 3 Ом.
348. Ток в проводнике.сопротивлением г = 12 Ом, равномерно убывает от I1 = 5 А до I2 = 0 в течение t =10 с, Определить теплоту Q выделившуюся в этом проводнике за указанный промежуток времени.
|
|
Рис.18
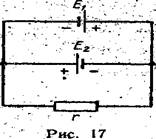
349. Два источника тока Е1 = 14 В с внутренн им сопротивлением г1 = 2 Ом,
и Е2 = 6 В с внутренним сопротивлением г2 = 4 Ом,. а также реостат г = 10 Ом
соединены как показано на рис. 17. Определить сильг токов в реостате
и в источниках тока,
350. Сопротивление г = 4 Ом подключено к двум параллельно соединенным источникам тока с э;д.с. Е1 = 2,2 В и Е2 = 1,4 В и внутренним сопротивлением г1 = 0,6 Ом и г2 = 0,4 Ом. Определить ток в сопротивлении г и напряжение на зажимах второго источника тока.
351. Определить силу тока в каждом элементе и напряжение на зажимах реостата г = 50 Ом, к которому параллельно подсоединены два источника э.д.с. Е1 = 8 В и Е2 = 4 В. Их внутренние сопротивления г1 = 1 Ом и г2 = 0,5 Ом соответственно.
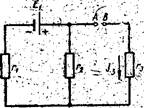
352. Три сопротивления г1 = 5 Ом, г2 = 1 Ом и г3 = 3 Ом, а также
источник тока Е1 = 1,4 В соединены, как показано на рис. 18. Определить э. д. с.
источника, который надо подключить в цепь между точками А и В,
чтобы в сопротивлёнии г3 шел ток силой 1А в на правлении, указанном стрелкой.
Сопротивлением источников тока пренебречь.
353. Определить силу тока в сопротивлении г3 (рис. 19) и на пряжение на -
концах этого сопротивления; если Е1 = 4 В, Е2 = 3 В, г1= 2 Ом, г2 =6 Ом, г3 = 1 Ом.
Внутренними сопротивлениями источников тока пренебречь.
354. Две батареи (Е1 = 10 В, г1 = 1 Ом, Е2 =8 в, г2 = 2 Ом) и рео стат (г = 6 Ом)
соединены, как показано на рис. 17. Определить силу тока в батареях и реостате
Date: 2015-05-08; view: 909; Нарушение авторских прав