
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Коэффициент переноса. Фундаментальное уравнение теории транзисторов
|
|
Коэффициент передачи эмиттерного тока a характеризует изменение коллекторного тока I к при вызвавшем его изменении эмиттерного тока I э.
Ток коллектора обусловлен дырками, дошедшими от эмиттерного перехода до коллекторного. Поэтому важны доля дырок, дошедших до коллекторного перехода и нерекомбинировавших в базе, и доля дырочного тока в эмиттерном токе.
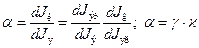 . (5.9)
. (5.9)
Зависимость коэффициента инжекции g от параметров биполярного транзистора была получена ранее. Рассмотрим зависимость коэффициента переноса 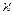 от параметров биполярного транзистора.
от параметров биполярного транзистора.
Из уравнения непрерывности
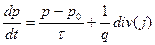 (5.10)
(5.10)
следует, что в стационарном режиме
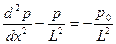 . (5.11)
. (5.11)
Решение дифференциального уравнения (5.11) в общем виде будет иметь следующий вид:
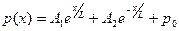 . (5.12)
. (5.12)
Запишем граничные условия для (5.11) исходя из того, что заданы эмиттерный ток J эр = g J э и коллекторное напряжение U к.
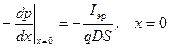 , (5.13)
, (5.13)
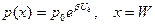 . (5.14)
. (5.14)
Найдем коэффициенты А 1 и А 2.
Продифференцировав уравнение в решении (5.12) по x, получаем:
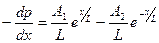 ,
,
с учетом граничных условий (5.13) имеем:
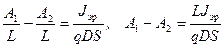 , (5.15а)
, (5.15а)
с учетом граничных условий (5.15а) имеем:
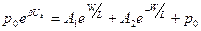 . (5.15б)
. (5.15б)
Решая совместно уравнения (5.15а, б), находим коэффициенты A 1 и A 2. Затем подставляем A 1 и A 2 в уравнение (5.12) и получаем следующее выражение для распределения концентрации инжектированных дырок р n(х) по базе биполярного транзистора:
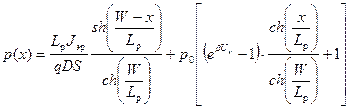 . (5.16)
. (5.16)
Последний сомножитель в квадратных скобках уравнения (5.16) всегда меньше единицы.
Наконец, разложив гиперболический синус sh (x) и гиперболический косинус ch (х) в ряд при условии x < W << L р, получаем закон распределения дырок р n(х) по базе биполярного транзистора в первом приближении:
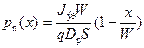 . (5.17)
. (5.17)
Выражение (5.17) показывает, что в первом приближении распределение дырок р n(х) по толщине базы линейно. Этот вывод понятен и по физическим соображениям. Поскольку ток в базовой области диффузионный и примерно постоянен по ширине базы (так как рекомбинация мала), градиент концентрации дырок постоянен: 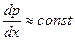 .
.
Так как коэффициент переноса
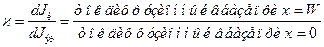 ,
,
то
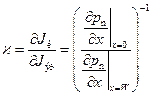 .
.
Для того, чтобы точно определить коллекторный ток J к, продифференцируем уравнение (5.16) для концентрации дырок р (х) и рассчитаем это выражение при х = W. Тогда
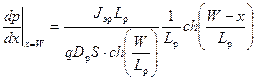 . (5.18)
. (5.18)
Умножив (5.18) на qDS, получаем с учетом того, что гиперболический 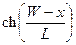 стремится к единице,
стремится к единице,
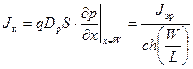 . (5.19)
. (5.19)
Следовательно, коэффициент переноса 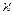 имеет вид:
имеет вид:
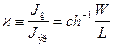 . (5.20)
. (5.20)
Уравнение (5.20) является очень важным соотношением для биполярных транзисторов и по этой причине называется фундаментальным уравнением теории транзисторов.
Разлагая гиперболический косинус ch (x) в ряд при условии, что x < W, и используя первый член в этом разложении, получаем:
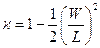 . (5.21)
. (5.21)
Полагая значение W = 0,2 L, получаем:
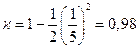 .
.
Таким образом, значение коэффициента переноса 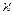 будет составлять величину, близкую к единице (отличие не более 2%) при условии, что ширина базы биполярного транзистора W по крайней мере в 5 раз меньше, чем диффузионная длина.
будет составлять величину, близкую к единице (отличие не более 2%) при условии, что ширина базы биполярного транзистора W по крайней мере в 5 раз меньше, чем диффузионная длина.
Поскольку коэффициент передачи a определяется произведением коэффициентов инжекции g и переноса 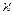 как
как 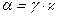 , то у сплавных транзисторов, где ширина базы составляет W = 10¸20 мкм, в коэффициенте передачи a главную роль играет коэффициент переноса
, то у сплавных транзисторов, где ширина базы составляет W = 10¸20 мкм, в коэффициенте передачи a главную роль играет коэффициент переноса 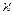 . У диффузионных транзисторов ширина базы равняется W = (1¸2) мкм и главную роль в коэффициенте передачи a играет коэффициент инжекции g.
. У диффузионных транзисторов ширина базы равняется W = (1¸2) мкм и главную роль в коэффициенте передачи a играет коэффициент инжекции g.
Date: 2015-05-05; view: 620; Нарушение авторских прав