
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

ГОСТ 27. 002—89 С. 29
|
|
К терминам «Единичный показатель надежности» и «Комплексный показатель надежности» (пп. 6.2; 6.3)
В отличие от единичного показателя надежности комплексный показатель надежности количественно характеризует не менее двух свойств, составляющих надежность, например безотказность и ремонтопригодность. Примером комплексного показателя надежности служит коэффициент готовности (п. 6.26) Кг, стационарное значение которого (если оно существует) определяют по формуле
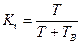
где Т — средняя наработка на отказ (п. 6.11 );
Т в — среднее время восстановления (п. 6.21).
К терминам «Расчетный показатель надежности», «Экспериментальный показатель надежности», «Эксплуатационный показатель надежности», «Экстраполированный показатель надежности»
(пп. 6.4; 6.5; 6.6; 6.7)
Такую классификацию показателей надежности вводят в зависимости от способов их получения. Аналогичная классификация содержится в международных документах ИСО, МЭК и ЕОКК [4-—6]. Наличие этих понятий должно предупредить путаницу, которая имеет место на практике при обсуждении численных данных, полученных разными способами и на разных стадиях жизненного цикла объекта.
К термину «Вероятность безотказной работы» (п. 6.8)
Вероятность безотказной работы определяется в предположении, что в начальный момент времени (момент начала исчисления наработки) объект находился в работоспособном состоянии. Обозначим через t время или суммарную наработку объекта (в дальнейшем для краткости называем (просто наработкой). Возникновение первого отказа — случайное событие, а наработка т от начального момента до возникновения этого события — случайная величина. Вероятность безотказной работы Р(t) объекта в интервале от 0 до t включительно определяют как
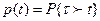 . (1)
. (1)
Здесь Р{•}— вероятность события, заключенного в скобках. Вероятность безотказной работы P (t) является функцией наработки t. Обычно эту функцию предполагают непрерывной и дифференцируемой.
Если способность объекта выполнять заданные функции характеризуется одним параметром v, то вместо (1) имеем формулу
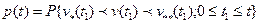 , (2)
, (2)
где v* и v**— предельные по условиям работоспособности значения параметров (эти значения, вообще, могут изменяться во времени).
Аналогично вводят вероятность безотказной работы в более общем случае, когда состояние объекта характеризуется набором параметров с допустимой по условиям работоспособности областью значений этих параметров [8].
Вероятность безотказной работы Р(t) связана с функцией распределения F(t) и плотностью распределения f(t) наработки до отказа:
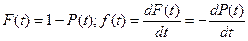 . (3)
. (3)
С. 30 ГОСТ 27.002—89
Наряду с понятием «вероятность безотказной работы» часто используют понятие «вероятность отказа», которое определяется следующим образом: это вероятность того, что объект откажет хотя бы один раз в течение заданной наработки, будучи работоспособным в начальный момент времени. Вероятность отказа на отрезке от 0 до t определяют по формуле
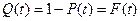 . (4)
. (4)
Точечные статистические оценки для вероятности безотказной работы 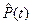 от 0 до t и для функции распределения наработки до отказа
от 0 до t и для функции распределения наработки до отказа 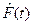 даются формулами:
даются формулами:
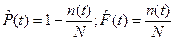 , (5)
, (5)
где N — число объектов, работоспособных в начальный момент времени;
п(t) — число объектов, отказавших на отрезке от 0 до t.
Для получения достоверных оценок объем выборки N должен быть достаточно велик [2, 3, 7].
Определение безотказной работы в соответствии с формулами (1) и (2) относится к объектам, которые должны функционировать в течение некоторого конечного отрезка времени. Для объектов одноразового (дискретного) применения вероятность безотказной работы определяют как вероятность того, что при срабатывании объекта отказ не возникает. Аналогично вводят вероятность безотказного включения (например в рабочий режим из режима ожидания).
К терминам «Гамма-процентная наработка до отказа», «Гамма-процентный ресурс», «Гамма-процентный срок службы», «Гамма-процентное время восстановления», «Гамма-процентный срок сохраняемости» (пп. 6.9; 6.15; 6.20; 6.24)
Перечисленные показатели определяют как корни tγ уравнения
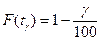 , (6)
, (6)
где F (t) — функция распределения наработки до отказа (ресурса, срока службы).
В частности, гамма-процентную наработку до отказа tγ определяют из уравнения
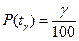 ,
,
где Р(t) — вероятность безотказной работы.
Как видно из формулы (6), гамма - процентные показатели равны квантилям соответствующих распределений. Если вероятности, отвечающие этим квантилям, выражают в процентах, то для показателей безотказности обычно задают значения 90; 95; 99; 99,5% и т. д. Тогда вероятность возникновения отказа на отрезке [0; t] будет составлять 0,10; 0,05; 0,01; 0,005 и т. д. Задаваемые значения γ для критических отказов должны быть весьма близки к 100%, чтобы сделать критические отказы практически невозможными событиями. Для прогнозирования потребности в запасных частях, ремонтных мощностях, а также для расчета пополнения и обновления парков машин, приборов и установок могут потребоваться гамма - процентные показатели при более низких
ГОСТ 27.002—89 С. 31
значениях γ, например при γ = 50%, что приближенно соответствует средним значениям.
Статистические оценки для гамма-процентных показателей могут быть получены на основе статистических оценок либо непосредственно, либо после аппроксимации эмпирических функций подходящими аналитическими распределениями. Необходимо иметь в виду, что экстраполирование эмпирических результатов за пределы продолжительности испытаний (наблюдений) без привлечения дополнительной информации о физической природе отказов может привести к значительным ошибкам.
К терминам «Средняя наработка до отказа», «Средний ресурс», «Средний срок службы», «Среднее время восстановления», «Средний срок сохраняемости» (пп. 6.10; 6.16; 6.18; 6.21; 6.25)
Перечисленные показатели равны математическим ожиданиям соответствующих случайных величин, наработки до отказа, ресурса, срока службы, времени восстановления, срока сохраняемости.
Среднюю наработку до отказа Т1 вычисляют по формуле
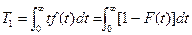 ,
,
где F(t) — функция распределения наработки до отказа,
f(t) — плотность распределения наработки до отказа.
С учетом (3) T1, выражается через вероятность безотказной работы:
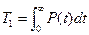 .
.
Статистическая оценка для средней наработки до отказа дается формулой
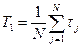 . (7)
. (7)
Здесь N — число работоспособных объектов при t= 0,
τj — наработка до первого отказа каждого из объектов.
Формула (7) соответствует плану испытаний, при котором все объекты испытываются до отказа [2, 3, 7].
К термину «Средняя наработка на отказ» (п. 6.11)
Этот показатель введен применительно к восстанавливаемым объектам, при эксплуатации которых допускаются многократно повторяющиеся отказы. Очевидно, что это должны быть несущественные отказы, не приводящие к серьезным последствиям и не требующие значительных затрат на восстановление работоспособного состояния. Эксплуатация таких объектов может быть описана следующим образом: в начальный момент времени объект начинает работать я продолжает работать до первого отказа; после отказа происходит восстановление работоспособности, и объект вновь работает до отказа и т. д. На оси времени моменты отказов образуют поток отказов, а моменты восстановлений — поток восстановлений. На оси суммарной наработки (когда время восстановления не учитывается) моменты отказов образуют поток отказов. Полное и строгое математическое описание эксплуатации объектов по этой схеме построено на основе теорий восстановления [2, 7].
С. 32 ГОСТ 27.002—89
Определению средней наработки на отказ Т, которое приведено в данном стандарте, соответствует следующая формула
 . (8)
. (8)
Здесь t —суммарная наработка, r (t) — число отказов, наступивших в течение этой наработки, М{г(t)}—математическое ожидание этого числа. В общем случае средняя наработка на отказ оказывается функцией t. Для стационарных потоков отказов средняя наработка на отказ от t не зависит.
Статистическую оценку средней наработки на отказ 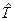 вычисляют по формуле, которая аналогична формуле (8)
вычисляют по формуле, которая аналогична формуле (8)
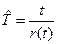 . (9)
. (9)
В отличие от формулы (8) здесь г(t) — число отказов, фактически происшедших за суммарную наработку t.
Формула (9) допускает обобщение на случай, когда объединяются данные, относящиеся к группе однотипных объектов, которые эксплуатируются в статистически однородных условиях. Если поток отказов — стационарный, то в формуле (9) достаточно заменить t на сумму наработок всех наблюдаемых объектов и заменить г(t) на суммарное число отказов этих объектов [3].
К терминам «Интенсивность отказов» и «Интенсивность восстановления» (пп. 6.12; 6.22)
Интенсивность отказов λ(t) определяют по формуле
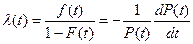 . (10)
. (10)
Для высоконадежных систем Р(t)≈1, так что интенсивность отказов приближенно равна плотности распределения наработки до отказа.
Статистическая оценка для интенсивности отказов 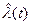 имеет вид
имеет вид
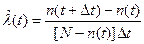 , (11)
, (11)
где использованы те же обозначения, что и в формуле (5).
Аналогично вводится интенсивность восстановления.
К терминам «Параметр потока отказов» и «Осредненный параметр потока отказов» (пп. 6.13; 6.14)
Параметр потока отказов μ(t) определяют по формуле
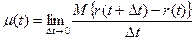 , (12)
, (12)
где ∆t— малый отрезок наработки,
r(t) — число отказов, наступивших от начального момента времени до достижения наработки t.
Разность г(t+∆t)-г(t) представляет собой число отказов на отрезке ∆t.
ГОСТ 27.002—89 С. 33
Наряду с параметром потока отказов в расчетах и обработке экспериментальных данных часто используют осредненный параметр потока отказов
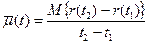 , (13)
, (13)
По сравнению с формулой (12) здесь рассматривается число отказов за конечный отрезок [t1, t2], причем t1≤t≤t2. Если поток отказов стационарный, то параметры, определяемые по формулам (12) и (13) от t не зависят.
Статистическую оценку для параметра потока отказов μ(t) определяют по формуле
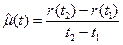 , (14)
, (14)
которая по структуре аналогична формуле (13). Для стационарных потоков, можно применять формулу
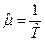 ,
,
где 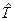 — оценка (8) для средней наработки на отказ.
— оценка (8) для средней наработки на отказ.
В международных документах ИСО, МЭК и ЕОКК термину «параметр потока отказов» соответствует термин failure intensity, в то время как термину «интенсивность отказов» (п. 6.12) соответствует термин failure гаtе. Это необходимо учитывать при использовании англоязычных источников, а также переводной литературы.
К терминам «Вероятность восстановления», «Гамма-процентное время восстановления», «Среднее время восстановления», «Интенсивность восстановления», «Средняя трудоемкость восстановления»
(пп. 6.19; 6.20; 6.21; 6.22; 6.23)
Для комплексной оценки ремонтопригодности допускается дополнительно использовать показатели типа удельной трудоемкости ремонта и удельной трудоемкости технического обслуживания.
К терминам «Коэффициент готовности», «Коэффициент оперативной готовности», «Коэффициент технического использования», «Коэффициент сохранения эффективности» (пп. 6.26; 6.27; 6.28; 6.29)
Коэффициент готовности характеризует готовность объекта к применению по назначению только в отношении его работоспособности в произвольный момент времени. Коэффициент оперативной готовности характеризует надежность объекта, необходимость применения которого возникает в произвольный момент времени, после которого требуется безотказная работа в течение заданного интервала времени. Различают стационарный и нестационарный коэффициенты готовности, а также средний коэффициент готовности [3, 5, 6].
Коэффициент технического использования характеризует долю времени нахождения объекта в работоспособном состоянии относительно общей продолжительности эксплуатации. Коэффициент сохранения эффективности характеризует степень влияния отказов на эффективность его применения по назначению. Для каждого конкретного типа объектов содержание понятия эффективности и точный смысл показателя (показателей) эффективности задаются техническим заданием и вводятся в нормативно-техническую и (или) конструкторскую (проектную) документацию.
С. 34 ГОСТ 27.002—89
К термину «Резервирование» (п. 7.1)
Резервирование — одно из основных средств обеспечения заданного уровня надежности объекта при недостаточно надежных компонентах и элементах. Цель резервирования — обеспечить безотказность объекта в целом, т. е. сохранить его работоспособность, когда возник отказ одного или нескольких элементов [11]. Наряду с резервированием путем введения дополнительных (резервных) элементов находят широкое применение другие виды резервирования. Среди них временное резервирование (с использованием резервов времени), информационное резервирование (с использованием резервов информации), функциональное резервирование, при котором используется способность элементов выполнять дополнительные функции или способность объекта перераспределять функции между элементами, нагрузочное резервирование, при котором используется способность элементов воспринимать дополнительные нагрузки сверх номинальных, а также способность объекта перераспределять нагрузки между элементами.
К терминам «Нормирование надежности», «Нормируемый показатель надежности» (пп. 8.1; 8.2)
При выборе номенклатуры нормируемых показателей надежности необходимо учитывать назначение объекта, степень его ответственности, условия эксплуатации, характер отказов (внезапные, постепенные и т. п.), возможные последствия отказов, возможные типы предельных состояний. При этом целесообразно, чтобы общее число нормируемых показателей надежности было минимально; нормируемые показатели имели простой физический смысл, допускали возможность расчетной оценки на этапе проектирования, статистической •опенки и подтверждения по результатам испытаний и (или) эксплуатации [10, 11].
При обосновании численных значений нормируемых показателей надежности необходимо руководствоваться принципом оптимального распределения затрат на повышение надежности, техническое обслуживание и ремонт.
Значения нормируемых показателей надежности учитываются, в частности, при назначении гарантийного срока эксплуатации (гарантийной наработки, гарантийного срока хранения), которые являются технико-экономическими (отчасти коммерческими) характеристиками объекта и не относятся к показателям надежности. Гарантийные сроки, показатели надежности и цена объекта должны быть взаимоувязаны.
Длительность гарантийного срока эксплуатации (гарантийной наработки, гарантийного срока хранения) должна быть достаточной для выявления и устранения скрытых дефектов и определяется соглашением между потребителем (заказчиком) и поставщиком (изготовителем).
К термину «Программа обеспечения надежности» (п. 9.1)
Программа обеспечения надежности — важнейший документ, служащий организационно-технической основой для создания объектов, удовлетворяющих заданным требованиям по надежности. Программа должна охватывать все или отдельные стадии жизненного цикла объекта.
Программа обеспечения надежности включает, в частности, программу экспериментальной отработки, которая определяет цели, задачи, порядок проведения и необходимый объем испытаний или экспериментальной отработки, а также регламентирует порядок подтверждения показателей надежности на стадии разработки. Программа обеспечения ремонтопригодности устанавливает комплекс взаимосвязанных организационно-технических требований и мероприятий, направленных на обеспечение заданных требований по ремонтопригодности и (или) повышения ремонтопригодности. Она разрабатывается одновременно с программой обеспечения надежности и является либо ее составной честью, либо самостоятельной программой [1].
ГОСТ 27.002—89 С. 35.
К термину «Испытания на надежность» (п. 10.1)
Испытания на надежность относятся к числу важнейших составных частей роботы обеспечению и повышению надежности технических объектов Эти испытаний в зависимости от контролируемых (оцениваемых) свойств, составляющих надежность, могут состоять из испытаний на безотказность долговечность, ремонтопригодность и сохраняемость. В частности, ресурсные испытания относятся к испытаниям на долговечность.
Планирование испытаний и обработка их результатов проводятся с применением методов математической статистики [2, 3, 7, 10] Оценивание значений показателей надежности при определительных испытаниях должно проводиться с заданной точностью (т. е. при заданной относительной погрешности) и с заданной достоверностью (т. е. при заданном уровне доверительной вероятности). Аналогичные требования предъявляются к контрольным испытаниям. Ускорение (форсирование) испытаний не должно приводить к снижению точности и достоверности оценок.
С. 36 ГОСТ 27.002—89
Date: 2015-05-05; view: 787; Нарушение авторских прав