
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Примеры решения задач. 1. Расстояние между предметом и его действительным изображением, даваемым линзой, L
|
|
1. Расстояние между предметом и его действительным изображением, даваемым линзой, L. Линейное увеличение равно k. Найти фокусное расстояние линзы.
| Дано: L, k, f =? |
Решение:
Построим изображение в линзе (см. рис.4)

| ||
| Рис. 4 |
Линейное увеличение определяется условием: k = (A’ B’) / (AB).
Исходя из подобия треугольников D АВО и D A’ B’ О получим
(A’ B’) / (AB) = b / a.
По условию задачи L = a + b.
Поэтому 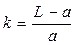 Þ
Þ 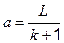 .
.
Учитывая, что 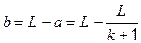 , преобразуем формулу тонкой линзы
, преобразуем формулу тонкой линзы
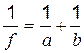 к виду
к виду 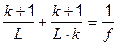 .
.
Отсюда приходим к ответу: 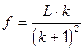 .
.
2. Две щели находятся на расстоянии 0,1 мм друг от друга и отстоят на 1,2 м от экрана. От удаленного источника на щели падает свет длиной волны 500 нм. На каком примерно расстоянии друг от друга расположены светлые полосы на экране?
| Дано: d = 0, 1 мм, L = 1, 2 м, l = 500 нм, Dх =? |
Решение
Светлые полосы наблюдаются на экране, если
d ×sin a = m ×l, m = 0, 1, 2, ¼,
m - порядок интерференционной полосы.
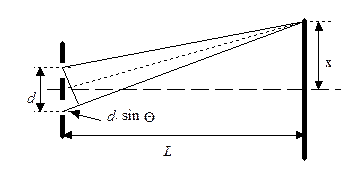
| ||
| Рис. 5 |
Полоса 1-го порядка наблюдается при угле Q1, задаваемом соотношением: sin Q1 = l / d.
Подставив численные значения получим
sin Q1 = 500×10-9м / 10-4м = 5×10-3.
При малом угле можно положить sin Q1» Q1» tg Q1.
Расстояние х1, на котором полоса первого порядка находится от центра экрана, определяется соотношением
х1 / L = Q1 Þ х1 = L × Q1 = 1200 мм × 5×10-3 = 6 мм.
Вторая полоса находится на расстоянии
х2 = L × Q2 = L ×2×l / d = 12 мм, и так далее.
Ответ: Светлые полосы отстоят друг от друга примерно на 6 мм.
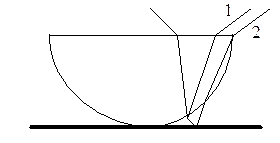
3. Покажите, что радиус r m m - го темного кольца Ньютона при наблюдении по нормали сверху определяется выражением 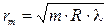 , где R - радиус кривизны поверхности стекла, l - длина волны используемого света. Предполагается, что толщина воздушного зазора всюду намного меньше радиуса кривизны R и что r m много меньше R.
, где R - радиус кривизны поверхности стекла, l - длина волны используемого света. Предполагается, что толщина воздушного зазора всюду намного меньше радиуса кривизны R и что r m много меньше R.
Решение
| 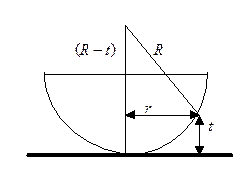
| |||
| Рис. 6 | ||||
Так как при отражении света от среды с большим показателем преломления его фаза меняется на 180°, а при отражении от среды с меньшим показателем преломления его фаза не меняется, луч 1 имеет ту же фазу, что и падающий луч, луч 2 - фазу, отличную от падающего луча на 180°, что означает дополнительную разность хода между лучами 1 и 2, равную l / 2. Тогда условие возникновения темного кольца
2× t + l / 2 = (m + 1/2)×l, m = 0, 1, 2, ¼, или 2× t = l× m,
где t - толщина воздушного зазора между сферической поверхностью и плоской пластинкой. Из геометрии рисунка следует. Что
(R - t)2 + r 2 = R 2
r 2 - 2× t × R + t 2 = 0
так как t << R и t << r, слагаемым t 2 можно пренебречь, и в результате
r 2 = 2× t × R,
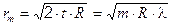 Ответ:
Ответ: 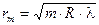
4. Вычислить радиусы первых трех зон Френеля, если расстояние от источника до волновой поверхности равно 1 м, расстояние от волновой поверхности до точки наблюдения также равно 1 м и длина волны света 500 нм.
| Дано: a = 1 м, b = 1 м, l = 500 нм, r 1 =? r 2 =? r 3 =? | 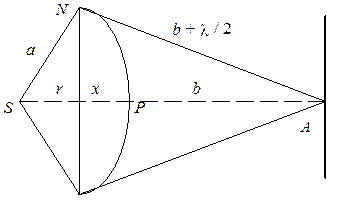
| |
| Рис. 7 |
Найдем радиус 1-й зоны Френеля. Он должен быть таков, чтобы лучи PA и NA, приходящие в точку наблюдения А из центра Р и края N -й зоны Френеля, имели разность хода, равную l / 2.
Обозначим a - расстояние от источника света до сферической волновой поверхности (источник считаем точечным), b - расстояние от волновой поверхности до точки наблюдения. Тогда радиус 1-й зоны Френеля
r 2 = a 2 - (a - x)2 = (b + l / 2)2 - (b + x)2,
Так как l << b, после возведения в квадрат слагаемым l2 / 4 можно пренебречь. В результате получаем уравнение
2× a × x + 2× b × x = b ×l,
откуда 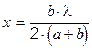 ,
,
и r 2 = a 2 - (a - x)2 = a 2 - a 2 + a×b×l / (a + b)
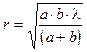 .
.
Аналогично вычисляется радиус m -й зоны Френеля
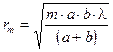 .
.
Ответ: Радиусы первых трех зон Френеля равны
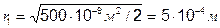 ,
,
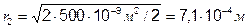 ,
,
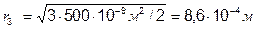
5. Свет с длиной волны 750 нм, падая нормально, проходит через щель шириной 10-3 мм. Какова ширина центрального максимума: а) в градусах; б) в сантиметрах на экране, находящимся на расстоянии 20 см от щели.
| Дано: l = 750 нм, D = 10-3 мм, L = 20 см, 2× х =? 2×Q =? | Решение
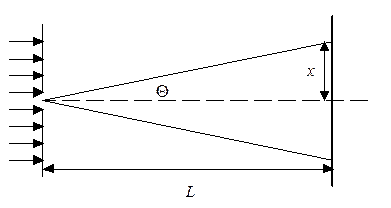
| |
| Рис. 8 |
Ширина щели D настолько мала, что в ней укладывается менее одной зоны Френеля (докажите это самостоятельно). Поэтому в данном случае имеет место дифракция Фраунгофера. На экране наблюдается светящееся изображение щели (центральный максимум), окруженное темными и светлыми полосами (дифракционные минимумы и максимумы).
а) Первый минимум наблюдается под углом Q таким, что
sin Q = l / D.
sin Q = 750×10-9 м / 10-6 м = 0,75 Þ Q = 49°.
б) Ширина центрального максимума равна 2× х.
tg Q = x / L, где L - расстояние до экрана.
2× Х = 2×tg Q× L = 2×tg 49°× 0,2 м = 0,46 м.
Ответ: а) Q = 49°, б) 2× Х = 0,46 м.
6. Желтый свет натрия (которому соответствуют длины волн 589,00 нм и 589,59 нм) падает на дифракционную решетку, имеющую 7500 штрихов / см. Определить: а) максимальный порядок для желтого света натрия; б) ширину решетки, необходимую для разрешения двух линий натрия; в) разрешающую способность дифракционной решетки в этом случае.
| Дано: l1 = 589,00 нм, l2 = 589,59 нм, n = 7500 штрих / см, m =? R =? N =? |
Решение
а) Период дифракционной решетки будет равен d = 1 / n = 1×0,01 м / 7500 = 1,33×10-6м.
Максимальный порядок m может быть найден из условия возникновения максимумов для дифракционной решетки: d × sin Q = m ×l.
Учитывая, что Qmax £ 90° получим: m = (d ×sin Qmax) / l < d / l.
m = 1,33×10-6м / 5,89×10-7м = 2,25.
Округляя это значение до меньшего целого, получаем ответ m = 2.
б) Разрешающая способность решетки определяется выражением
R = l1 / Dl = N × m,
где Dl - разность длин волн близких спектральных линий, разрешаемых решеткой; N - полное число штрихов решетки; m - порядок максимума.
N = D / d,
где D - ширина решетки.
Для разрешения спектральных линий с разностью длин волн Dl решетка должна иметь ширину: D = N × d = d ×l1 / (Dl× m),
Для разрешения линий натрия во втором максимуме решетка должна иметь ширину D = 1,33×10-6м×589×10-9м / (2×0,59×10-9м) = 6,67×10-4м.
в) Разрешающая способность решетки находится из формулы
R = l1 / Dl.
При подстановке численных данных получаем:
R = 589 нм / 0,59 нм = 1000.
Чтобы достичь ее, полное число штрихов должно быть равно:
N = R / m = 1000 / 2 = 500.
Ответ: а) m = 2, б) D = 6,67×10-4м, в) R = 1000, N = 500.
7. Неполяризованный свет проходит через два поляроида. Ось одного вертикальна, а ось другого образует с вертикалью угол Q = 60°. Найти интенсивность прошедшего света.
Решение
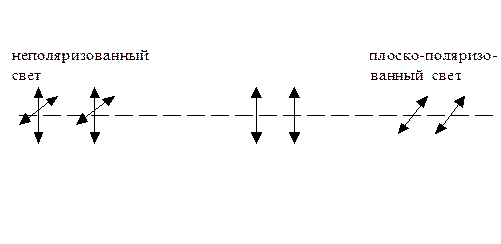
| ||
| Рис. 9 |
Первый поляроид исключает половину света, поэтому после его прохождения интенсивность света уменьшается в два раза:
I 1 = I 0 / 2.
Свет, падающий на второй поляроид, поляризован в вертикальной плоскости, поэтому после прохождения второго поляроида интенсивность света равна: I 2 = I 1×(cos Q)2 = I 0×(cos Q)2 / 2.
Отсюда I 2 = I 0×(cos 60°)2 / 2 = I 0 / 8.
Ответ: интенсивность прошедшего света составляет 1/8 от интенсивности падающего света, а плоскость его поляризации образует с вертикалью угол 60°.
8. При каком угле падения солнечный свет отражается от поверхности озера плоскополяризованным? Чему равен угол преломления?
Решение
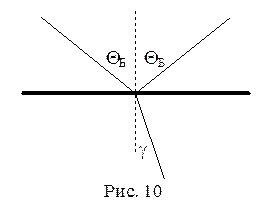
|
Согласно закону Брюстера отраженный луч полностью поляризован, если:
tg QБ = n,
где QБ - угол полной поляризации отраженного от диэлектрика света, n - показатель преломления. Для границы вода-воздух n = 1,33,
отсюда QБ = 33,1°.
При полной поляризации отраженного света выполняется равенство:
QБ + g = 90°
где g - угол преломления.
g = 90° - QБ = 36,9°.
Ответ: g = 36,9°
9. Какую минимальную толщину должна иметь четвертьволновая пластинка кальцита (n0 = 1,658; ne = 1,486) для света с длиной волны 589 нм?
Решение
При распространении луча в кристалле перпендикулярно главной оптической оси между обыкновенным и необыкновенным лучами возникает разность фаз Dj = 2×p ×d× (n o - n e) / l,
где d - толщина кристалла; l - длина волны света.
Четвертьволновой пластинке максимальной толщины соответствует разность фаз Dj = p / 2, или 2×p ×d× (n o - n e) / l = p / 2,
откуда 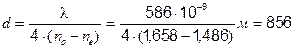 нм.
нм.
Ответ: d = 856 нм
Date: 2015-05-05; view: 2926; Нарушение авторских прав