
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Задание 1.1
|
|
Преобразовать 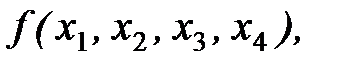 используя формулу дизъюнктивного разложения по совокупности переменных
используя формулу дизъюнктивного разложения по совокупности переменных 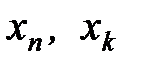 , представляя получаемые функции от двух переменных формулами над множеством элементарных связок: отрицание, конъюнкция, дизъюнкция, импликация, сумма по модулю два, эквиваленция, запрет, штрих Шеффера, стрелка Пирса.
, представляя получаемые функции от двух переменных формулами над множеством элементарных связок: отрицание, конъюнкция, дизъюнкция, импликация, сумма по модулю два, эквиваленция, запрет, штрих Шеффера, стрелка Пирса.
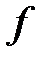
| n | k |
| 0110 1110 1101 1001 |
Решение.
Разложение функции 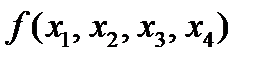 по переменным
по переменным 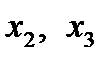 будет выглядеть так:
будет выглядеть так:
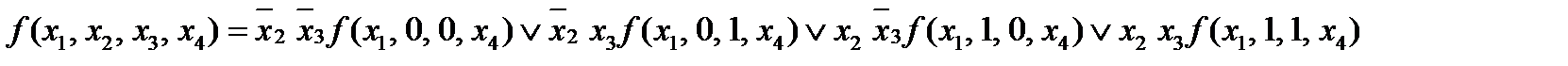
Запишем совершенную ДНФ функции 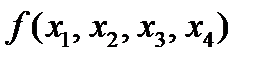 .
.
Для этого сначала запишем таблицу истинности (таблицу состояний) функции 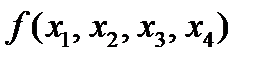 .
.
| x1 | x2 | x3 | x4 | f |
Теперь по таблице запишем СДНФ для данной функции

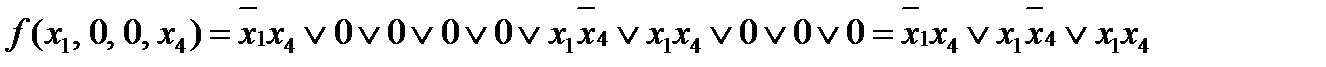
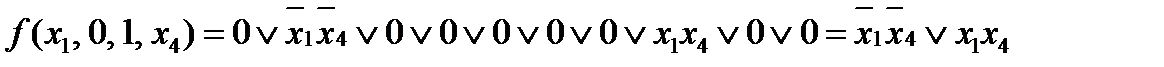
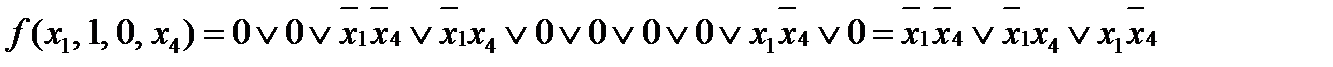
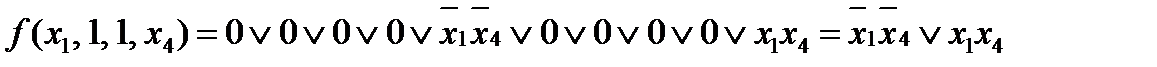
То есть разложение функции 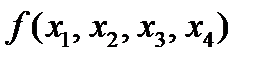 по переменным
по переменным 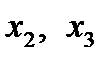 будет выглядеть так:
будет выглядеть так:
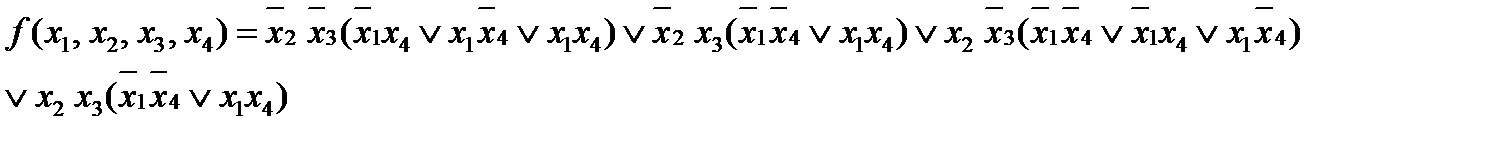
Теперь требуется записать эту форму используя функции: отрицание, конъюнкция, дизъюнкция, импликация, сумма по модулю два, эквиваленция, запрет, штрих Шеффера, стрелка Пирса.
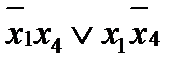 - это представление в базисе «и», «или», «не» логической функции
- это представление в базисе «и», «или», «не» логической функции 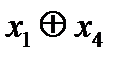 - сумма по модулю два.
- сумма по модулю два.
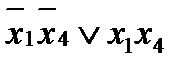 - это представление в базисе «и», «или», «не» логической функции
- это представление в базисе «и», «или», «не» логической функции 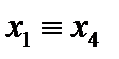 - эквиваленция (равнозначность)
- эквиваленция (равнозначность)
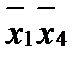 - это представление в базисе «и», «или», «не» логической функции
- это представление в базисе «и», «или», «не» логической функции 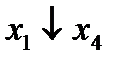 - стрелка Пирса
- стрелка Пирса
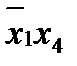 -это представление в базисе «и», «или», «не» логической функции
-это представление в базисе «и», «или», «не» логической функции  - запрет
- запрет 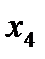
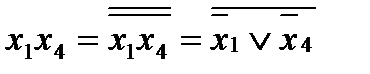
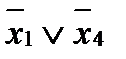 -это представление в базисе «и», «или», «не» логической функции
-это представление в базисе «и», «или», «не» логической функции 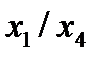 - штрих шеффера
- штрих шеффера
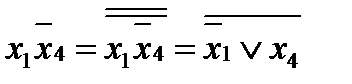
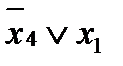 - это представление в базисе «и», «или», «не» логической функции
- это представление в базисе «и», «или», «не» логической функции 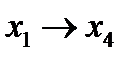 - импликация
- импликация 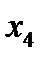
Итак, требуемое представление функции:
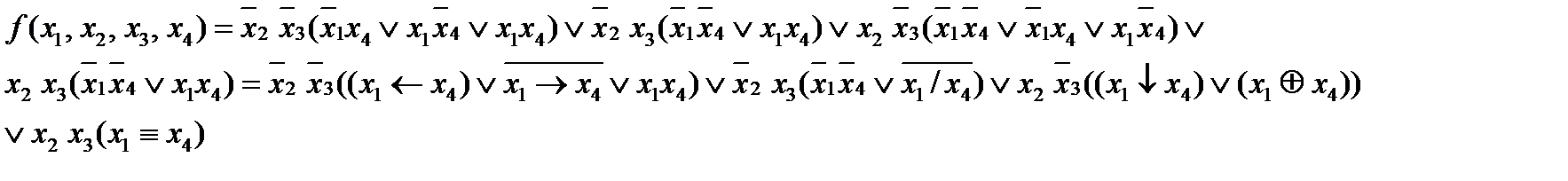
Date: 2015-04-23; view: 4301; Нарушение авторских прав