
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Примеры решения задач по молекулярной физике
|
|
При решении задач этого раздела необходимо пользоваться следующими рекомендациями:
Использовать уравнение состояния идеального газа (уравнение Менделеева-Клапейрона) для определения макро-параметров состояния газа
 . (2.8.1)
. (2.8.1)
2. Для определения микроскопических характеристик молекулярного движения использовать функцию распределения Максвелла молекул по скоростям или функцию распределения Больцмана при наличии потенциальных силовых полей:
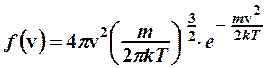 ; (2.8.2)
; (2.8.2)
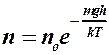 . (2.8.3)
. (2.8.3)
Использовать уравнения переноса, формулы коэффици-ентов переноса (внутреннего трения, диффузии, теплопроводности) и явления столкновения молекул (длина свободного пробега, эффективное сечение молекул).
4. Использовать уравнения кинетической теории газов и закон Дальтона:
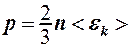 ; (2.8.4)
; (2.8.4)
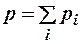 . (2.8.5)
. (2.8.5)
Пример 1. Найти число молекул кислорода, находящегося в объеме V = 2·10- 3 м 3 при температуре Т = 300 К и давлении р = 10 5 Па, скорости которых лежат в интервале от 490 до 500 м/c.
Дано: V = 2·10- 3 м 3 ; Т = 300 К; р = 10 5 Па; 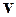 = 490 – 500 м/с.
= 490 – 500 м/с.
 Найти: N -?
Найти: N -?
Решение. Число искомых молекул 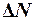 связано с полным числом молекул газа соотношением
связано с полным числом молекул газа соотношением
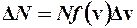 , (1)
, (1)
где 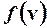 – функция распределения Максвелла (2.8.2),
– функция распределения Максвелла (2.8.2), 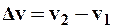 .
.
Аргументом v функции 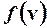 служит среднее арифметическое между v1 и v2, которое можно считать как v = v 2 = 500 м/с в силу малости
служит среднее арифметическое между v1 и v2, которое можно считать как v = v 2 = 500 м/с в силу малости 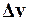 по сравнению с v1 и v2.
по сравнению с v1 и v2.
Число молекул N получим из уравнения состояния идеального газа (2.8.1) для нормальных условий, т.е. при давлении р = 10 5 Па и температуре Т = 273 К:
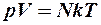 . (2)
. (2)
Учитывая, что 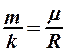 , из формулы (1) найдем
, из формулы (1) найдем
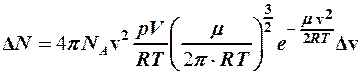 . (3)
. (3)
Подстановка числовых значений в выражение (3) дает
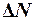 = 1,29·10 22.
= 1,29·10 22.
Ответ: 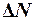 = 1,29·10 22.
= 1,29·10 22.
Пример 2. Идеальный газ нагревают при постоянном давлении. Как изменятся средняя длина свободного пробега 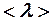 и среднее число столкновений
и среднее число столкновений 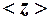 его молекул в одну секунду с изменением температуры?
его молекул в одну секунду с изменением температуры?
 Дано: р = const.
Дано: р = const.
Найти: 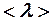 -?,
-?, 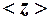 -?
-?
Решение. Если газ нагревать, поддерживая давление посто- янным, то его объем согласно уравнению газового состояния (2.8.1) будет увеличиваться с температурой линейно:
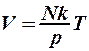 . (1)
. (1)
Концентрация молекул газа будет уменьшаться:
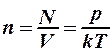 . (2)
. (2)
Длина свободного пробега
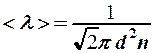 (3)
(3)
зависит только от концентрации (2) и будет расти пропорционально температуре:
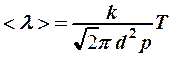 . (4)
. (4)
Частота столкновений с учетом формулы (4)
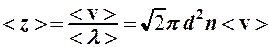 (5)
(5)
зависит от температуры через n исреднеарифметической скорости
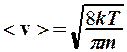 ,
,
т. е. 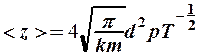 ,
,
и при р = const уменьшается с ростом температуры как  .
.
Ответ: 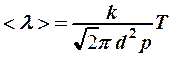 ;
; 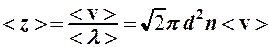 .
.
Задачи
2.98. Найти наиболее вероятную  и среднюю
и среднюю 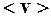 скорости молекул хлора при температуре Т = 500 К. Молярная масса хлора
скорости молекул хлора при температуре Т = 500 К. Молярная масса хлора 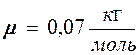 .
.
2.99. На какой высоте давление воздуха р вдвое меньше давления 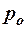 на уровне моря? Температуру Т = 273 К считать постоянной.
на уровне моря? Температуру Т = 273 К считать постоянной.
2.100. Найти число молекул водорода, находящегося в нормальных условиях в объеме V = 10-3 м 3 , скорости которых лежат в интервале от 990 до 1000 м/c.
2.101. Найти кинетическую энергию молекул водорода, находящегося в объеме V = 5 л под давлением р = 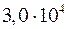 Па.
Па.
2.102. Какова длина свободного  пробега молекул воздуха при давлении p = 100 Па и температуре 17
пробега молекул воздуха при давлении p = 100 Па и температуре 17 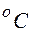 ? Эффективный диаметр молекулы d = 3·10- 10 м.
? Эффективный диаметр молекулы d = 3·10- 10 м.
2.103. Газ при давлении p = 980 ГПа и температуре to = 20 о С имеет объем V = 164 м 3. Каков объем той же массы газа при нормальных условиях?
2.104. При каком давлении р средняя длина свободного пробега молекул азота 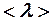 = 1 мм, если при нормальном давлении
= 1 мм, если при нормальном давлении  она равна
она равна 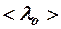 =
=  см?
см?
2.105. Найти коэффициент теплопроводности гелия, составляющего атмосферу Солнца. Температура солнечной поверхности Т = 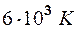 . Эффективный диаметр атомов гелия d = 2,18·10-10 м, молярная масса
. Эффективный диаметр атомов гелия d = 2,18·10-10 м, молярная масса 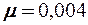 кг/моль.
кг/моль.
2.106. В сосуде объемом V = 5·10- 3 м 3 содержится N = 1023 молекул одноатомного газа. Коэффициент теплопроводности этого газа 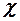 =
= 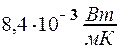 . Найти при этих условиях коэффициент диффузии газа D.
. Найти при этих условиях коэффициент диффузии газа D.
2.107. Вычислить среднюю длину свободного пробега 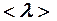 и время
и время 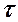 между двумя столкновениями молекул кислорода при давлении р = 0,2 м Па и температуре Т = 290 К. Эффективный диаметр молекул кислорода d =
между двумя столкновениями молекул кислорода при давлении р = 0,2 м Па и температуре Т = 290 К. Эффективный диаметр молекул кислорода d = 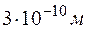 .
.
2.108. Вычислить коэффициент теплопроводности водорода
(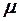 =
= 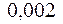 кг/ моль), вязкость которого
кг/ моль), вязкость которого 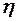 =
= 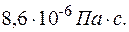
2.109. Во сколько раз изменится коэффициент вязкости воздуха при понижении температуры от t 1 = 20 o C до t 2 = - 40 o C в связи с подъемом самолета на большую высоту?
2.110. Двухатомный газ, масса которого m = 1 кг и плотность
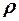 = 4 кг / м 3, находится под давлением р = 80 к Па. Найти энергию
= 4 кг / м 3, находится под давлением р = 80 к Па. Найти энергию
теплового движения W молекул газа при этих условиях.
2.7. Термодинамика
2.1. Укажите, какие ответы могут быть окончанием фразы:
«Термодинамикой называют раздел курса физики, который изучает…
1. …свойства тел и изменений состояния вещества, не интересуясь их микроскопической структурой».
2. …самопроизвольные колебания параметров вблизи их равновесных значений, возникающих при тепловых процессах».
3. …обмен тепловой энергией как между системой, так и с внешней средой и превращение ее в механическую работу».
4. …общие закономерности перехода систем в состояние термодинамического равновесия».
5. …медленные процессы, называемые квазистатическими, которые рассматриваются как непрерывная последовательность практически равновесных состояний».
2.2. Дайте определение термодинамической системы.
1. Система, которая не обменивается энергией с окружающей внешней средой.
2. Система, которая вне зависимости от начального состояния в ней через некоторое конечное время переходит в термодинамическое равновесие.
3. Тело, характеризуемое внутренними и внешними макроскопическими параметрами.
4. Система, состоящая из большого количества частиц, которые могут обмениваться тепловой энергией, как между собой, так и с внешней средой.
5. Правильного ответа нет.
2.3. Что называется равновесным состоянием системы?
1. Состояние системы, в котором все ее параметры изменяются со временем.
2. Состояние системы, при котором все ее параметры имеют определенные значения, остающиеся при неизменных внешних условиях постоянными сколь угодно долго.
3. Состояние системы, при котором параметры системы не изменяются с течением времени и в ней отсутствуют макроскопические потоки вещества и энергиии.
4. Переход системы из одного состояния в другое, который связан с нарушением равновесия.
5. Правильного ответа нет.
2.4. Каков физический смысл понятия «температура»?
1. Степень нагретости тела.
2. Мера внутренней энергии вещества.
3. Мера средней кинетической энергии теплового движения.
4. Мера числа столкновений молекул.
5. Мера агрегатного состояния вещества.
2.5. Какими макроскопическими параметрами описывается состояние газовой термодинамической системы?
1. Массой m, плотностью 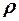 , поляризованностью
, поляризованностью 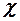 .
.
2. Давлением р, объемом V, температурой T.
3. Намагниченностью J, напряженностью Е, весом тела P.
4. Твердостью R, количеством теплоты Q, молярной массой 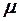 .
.
2.6. Укажите уравнение состояния идеального газа для любой мас- сы газа.
1. pV = RT. 2. pV = 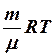 . 3.
. 3. 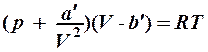 .
.
4. p(V – b) = RT. 5. p 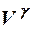
 = const.
= const.
2.7. Укажите формулу средней кинетической энергии молекулы идеального газа для любой массы.
1. 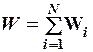 . 2.
. 2. 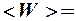
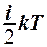 . 3.
. 3. 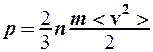 .
.
4. 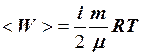 . 5.
. 5. 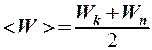 .
.
2.8. Из каких видов энергии состоит внутренняя энергия идеального газа?
1. Из внутримолекулярной энергии частиц.
2. Средней кинетической энергии хаотического движения молекул газа.
3. Средней потенциальной энергии молекул.
4. Энергии взаимодействия атомов и молекул.
2.9. Укажите формулу для вычисления внутренней энергии идеального газа для любой массы m.
1. U = 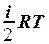 . 2. U = NA
. 2. U = NA 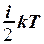 . 3. U =
. 3. U = 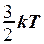 .
.
4. U =  . 5. U =
. 5. U = 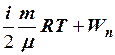 .
.
2.10. По отношению к каким величинам бесконечно малое приращение соответствует полному дифференциалу?
1. Работе. 2. Количеству теплоты. 3. Энтропии.
4. Внутренней энергии. 5. Температуре. 6. Давлению.
2.11. Дайте наиболее полную формулировку первого закона термодинамики.
1. Работа и теплота превращаются друг в друга.
2. Теплота Q и работа A определяют количество энергии, кото- рыми система обменивается с внешними телами в процессах теплообмена и работы.
3. Количество тепла, сообщаемое системе, идет на приращение внутренней энергии системы и совершение системой работы над внешними телами.
4. Работа системы, которая совершает круговой процесс, выпол- няется за счет теплоты, взятой у внешних тел.
5. Невозможен вечный двигатель ”Perpetum mobile” первого рода, который мог бы совершать работу, не заимствуя энергию у внешних тел.
2.12. Для какого из перечисленных процессов выполняется условие Q = A?
1. Адиабатического. 2. Изотермического. 3. Изобарного.
4. Изохорического. 5. Политропического.
2.13. 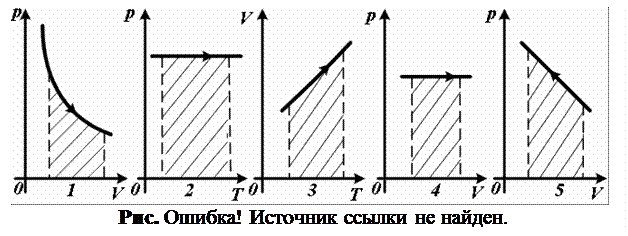
На каком из графиков (рис. 2.13) заштрихованная площадь представляет собой работу газа в изотермическом процессе?
2.14. На каких из графиков (см. рис. 2.13) газовых процессов заштрихованная площадь представляет собой работу газа?
2.15. Работа сжатия газа оказалась равной его изменению внутренней энергии. Какому процессу это соответствует?
1. Адиабатическому. 2. Изохорному. 3. Изотермическому.
4. Изобарному. 5. Политропическому.
2.16. Газ нагревают в герметически закрытом сосуде. Какой из процессов имеет место?
1. Адиабатический. 2. Изотермический. 3. Изохорический.
4. Изобарический. 5. Политропический.
2.17. Какие из выражений соответствуют работе газа?
1. A = p Δ V. 2. A =  . 3. A =
. 3. A = 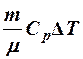 .
.
4. 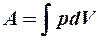 . 5. A =
. 5. A = 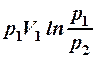 .
.
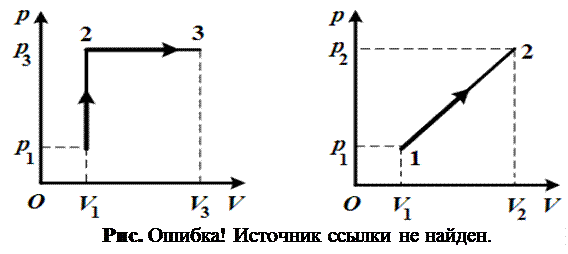
2.18. Найти работу газа А процесса, изображенного на рис. 2.18.
2.19. Найти работу газа А процесса, изображенного на рис. 2.19.
2.20. Какое из уравнений первого закона термодинамики соответствует изотермическому процессу?
1. 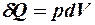 . 2.
. 2. 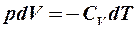 . 3.
. 3. 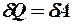 .
.
 |
4.
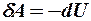 . 5.
. 5. 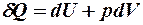 .
.
2.21. Какие из приведенных формул выражают работу изотермического процесса расширения газа?
1. А =  . 2. A =
. 2. A = 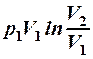 . 3. A =
. 3. A = 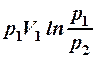 .
.
4. A = 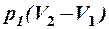 . 5. A =
. 5. A = 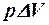 .
.
2.22. Какое из выражений соответствует молярной теплоемкости идеального газа при постоянном давлении?
1. 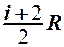 . 2.
. 2. 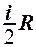 . 3.
. 3. 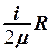 . 4.
. 4. 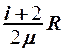 . 5.
. 5. 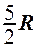 .
.
2.23. Какое из уравнений первого закона термодинамики справедливо для изохорического процесса?
1. 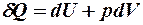 . 2.
. 2. 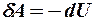 . 3.
. 3. 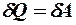 .
.
4. 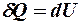 . 5.
. 5. 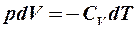 .
.
2.24. Какое из приведенных выражений соответствует молярной теплоемкости идеального газа при постоянном объеме?
1. 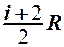 . 2.
. 2. 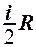 . 3.
. 3. 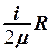 . 4.
. 4. 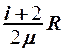 . 5.
. 5. 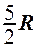 .
.
2.25. Какие из формул определяют первый закон термодинамики для адиабатического процесса?
1. 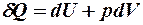 . 2.
. 2. 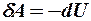 . 3.
. 3. 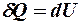 . 4.
. 4. 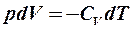 .
.
2.26. Какой из перечисленных процессов называется адиабатическим?
1. Перенос теплоты потоком жидкости или газа.
2. Процесс, при котором теплоемкость постоянна.
3. Передача теплоты от одного тела к другому при их контакте.
4. Процесс, происходящий без теплообмена с окружающей средой.
5. Перенос теплоты с помощью электромагнитных волн.
2.27. Какое из уравнений первого закона термодинамики справедливо для изобарического процесса?
1. 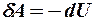 . 2.
. 2. 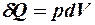 . 3.
. 3. 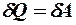 .
.
4. 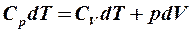 . 5.
. 5. 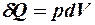 .
.
2.28. Укажите, на какую величину молярная теплоемкость идеального газа при постоянном давлении больше, чем при постоянном объеме.
1. 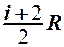 . 2.
. 2. 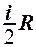 . 3.
. 3. 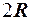 . 4.
. 4. 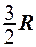 . 5.
. 5. 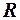 .
.
2.29. Какое из выражений определяет обратимый термодинамический процесс?
1. В системе происходят процессы, в результате которых изменяется состояние.
2. Циклический процесс, в результате которого система возвращается в исходное состояние.
3. Такое изменение состояния системы, при котором она может возвращаться в начальное состояние без остаточных изменений в системе и окружающей среде.
4. Процесс превращения всего количества теплоты, получаемой системой от внешней среды, в работу.
5. Циклический процесс, происходящий по часовой стрелке.
2.30. Какая из кривых прямого цикла Карно (рис. 2.30) соответствует адиабатическому расширению?
2.31. Какая из кривых прямого цикла Карн о (см. рис. 2.30) соответствует изотермическому расширению?
2.32. Чему численно равно количество теплоты, полученной от нагревателя за один прямой цикл Карно (см. рис. 2.30)?
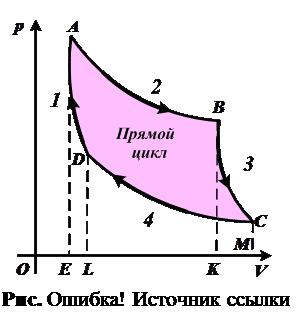 1. Площади EABCM.
1. Площади EABCM.
2. Площади EABK.
3. Площади EADL.
4. Площади ABCD.
5. Площади KBCM.
2.33. Чему численно равна полез- ная работа прямого цикла Карно ( см. рис. 2.30)?
1. Площади EABCM.
2. Площади EABK.
3. Площади EADL.
4. Площади ABCD.
5. Площади KBCM.
2.34. Какая из кривых обратного цикла Карно (рис. 2.34) соответствует адиабатическому сжатию?
2.35. 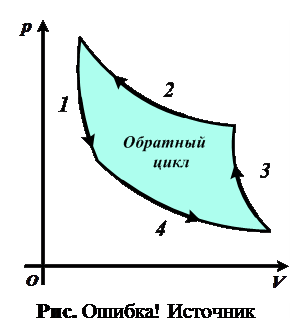 Какая из кривых обратного цикла Карно (см. рис. 2.34) соответствует изотермическому сжатию?
Какая из кривых обратного цикла Карно (см. рис. 2.34) соответствует изотермическому сжатию?
2.36. Укажите определение КПД цикла Карно.
1. Невозможен такой периоди- чески действующий двигатель, который совершал бы работу в большем количестве, чем получаемая им энергия.
2. 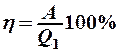 , где А – работа, совершенная за цикл;
, где А – работа, совершенная за цикл; 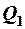 – количество теплоты, переданное от нагревателя.
– количество теплоты, переданное от нагревателя.
3. КПД обратимых машин, работающих с одним и тем же нагревателем и холодильником, должен быть одинаков.
4. Отношение разности температур нагревателя и холодильника к температуре нагревателя, т. е.
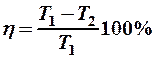 .
.
2.37. Какие характеристики являются функциями состояния вещества?
1. Внутренняя энергия. 2. Выполненная работа.
3. Количество теплоты. 4. Энтропия. 5. Правильного ответа нет.
2.38. Какие свойства вещества характеризует энтропия?
1. Степень превращаемости теплоты в работу.
2. Температуру тела.
3. Степень неупорядоченности движения молекул.
4. Внутреннюю энергию. 5. Правильного ответа нет.
2.39. Укажите формулировки второго закона термодинамики.
1. Внутренняя энергия непосредственно и полностью не превращается в механическую работу.
2. Теплота не может переходить сама по себе от тела с низкой температурой к телу с более высокой температурой.
3. Невозможен процесс, единственным результатом которого является превращение всей теплоты в эквивалентную ей работу.
4. ”Perpetum mobile” второго рода создать невозможно.
5. При самопроизвольном процессе тепло переходит от более нагретого тела к менее нагретому телу.
2.40. Укажите математическое выражение записи второго закона термодинамики.
1. 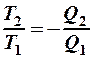 . 2.
. 2.  . 3.
. 3. 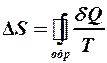 .
.
4. 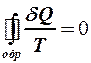 . 5.
. 5.  .
.
2.41. Какая формула связывает энтропию с термодинамической вероятностью состояния?
1. 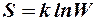 . 2.
. 2. 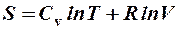 . 3.
. 3. 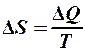 .
.
4. 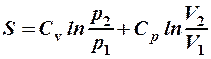 . 5.
. 5. 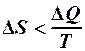 .
.
2.42. Какому из перечисленных условий удовлетворяет обратимый процесс в изолированной системе?
1. Энтропия системы остается неизменной.
2. Энтропия системы уменьшается.
3. Энтропия системы увеличивается.
4. Энтропия системы увеличивается, а затем уменьшается.
5. Энтропия системы уменьшается, а затем увеличивается.
2.43. Укажите основные задачи термодинамики.
1. Определение изменения внутренней энергии системы, если известны начальное и конечное ее состояния.
2. Вычисление работы, совершаемой системой, и количества теплоты, полученной (или отданной) ею, если известны промежуточные состояния (т.е. известен процесс).
3. Нахождение макроскопических параметров состояния системы при переходе ее из одного состояния в другое.
4. Применение закона сохранения энергии для изолированных термодинамических систем.
5. Определение небольшим количеством макроскопических параметров (давление p, объем V, температура T и некоторые другие) равновесного состояния системы, состоящей из большого числа частиц.
Date: 2015-05-05; view: 3601; Нарушение авторских прав