
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

A1: e 1 8 f
|
|
a2: E 2 F 5
a3: 2 0 E 8
a4 :5 3 E 2
3. Запишем адрес первого числа как <seg>:<offset> в виде второго числа:
1E8F: E2F5.
Адрес второго числа получается увеличением на 2 адреса первого числа:
1E8F: E2F7.
Вычислим физический адрес памяти размещения первого и второго числа, используя формулу <физ. адрес> = <seg>*p + <offset>, где p=10H.
Физический адрес:
-первого числа равен 1E8F0 + E2F5 = 2CB65.
-второго числа равен 1E8F0 + E2F7 = 2CB67.
Покажем размещение чисел в памяти компьютера: при записи чисел в память следует помнить, что система хранит в памяти байты слова в обратной последовательности: младшая часть по меньшему адресу, а старшая - по большему адресу.
| ADR | DATA |
| 2CB65 | E8 |
| 2CB66 | |
| 2CB67 | E2 |
| 2CB68 |
3. Переведем данные числа в десятеричную систему счисления по формуле 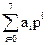 , где p – основание исходной системы счисления, в нашем случае мы переводим из шестнадцатеричной системы счисления т.е. р=16, ai – цифра исходного числа.
, где p – основание исходной системы счисления, в нашем случае мы переводим из шестнадцатеричной системы счисления т.е. р=16, ai – цифра исходного числа.
Переведём первое число:
a1 = E18FН = 15*160 + 8*161 + 1*162 + 14*163 = 57344
Переведём второе число:
a2 = E2F5Н = 5*160 + 15*161 + 2*162 + 14*163 =17141
Переведём третье число:
a3 = 20E8Н= 8*160 + 14*161 + 0*162 + 2*163 = 744
Переведём четвертое число:
a4 :53E2 = 2*160 + 3*161 + 14*162 + 5*163 =21474
4. Переведем полученные шестнадцатеричные числа в двоичную систему счисления, сопоставив каждой цифре H-кода 4 цифры двоичного кода.
Переведём первое число a1:
F = 1111; 8 = 1000;1 = 0001; E = 1110
Получаем E18FН = 111 0000 11000 1111В
Переведём второе число a2:
5= 0101; F = 1111; 26 = 0010; E = 1110
Получаем E2F516 = 1110 0010 1111 0101В
Переведём третье число a3:
20E8Н =0010 0000 1110 1000В
Переведём четвертое число a4:
52E2H = 0101 0010 1110 0010B
АРИФМЕТИЧЕСКИЕ ОПЕРАЦИИ С ДВОИЧНЫМИ ЧИСЛАМИ СО ЗНАКОМ
1. Для последующих арифметических операций образуем из исходных чисел двоичные числа A и B с нулевым старшим битом. Заменим в исходном первом числе и втором числе старший бит на нуль.
Преобразуя числа получим:
число A = 0 110 0001 1000 1111
число B = 0 110 0010 1111 0101
2. Выполним действия сложения (вычитания) двоичных чисел при всех возможных сочетаниях знаков слагаемых, для этого представим числа –А и –В в дополнительном коде, используя правило:
Aдоп = Аобр+1, если число отрицательное
Сложение двоичных чисел А+В
0 110 0001 1000 1111
+
0 110 0010 1111 0101
1 100 0100 1000 0100
При сложении двух положительных чисел сумма - отрицательное число (в знаковом разряде 1).
Мы получили неверный результат при сложении. Это произошло из-за переполнения разрядной сетки АЛУ, возникшего при выполнении действия A+B. Чтобы избежать переполнения, нужно увеличить разрядность АЛУ, т.е. каждое из положительных чисел дополнить нулем слева.
а1 =0 0110 0001 1000 1111
+
а2 =0 0110 0010 1111 0101
0 1100 0100 1000 0100
Проверка:
Проверим правильность полученных результатов, выполнив действия сложения чисел а1 и а2 в десятичной системе счисления:
а1 = 2497510
а2 = 2533310
Выполним действие а1+а2 = 24975 + 25333 = 50308.
Результат переведём в двоичную систему счисления и запишем его в дополнительном коде:
5039810 =0 0000 1100 0100 1000 0100
Данный результат сложения чисел +а1 и +а2 в дополнительном коде совпал с результатом сложения этих же чисел в десятичной системе счисления, произведённым выше.
После корректировки разрядности АЛУ получаем представление чисел в дополнительном коде:
А = 0 0110 0001 1000 1111
В = 0 0110 0010 1111 0101
Адоп = 1 1001 1110 0111 0001
Вдоп = 1 1001 1101 0000 1011
Вычитание А–В= А+ Вдоп
0 0110 0001 1000 1111
+
1 1001 1101 0000 1011
1 1111 1110 1001 1010
Проверка:
Проверим правильность полученного результата, выполнив действия сложения чисел А и – В в десятичной системе счисления.
Выполним действие А–В = 24975 – 25333 = -- 358.
Результат переведём в двоичную систему счисления и запишем его в дополнительном коде:
-35810 =1 0000 0001 0110 0110
Аобр = 1111 1110 1001 1001
+ 1
Адоп = 1 1111 1110 1001 1010
Данный результат совпал с дополнительным кодом разности чисел +а1–а2, полученным раннее. Знаковый разряд (1) указывает на то, что результат вычитания отрицательный.
Вычитание В–А = В+Адоп
0 0110 0010 1111 0101
+
1 1001 1110 0111 0001
0 0000 0001 0110 0110
Проверка:
Проверим правильность полученного результата, выполнив сложения чисел В – А в десятичной системе счисления.
Выполним действие -А+В = -24975 + 25333 = + 358
Результат переведём в двоичную систему счисления и запишем его в дополнительном коде:
+ 358 = 0 101100110
Данный результат совпал с дополнительным кодом разности чисел +а2–а1, полученным раннее.
Вычитание –А–В = Адоп+Вдоп
1 1001 1110 0111 0001
+
1 1001 1101 0000 1011
(1)1 0011 1011 0111 1100
Проверка:
Проверим правильность полученного результата, выполнив действия сложения чисел – В и – А в десятичной системе счисления/
Выполним действие –В–А= -24975 - 25333 = – 50308.
Результат переведём в двоичную систему счисления и запишем его в дополнительном коде:
–50308= 1 1100 0100 1000 0100
Aобр 0011 1011 0111 1011
Адоп 1 0011 1011 0111 1100
Результат сложения чисел –А и –В в дополнительном коде совпал с дополнительным кодом суммы этих же чисел в десятеричной системе счисления, произведённым выше.
ДЕСЯТИЧНЫЙ ФОРМАТ
Представить значения положительных и отрицательных десятичных чисел А = 24975, В = 25333,─А= 75025, ─ В = 74667 в упакованном и неупакованном BCD.
Date: 2015-05-05; view: 563; Нарушение авторских прав