Площадь плоских фигур

Геометрический смысл определенного интеграла

Пусть f(x), заданная на [a,b], непрерывна и нужно определить площадь, ограниченную кривой y = f(x) и прямыми х = а, х = b, y = 0.

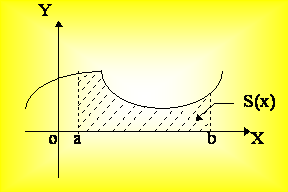
Рис. 4.1

Рис. 4.2

S_i(x) = f(x_i)×Dx_i, где Dх_i = х_i - х_i-1.

.

.

.

.

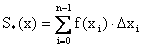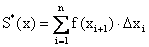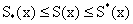Устремим n ® ¥, Dx_i ® 0. Возьмем

.

.

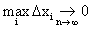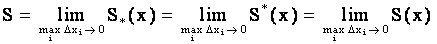Но тогда

.

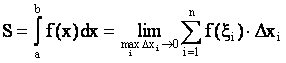Таким образом, определенный интеграл от непрерывной неотрицательной функции при a £ b равен площади соответствующей криволинейной трапеции.

Площадь плоских фигур

Рассмотрим приложения определенного интеграла для вычисления площадей некоторых плоских областей.

Пусть требуется определить S - площадь криволинейной трапеции, ограниченной графиком функции y = f(x), отрезком a £ x £ b и x = a, x = b на основании геометрического смысла определенного интеграла

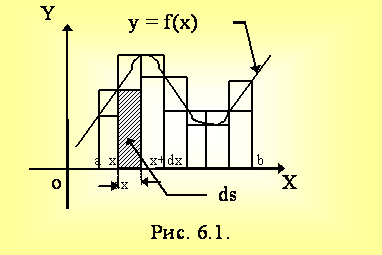
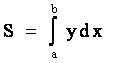, (6.1)

где y = f(х).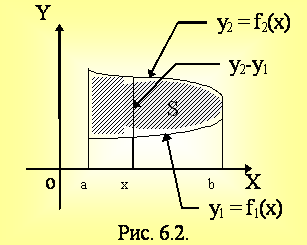

Пусть y₁ = f₁(x), y₂ = f₂(x) (y₂ ³ y₁), x = a, x = b. f₁(x), f₂(x) ³ 0 приxÎ[a,b].

Тогда .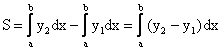

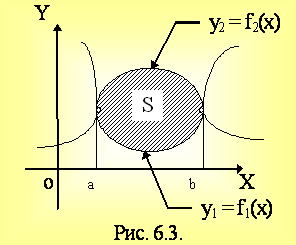
Если f₁(x) = y₁, f₂(x) = y₂

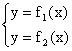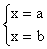; - решение системы. Тогда так же имеем

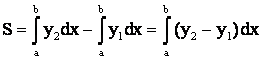. (6.2)

Date: 2015-06-08; view: 564; Нарушение авторских прав