Глава 3. Статистические распределения

Коллоквиум по курсу

«Статистическая физика в биологических системах»

Каф. «Медицинская физика» ИФНИТ 4 курс, гр. 43431/1, 43431/3

КОЛЛОКВИУМ

Тема 1. Математический аппарат статистической физики

1.Элемент объема в декартовой системе координат.

2.Элемент объема в цилиндрической системе координат.

3.Элемент объема в сферической системе координат.

4. Определение якобиана.

5. Якобиан перехода от декартовой системы координат к цилиндрической системе координат

6. Якобиан перехода от декартовой системы координат к сферической системе координат

7. Значения гамма функции для целых значений аргумента.

8. Значения гамма функции для дробных значений аргумента.

9. Значение интеграла в полубесконечных пределах от произведения любой степенной функции на экспоненциальную функцию со сложным степенным аргументом.

10. Нормированное гауссовское распределение. Понятие среднего. Дисперсия. Среднеквадратичное отклонение.

11. Распределение Максвелла по импульсам для частиц в идеальном максвелловском газе.

12. Распределение Максвелла по энергии частиц в максвелловском газе.

13. Средняя скорость частицы в максвелловском газе.

14. Наиболее вероятная скорость частицы в максвелловском газе.

15. Средняя энергия, приходящаяся на одну частицу в максвелловском газе.

16. Число ударов о стенку идеального газа.

17. Давление идеального газа и связь его с температурой.

18. Частота столкновений молекул между собой в максвелловском газе.

КОЛЛОКВИУМ

Тема 2. Основные понятия статистической физики

1. Дифференциал вероятности того, что при наблюдении подсистемы в некоторый произвольный момент времени, она находится с координатами, находящимися в интервале [q]→ [q]+[dq], [p]→ [p]+[dp]. Понятие функции статистического распределения.

2. Среднее значение величины в статистической физике, вычисляемое по известной функции распределения .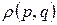

3. Теорема Лиувилля.

4. Относительная флуктуация величины 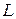для системы, состоящей из 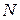независимых частей, в зависимости от величины .

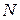5. Выражение для среднего значения физической величины 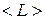через шпур, в котором фигурирует статистический оператор (матрица плотности) и оператор физической величины .

6. Уравнение для статистического оператора (матрицы плотности).

7. Определение бозонов.

8. Определение фермионов.

9. Свойство многочастичной волновой функции бозонов относительно перестановки двух бозонов.

10. Свойство многочастичной волновой функции фермионов относительно перестановки двух фермионов.

11. Действие операторов уничтожения 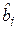и рождения бозонов на волновую функцию бозонов в представлении чисел заполнения.

12. Коммутационные соотношения между операторами уничтожения 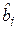и рождения бозонов.

13. Гамильтониан системы 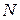невзаимодействующих бозонов в представлении вторичного квантования.

14. Многочастичная функция системы фермионов, построенная на одночастичных функциях фермионов.

15. Формулировка принципа Паули.

16. Действие операторов уничтожения 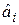и рождения 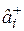фермионов на волновую функцию фермионов в представлении чисел заполнения.

17. Коммутационные соотношения между операторами уничтожения 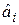и рождения 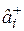фермионов.

18. Гамильтониан системы N невзаимодействующих фермионов в представлении вторичного квантования.

Глава 3. Статистические распределения

19. Зависимость числа состояний 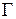от энергии 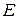для идеального газа, состоящего из 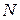частиц.

20. Зависимость плотности состояний 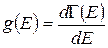от энергии 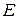для идеального газа, состоящего из 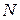частиц.

21. Плотность состояний 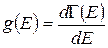для электрона с учетом спинового вырождения фермионов. Переход от суммирования по энергетическим состояниям к интегрированию по энергии.

22. Микроканоническое распределение. Вид равновесной функции распределения для изолированной системы.

23. Каноническое распределение Гиббса для функции распределения 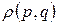, описывающей распределение состояний рассматриваемой выделенной подсистемы, имеющей функцию Гамильтона 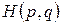и окруженной термостатом, имеющим температуру 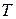. Подсистема обменивается энергией с термостатом.

24. Вид канонического распределения для функции распределения 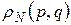, описывающей распределение состояний рассматриваемой выделенной подсистемы, имеющей функцию Гамильтона 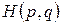и окруженной термостатом, имеющим температуру 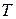. Подсистема обменивается энергией и частицами 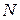с термостатом.

25. Функция распределения Бозе–Эйнштейна для системы бозонов.

26. Функция распределения Ферми–Дирака для системы фермионов.

27. Выражение для концентрации электронов в металле через фермиевский волновой вектор . Случай нулевых температур .

28. Определение интегралов Ферми .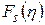

29. Связь концентрации , температуры 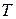, и химического потенциала для электронного газа произвольной степени вырождения.

30. Асимптотика интегралов Ферми для классической (максвелловской статистики) в случае μ<0, .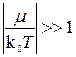

31. Критерий применимости максвелловской статистики.

32. Средняя энергия, приходящаяся на одну частицу в максвелловском газе.

33. Асимптотика интегралов Ферми для вырожденной статистики электронного газа в металлах.

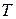34. Зависимость химического потенциала от температуры в вырожденном газе.

////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////