
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

М-теория. Всеобщее увлечение струнной теорией, имевшее место в 1984 году, не могло продолжаться вечно
|
|
Всеобщее увлечение струнной теорией, имевшее место в 1984 году,
не могло продолжаться вечно. К середине 1990-х годов триумфальное
шествие теории суперструн начало сбавлять темп. Легкие проблемы,
которые решала эта теория, были уже все выбраны, и остались только
сложные. Одной из таких проблем было открытие миллиардов реше-
ний струнных уравнений. При компактификации, или свертывании
пространства-времени различным образом, струнные решения
можно было записывать в любом измерении, а не только в четырех.
Каждое из миллиардов струнных решений соответствовало матема-
тически непротиворечивой Вселенной.
Физики внезапно начали тонуть в струнных решениях. Что при-
мечательно, многие из этих решений выглядели очень похожими
на нашу Вселенную. Выбрав подходящее пространство Калаби-Яу,
можно было относительно несложно воспроизвести многие из
существенных черт Стандартной модели с ее причудливым скопле-
нием кварков и лептонов, даже с ее любопытным набором поколе-
ний. Однако чрезвычайно сложной задачей (неразрешенной и по
сей день) было обнаружить первоначальную Стандартную модель
с определенными значениями ее девятнадцати параметров и тремя
излишними поколениями. (Ошеломляющее количество струнных
решений, вообще-то, приветствовалось физиками, которые поддер-
живали идею Мультивселенной, поскольку каждое решение пред-
ставляет полностью непротиворечивую параллельную вселенную.
Однако удручал тот факт, что физики испытывали сложности в обна-
ружении именно нашей Вселенной в этих джунглях вселенных.)
Одной из причин сложности этого предприятия является то, что в
конечном счете суперсимметрию все же нужно разрушить, посколь-
ку в нашем мире низких энергий мы этой симметрии не наблюдаем.
К примеру, мы не видим в природе сэлектрона — суперпартнера
электрона. Если оставить суперсимметрию нетронутой, то масса
каждой частицы должна быть эквивалентна массе ее суперчастицы.
Физики считают, что суперсимметрия была нарушена, и результатом
этого является то, что массы суперчастиц огромны и, таким образом,
суперчастицы находятся вне пределов досягаемости современных
ускорителей частиц. Но в настоящее время никто еще не предложил
правдоподобного механизма для нарушения суперсимметрии.
Дэвид Гросс из Института теоретической физики Кавли в Санта-
Барбаре заметил, что существуют миллионы и миллионы решений
струнной теории в трех пространственных измерениях, что несколь-
ко смущает, поскольку нет способа, с помощью которого мы можем
выбирать среди них.
Были и другие вопросы, в частности то, что существовало пять
непротиворечивых струнных теорий. Было сложно представить, что
Вселенная могла позволять существование пяти отдельных единых
теорий поля. Эйнштейн считал, что у Бога не было выбора при соз-
дании Вселенной, так почему же Бог должен был создать целых пять
вселенных?
Первоначальная теория, основанная на формуле Венециано,
описывает то, что называют суперструнной теорией типа I. В теории
типа I фигурируют как открытые струны (с двумя концами), так и
замкнутые струны (свернутые в окружность). Эту теорию очень
активно разрабатывали в начале 1970-х годов. (Используя струнную
теорию поля, Киккаве и мне удалось каталогизировать полный набор
струнных взаимодействий типа I. Мы показали, что струны типа I
требуют пять взаимодействий. Что касается замкнутых струн, то мы
показали, что там необходим только один член взаимодействия.)
Мы с Киккавой также показали, что возможно построение пол-
ностью непротиворечивых теорий только с замкнутыми струнами
(то есть похожими на петлю). Сегодня такие теории называются
струнными теориями типа II, где струны взаимодействуют путем
расщепления на две струны меньшего размера (этот процесс напо-
минает митоз в клетках).
Наиболее реалистичной струнной теорией считается теория гете-
ротических струн, сформулированная группой ученых из Принстона
(в том числе Дэвидом Гроссом, Эмилем Мартинеком, Райаном Ромом
и Джеффри Харви). Теория гетеротических струн может содержать в
себе группы симметрии, называемые Е(8)хЕ(8) или 0(32), которые
достаточно велики, чтобы включить в себя теории'ТВО. Теория гете-
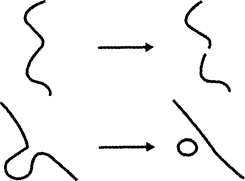
Взаимодействие струн типа I может проходить в пяти различных вариантах. В ходе этих взаимодействий струны могут разрываться, соединяться и расщепляться. Для замкнутых струн характерно лишь последнее взаимодействие, которое напоминает процесс митоза в клетках.
ротических струн полностью основывается на замкнутых струнах.
В 1980-е и 1990-е годы, говоря о теории суперструн, ученые подра-
зумевали теорию гетеротических струн, поскольку она достаточно
богата, чтобы позволить анализировать внутри нее Стандартную мо-
дель и теории ТВО. Например, группу симметрии Е(8)хЕ(8) можно
разбить до симметрии Е(8), а затем — Е(6), которая, в свою очередь,
достаточно велика, чтобы включать симметрию SU(3)xSU(2)xU(l)
«Стандартной модели.
Date: 2015-06-06; view: 505; Нарушение авторских прав