Формула Бернулли. Практические задачи, связанные с оценкой вероятности наступления события в результате нескольких равноценных попыток могут анализироваться с применением

Практические задачи, связанные с оценкой вероятности наступления события в результате нескольких равноценных попыток могут анализироваться с применением формулы Бернулли или (при большом количестве таких попыток) с применением приближенной формулы Пуассона. Для работы с этим материалом Вам снова потребуется знание основ комбинаторики (Раздел 1.2).

Схема Бернулли состоит в следующем: производится последовательность испытаний, в каждом из которых вероятность наступления определенного события А одна и та же и равна р. Испытания предполагаются независимыми (т.е. считается, что вероятность появления события А в каждом из испытаний не зависит от того, появилось или не появилось это событие в других испытаниях). Наступление события А обычно называют успехом, а ненаступление - неудачей. Обозначим вероятность неудачи q=1-P(A)=(1-p). Вероятность того, что в n независимых испытаниях успех наступит ровно m раз, выражается формулой Бернулли:

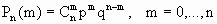
Вероятность Р_n(m) при данном n сначала увеличивается при увеличении m от 0 до некоторого значения m₀, а затем уменьшается при изменении m от m₀ до n.
Поэтому m₀, называют наивероятнейшим числом наступлений успеха в опытах. Это число m₀, заключено между числами np-q и np+p (или, что то же самое, между числами n(p+1)-1 и n(p+1)).Если число np-q - целое число, то наивероятнейших чисел два: np-q и np+p.

Важное замечание. Если np-q< 0, то наивероятнейшее число выигрышей равно нулю.

Пример. Игральная кость бросается 4 раза. При каждом броске нас интересует событие А={выпала шестерка}.

Решение: Здесь четыре испытания, и т.к. кубик симметричен, то

p=P(A)=1/6, q=1-p=5/6.

Вероятность того, что в 4 независимых испытаниях успех наступит ровно m раз (m < 4), выражается формулой Бернулли:

Посчитаем эти значения и запишем их в таблицу.

Самое вероятное число успехов в нашем случае m₀=0.

Пример. Вероятность появления успеха равна 3/5. Найти наивероятнейшее число наступлений успеха, если число испытаний равно 19, 20.

Решение: при n =19 находим

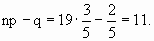
Таким образом, максимальная вероятность достигается для двух значений m₀, равных 11 и 12. Эта вероятность равна P₁₉(11)=P₁₉(12)=0,1797. При n=20 максимальная вероятность достигается только для одного значения m₀, т.к.

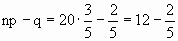
не является целым числом. Наивероятнейшее число наступлений успеха m₀ равно 12. Вероятность его появления равна P₂₀(12)=0,1797. Совпадение чисел P₂₀(12) и P₁₉(12) вызвано лишь сочетанием значений n и p и не имеет общего характера.

На практике в случае, когда n велико, а p мало (обычно p < 0,1; npq < 10) вместо формулы Бернулли применяют приближенную формулу Пуассона

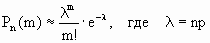
Пример 4. Радиоаппаратура состоит из 1000 элементов. Вероятность отказа одного элемента в течение года равна 0,002. Какова вероятность отказа двух элементов за год? Какова вероятность отказа не менее двух элементов за год?

Решение: будем рассматривать работу каждого элемента как отдельное испытание. Обозначим А={отказ элемента за год}.

P(A)=p=0,002,

l=np=1000*0,002=2<br>
По формуле Пуассона

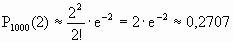
Обозначим через P1000(> 2) вероятность отказа не менее двух элементов за год.
Переходя к противоположному событию, вычислим P1000(> 2) как:

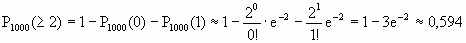
Задачи для самопроверки

1. В семье пять детей. Считая вероятность рождения мальчика и девочки равными 1/2, определить вероятность того, что среди этих детей два мальчика.

2. Наладчик обслуживает 50 станков. Вероятность того, что в течение смены станок потребует регулировки, равна 1/3. Что более вероятно: а) регулировки потребуют 17 станков; б) регулировки потребуют 16 станков?

3. Какова вероятность того, что среди 500 наугад выбранных человек двое родились 1 апреля?

4. Среди 2000 человек приблизительно 16 левшей. Какова вероятность того, что среди сотни наугад выбранных человек окажется хотя бы один левша?

Date: 2015-06-06; view: 614; Нарушение авторских прав