
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Задание 3
|
|
Задания на контрольную работу по дисциплине
«МАТЕМАТИКА»
Для студентов ЗФО
направление 43.03.01«Сервис»
Курс 2 семестр
Учебный год
Контрольная работа №2
Раздел1. Дифференциальные уравнения
ЗАДАНИЕ 1.
Найти решения дифференциальных уравнений первого порядка, удовлетворяющие указанным начальным условиям
1. 3x + xy 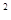 +
+ 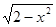 y
y  = 0, y(1) = 1.
= 0, y(1) = 1. 
2. xyy  + x
+ x  e
e 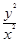 - y
- y 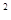 = 0, y(1) = 1.
= 0, y(1) = 1.
3. xdx + ydy = 5x 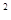 ydy - 10 xy
ydy - 10 xy 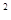 dx, y(1) = 1.
dx, y(1) = 1.
4. xy  = y - y ln (y/x), y(1) = 1.
= y - y ln (y/x), y(1) = 1.
5. (xy 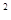 + x) dx +
+ x) dx + 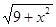 dy = 0, y(0) = 0.
dy = 0, y(0) = 0.
6. y  + 2xy = x e
+ 2xy = x e 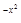 , y(0) = 1.
, y(0) = 1.
7. xy  + y = y
+ y = y 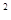 , y(1) = 2.
, y(1) = 2.
8. xy  = y - x tg
= y - x tg 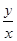 , y(1) =
, y(1) = 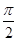 .
.
9. (1 + x 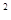 )y
)y  - 2xy = (1 + x
- 2xy = (1 + x 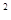 )
) 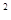 , y(0) = 1.
, y(0) = 1.
10. xy  + y = e
+ y = e 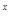 , y(0) = 1.
, y(0) = 1.
ЗАДАНИЕ 2.
Решить дифференциальные уравнения второго порядка: а) найти общее решение; б) найти решение, удовлетворяющее указанным начальным условиям.
1. а) xy  + y
+ y  = x
= x 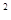 .
.
б) y  - 3y
- 3y  = e
= e 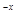 , y(0) = -2, y
, y(0) = -2, y  (0) = 1.
(0) = 1.
2. а) 2yy  - (y
- (y  )
) 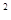 = 0.
= 0.
б) y  - 3y
- 3y  + 2y = x – 1, y(0) = 1, y
+ 2y = x – 1, y(0) = 1, y  (0) = 0.
(0) = 0.
3. а) y  - y
- y  ctg x = sin x.
ctg x = sin x.
б) y  - 6y
- 6y  + 9y = 5sin 3x, y(0) = 0, y
+ 9y = 5sin 3x, y(0) = 0, y  (0) = -1.
(0) = -1.
4. а) y  ctg y - 2(y
ctg y - 2(y  )
) 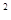 = 0.
= 0.
б) y  + 2y
+ 2y  + 10y = x
+ 10y = x 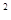 , y(0) = -1, y
, y(0) = -1, y  (0) = 0.
(0) = 0.
5. а) y  ctg x - y
ctg x - y  + 2 = 0.
+ 2 = 0.
б) y  + 4y = 2e
+ 4y = 2e 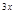 , y(0) = 3, y
, y(0) = 3, y  (0) = 0.
(0) = 0.
6. а) 2y  y
y  y = 1 +(y
y = 1 +(y  )
) 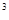 .
.
б) y  - 9y = -2cos x, y(0) = 1, y
- 9y = -2cos x, y(0) = 1, y  (0) = -1.
(0) = -1.
7. а) x y  - y
- y  = y
= y  ln
ln 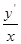 .
.
б) y  - 4y
- 4y  + 5y = 2x – 3, y(0) = 2, y
+ 5y = 2x – 3, y(0) = 2, y  (0) = 0.
(0) = 0.
8. а) (1 – y)y  + 3(y
+ 3(y  )
) 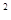 = 0.
= 0.
б) y  - 4y
- 4y  + 3y = e
+ 3y = e 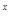 , y(0) = 0, y
, y(0) = 0, y  (0) = 2.
(0) = 2.
9. а) xy  - (y
- (y  )
) 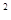 = 0.
= 0.
б) y  - 2y
- 2y  = x + 3, y(0) = 1, y
= x + 3, y(0) = 1, y  (0) = 0.
(0) = 0.
10. а) (y + 1)y  - 3(y
- 3(y  )
) 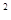 = 0.
= 0.
б) y  - 2y
- 2y  + 2y = cos x, y(0) = 0, y
+ 2y = cos x, y(0) = 0, y  (0) = 0.
(0) = 0.
Раздел 2. Теория вероятностей
ЗАДАНИЕ 3.
1. Стрелок производит восемь выстрелов по мишени, состоящей из центральной части, за попадание в которую он получает 2 очка, и остальной части, за попадание в которую стрелок получает 1 очко. Определить вероятность того, что стрелок наберет 14 очков, если вероятность попадания в центральную часть круга равна 0,1, а в остальную часть — 0,3.
2. Событие 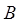 наступает в том случае, если событие
наступает в том случае, если событие 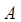 появится не менее трех раз. Определить вероятность появления события
появится не менее трех раз. Определить вероятность появления события 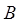 , если вероятность события
, если вероятность события 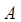 в каждом опыте равна 0,35, и произведено 5 независимых опытов.
в каждом опыте равна 0,35, и произведено 5 независимых опытов.
3. Найти дисперсию дискретной случайной величины 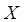 – числа появлений события
– числа появлений события 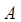 в пяти независимых испытаниях, если вероятность появления события
в пяти независимых испытаниях, если вероятность появления события 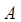 в каждом испытании равна 0,3.
в каждом испытании равна 0,3.
4. Характеристика материала, из которого изготовлена продукция, с вероятностями 0,09; 0,16; 0,25; 0,25; 0,16 и 0,09 может находиться в шести различных интервалах. В зависимости от свойств материала вероятности получения первосортной продукции равны соответственно 0,2; 0,3; 0,4; 0,4; 0,3 и 0,2. Определить вероятность получения первосортной продукции.
5. Имеется 5 урн следующего состава: две урны состава 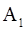 — по 1 белому и 4 черных шара; одна урна состава
— по 1 белому и 4 черных шара; одна урна состава 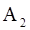 — 2 белых и 3 черных шара; две урны состава
— 2 белых и 3 черных шара; две урны состава 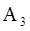 — по 3 белых и 2 черных шара. Из одной наудачу выбранной урны взят шар, он оказался белым. Найти вероятность того, что этот шар был вынут из урны третьего состава.
— по 3 белых и 2 черных шара. Из одной наудачу выбранной урны взят шар, он оказался белым. Найти вероятность того, что этот шар был вынут из урны третьего состава.
6. Известно, что 96 % выпускаемой продукции удовлетворяют стандарту. Упрощенная схема контроля признает пригодной стандартную продукцию с вероятностью 0,98 и нестандартную — с вероятностью 0,05. Определить вероятность того, что изделие, прошедшее упрощенный контроль, удовлетворяет стандарту.
7.Два баскетболиста делают по три броска мячом в корзину. Вероятности попадания мяча при каждом броске равны соответственно 0,6 и 0,7. Найти вероятность того, что у первого баскетболиста будет больше попаданий, чем у второго.
8. Имеется 10 одинаковых по виду урн, из которых в 9 находится по два черных и два белых шара, а в одной — пять белых и один черный шар. Из урны, взятой наудачу, извлечен белый шар. Какова вероятность того, что он извлечен из урны, содержащей пять белых шаров?
9. В каждом из трех матчей футбольного турнира команда с вероятностью 0,2 одерживает победу, получая за нее 2 очка, с вероятностью 0,5 играет вничью, получая 1 очко, и с вероятностью 0,3 терпит поражение, не получая за это очков. Найти закон распределения и дисперсию общего числа набранных очков.
10. Попадание случайной точки в любое место области 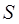 равновозможно, а область
равновозможно, а область 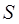 состоит из четырех частей, составляющих соответственно 50, 30, 12 и 8 % всей области. При испытании имело место событие
состоит из четырех частей, составляющих соответственно 50, 30, 12 и 8 % всей области. При испытании имело место событие 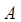 , которое происходит только при попадании точки в одну из этих частей с вероятностями соответственно 0,01, 0,05, 0,2 и 0,5. В какую из частей области
, которое происходит только при попадании точки в одну из этих частей с вероятностями соответственно 0,01, 0,05, 0,2 и 0,5. В какую из частей области 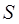 вероятнее всего произошло попадание?
вероятнее всего произошло попадание?
Date: 2015-06-06; view: 745; Нарушение авторских прав