
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Формула Тейлора для функции двух переменных
Формула Тейлора для функции одной переменной 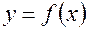 выглядит следующим образом:
выглядит следующим образом:
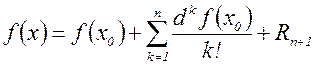 .
.
Здесь 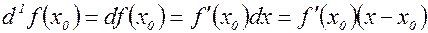 – дифференциал первого порядка;
– дифференциал первого порядка;
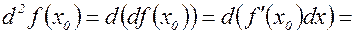
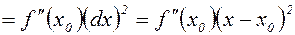 – дифференциал второго порядка;
– дифференциал второго порядка;
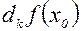 – дифференциал
– дифференциал 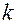 -го порядка;
-го порядка;
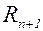 – остаточный член.
– остаточный член.
Формула Тейлора позволяет вычислить функцию  в окрестности точки
в окрестности точки 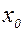 , если в этой точке известны функция и ее
, если в этой точке известны функция и ее 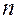 производных.
производных.
Аналогичная формула имеет место для функции двух переменных и вообще для функции многих переменных. В частности, если 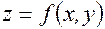 – функция двух переменных, непрерывная вместе со своими
– функция двух переменных, непрерывная вместе со своими 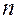 частными производными по
частными производными по 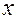 и
и 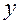 в некоторой области, содержащей точки
в некоторой области, содержащей точки 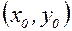 и
и 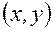 , то имеет место следующая формула Тейлора:
, то имеет место следующая формула Тейлора:
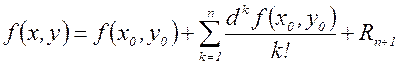 .
.
Здесь 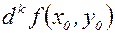 – полный дифференциал
– полный дифференциал 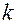 -го порядка функции двух переменных.
-го порядка функции двух переменных.
Выпишем эти дифференциалы при 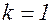 и
и 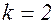 .
.
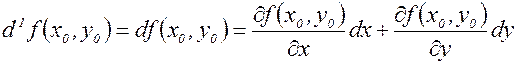 ,
,
где 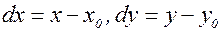 . Таким образом,
. Таким образом, 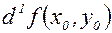 – обычный полный дифференциал первого порядка. При
– обычный полный дифференциал первого порядка. При 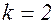 имеем
имеем
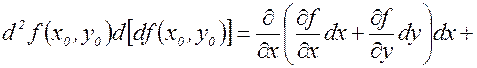
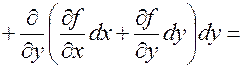
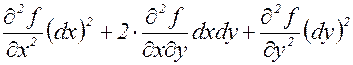 .
.
Упражнение. Выписать самостоятельно полный дифференциал третьего порядка функции двух переменных.
Замечание. Если  , то формула Тейлора носит название формулы Маклорена.
, то формула Тейлора носит название формулы Маклорена.
Пример 1.
Разложить функцию 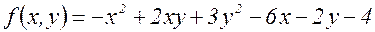 по формуле Тейлора в окрестности точки
по формуле Тейлора в окрестности точки 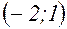 .
.
Сначала найдем частные производные:
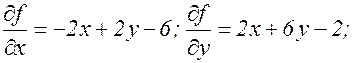
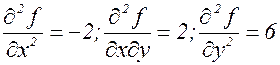 .
.
Все остальные производные равны нулю, так что формула Тейлора имеет ограниченное число членов.
Найдем функцию и ее частные производные в точке 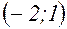 .
.
 ;
;
вторые частные производные равны константам, которые мы уже вычислили. Таким образом,

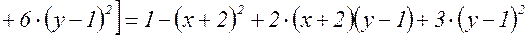 .
.
Пример 2.
Используя формулу Тейлора до членов второго порядка включительно, вычислить приближенно значение 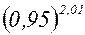 .
.
Пусть  .
.
Тогда

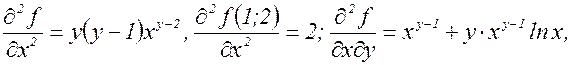
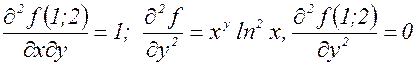 .
.
Таким образом,


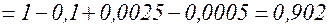 .
.
3.13. Экстремум функции двух переменных
Определение 1. Функция z=f(x,y) имеет максимум в точке M0(x0,y0), если f(x0,y0)>f(x,y) для всех точек (х,у), достаточно близких к точке (х0,у0) и отличных от нее.
Определение 2. Функция z=f(x,y) имеет минимум в точке M0(x0,y0), если f(x0,y0)<f(x,y) для всех точек (х,у), достаточно близких к точке (х0,у0) и отличных от нее.
Как обычно, точки максимума и минимума называют точками экстремума.
Пример. Рассмотрим функцию z=(x–a)2+(y–b)2+1.
Очевидно, при х=а и у=b, z=1. Но если х¹а, у¹b, то
(x–a)2+(y–b)2>0, поэтому в любой точке, отличной от М(а,b), z>1. Следовательно, в точке М(а,b) функция имеет минимум, т.к. z(a,b)<z(x,y).
Можно дать немного другие определения. Пусть
Df = f(x, y) – f(x0, y0) = f(x0 + Dx, y0 + Dy) – f(x0, y0).
Определение. Если Df>0 (Df<0) при всех достаточно малых приращениях независимых переменных, то функция f(x,y) достигает в точке М(х0,у0) минимума (максимума).
Все приведенные формулировки переносятся на функции любого числа переменных.
Теорема 1 (необходимое условие экстремума).
Если функция z=f(x,y) достигает экстремума при х=х0, у=у0, то каждая частная производная первого порядка от z или обращается в ноль, или не существует при х=х0, у=у0.
Доказательство очевидно, привести его самостоятельно.
Замечание. Условия 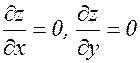 являются необходимыми, но не достаточными. Может оказаться, что оба эти условия выполнены, а экстремума нет.
являются необходимыми, но не достаточными. Может оказаться, что оба эти условия выполнены, а экстремума нет.
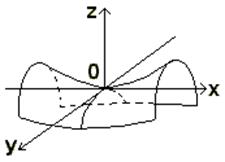
Пример. z=x2–y2.
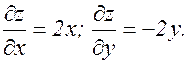
В точке х0=0, у0=0 обе частные производные равны нулю, но ни максимума, ни минимума нет (см. рис.).
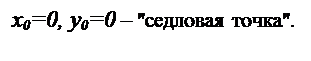
Теорема 2 (достаточное условие экстремума).
Пусть в некоторой области, содержащей точку М0(х0,у0) функция f(x,y) имеет непрерывные частные производные до третьего порядка включительно; пусть, кроме того, точка М0(х0,у0) является критической точкой, т.е.
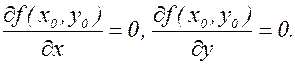
Тогда при х=х0, у=у0:
1) f(x,y) имеет максимум, если
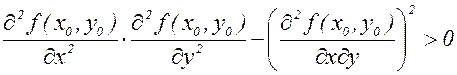
и 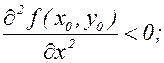
2) f(x,y) имеет минимум, если
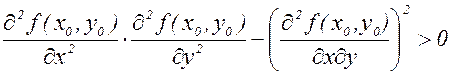
и 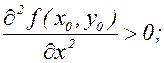
3) f(x,y) не имеет ни максимума, ни минимума, если
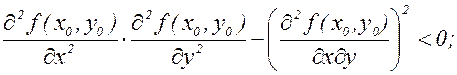
4) если же 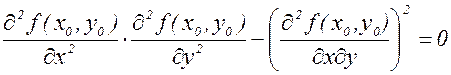 , то экстремум может быть, а может его и не быть (требуется дополнительное исследование).
, то экстремум может быть, а может его и не быть (требуется дополнительное исследование).
Теорема 2 дается без доказательства.
Пример. Исследовать на максимум и минимум функцию z=x3+y3–3xy.
Сначала находим критические точки:
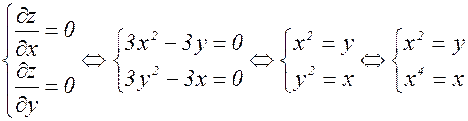 .
.
Решим уравнение x4=x:
x4–x=0, x(x3–1)=0, x(x–1)(x2+x+1)=0, x1=0, x2=1.
Тогда у1=0, у2=1. Таким образом, мы нашли две критические точки: (0;0) и (1;1).
Найдем производные второго порядка:
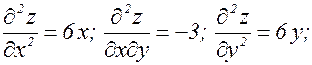
Исследуем характер точки (0;0):

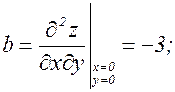
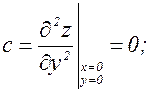
ac – b2 = 0 × 0 – 9 = –9 < 0.
В этой точке экстремума нет.
Исследуем характер второй точки (1;1):
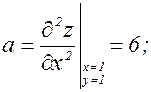 b=–3;
b=–3; 
ac – b2 = 6 × 6 – 9 = 27 > 0; a > 0.
В точке (1;1) функция имеет минимум, zmin=z(1;1)=–1.
3.14. Условный экстремум функции многих переменных
Под условным экстремумом функции понимают экстремум функции не для независимых аргументов, а для аргументов, связанных некоторым условием (например, уравнением).
Рассмотрим такую задачу: имеется кусок жести площадью 2a. Надо сделать из него закрытую коробку в форме прямоугольного параллелепипеда, имеющую наибольший объем.
Пусть х, у, z – ребра параллелепипеда, тогда его объем равен V = xyz. (3.14.1)
Надо найти максимум этой функции при условии, что
2ху+2xz+2yz=2a. (3.14.2)
Это и есть задача на условный экстремум: переменные связаны условием (3.14.2).
В общем случае (при наличии одного условия) задача ставится так: требуется найти экстремум функции
u=f(x,y) (3.14.3)
при условии, что х и у связаны уравнением
j(х,у)=0. (3.14.4)
При наличии условия (3.14.4) из двух переменных х и у независимой будет только одна, например, х, т.к. у определяется из (3.14.4) как функция от х. Если уравнение (3.14.4) можно разрешить относительно у, то, подставив это выражение в (3.14.3), получим функцию одной переменной х и сведем задачу к нахождению обычного, т.е. безусловного экстремума. Нас будет интересовать общий случай, когда уравнение (3.14.4) невозможно разрешить относительно одной из переменных.
Поскольку функция u должна иметь экстремум, то  , т.е.
, т.е.
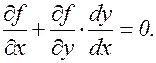 (3.14.5)
(3.14.5)
Дифференцируя равенство (3.14.4) по х, найдем
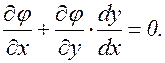 (3.14.6)
(3.14.6)
Для решения уравнений (3.14.5) и (3.14.6) применим прием, носящий имя Лагранжа. Умножим (3.14.6) на неопределенный пока множитель l (множитель Лагранжа), сложим с (3.14.5) и получим
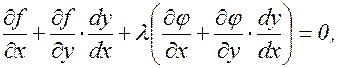 или
или
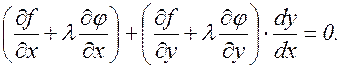 (3.14.7)
(3.14.7)
Функцию F(x,y,l)=f(x,y)+lj(x,y) в теории условного экстремума называют функцией Лагранжа.
Подберем l так, чтобы

Тогда из (3.14.7):
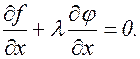
Таким образом, дело свелось к решению системы
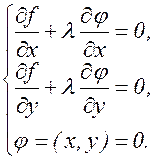 (3.14.8)
(3.14.8)
В этой системе три неизвестных: l, х и у. Параметр Лагранжа l играет вспомогательную роль. Формально систему (3.14.8) можно получить так: приравнять нулю все частные производные от функции Лагранжа (по х, у и l).
(3.14.8) – это необходимое условие экстремума. Характер же экстремума и ответ на вопрос: "есть ли экстремум" определяется после нахождения критических точек с помощью достаточного критерия экстремума.
Рассмотрим задачу изготовления коробки максимального объема.
Нам надо найти максимум функции
V=xyz
при условии, что
ху+xz+yz–a=0 (x>0, y>0, z>0).
Составим функцию Лагранжа:
F(x,y,z,l)=xyz+l(xy+xz+yz–a).
Найдем ее частные производные по x, y, z, l и приравняем их нулю:
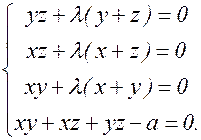
Эту систему удобно решать так: умножим первое уравнение на х, второе – на у, третье – на z и сложим их.
3xyz+l(2xy+2xz+2yz)=0.
С учетом четвертого уравнения 3xyz+l×2a=0, т.е.
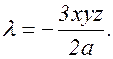
Подставим выражение для l в первые три уравнения:
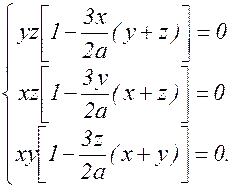
Т.к. x>0, y>0, z>0, то нулями могут быть только выражения в квадратных скобках, т.е.

Из первых двух уравнений ясно, что х=у, а из второго и третьего, что у=z. Таким образом,  . Это единственная система значений, при которых возможен максимум или минимум.
. Это единственная система значений, при которых возможен максимум или минимум.
Из геометрических соображений ясно, что это максимум, т.к. объем коробки не может быть неограниченно большим. Можно это утверждение доказать строго, но обычно вполне достаточно геометрических соображений.
Итак, чтобы коробка имела максимальный объем, необходимо, чтобы она имела форму куба с ребром 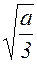 .
.
Date: 2015-09-02; view: 1432; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |