Наибольшее и наименьшее значения функции на отрезке

Наибольшим значением функции на отрезке называется самое большое из всех ее значений на этом отрезке, а наименьшим – самое маленькое из всех ее значений.

Рассмотрим функцию y=f(x) непрерывную на отрезке [ a, b ]. Как известно, такая функция достигает своего наибольшего и наименьшего значений, либо на границе отрезка, либо внутри него. Если наибольшее или наименьшее значение функции достигается во внутренней точке отрезка, то это значение является максимумом или минимумом функции, то есть достигается в критических точках.

Таким образом, получаем следующее правило нахождения наибольшего и наименьшего значений функции на отрезке[ a, b ]:

1. Найти все критические точки функции в интервале (a, b) и вычислить значения функции в этих точках.

2. Вычислить значения функции на концах отрезка при x = a, x = b.

3. Из всех полученных значений выбрать наибольшее и наименьшее.

Примеры.

1. Найти наибольшее и наименьшее значения функции 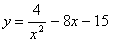на отрезке [–2; –0,5].

Найдем критические точки функции.

Вычислим значения функции в найденной точке и на концах заданного отрезка.

Итак,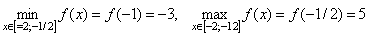

2. Найти наибольшее и наименьшее значения функции y=x -2·ln x на [1; e].

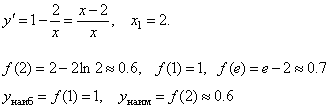
3. Чему равна наименьшая площадь боковой поверхности прямого кругового конуса объема 3π?

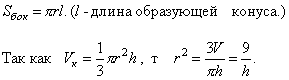
По теореме Пифагора

.

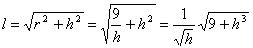Следовательно, .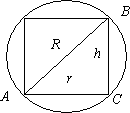

.

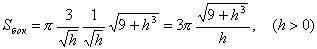Найдем критические точки функции S: S ' = 0, т.е.

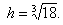
Покажем, что при найденном значении h функция S_бок достигает минимума.

.

4.

Найти радиус основания и высоту цилиндра наибольшего объема, который можно вписать в шар радиусом R.

Пусть r – радиус основания цилиндра, h – высота.

Нам нужно максимизировать объем цилиндра .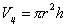

Используя условие задачи, найдем связь между r и h. По теореме Пифагора из треугольника ABC следует, что 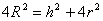. Отсюда .

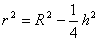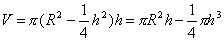, по смыслу задачи 0≤ h ≤2 R.

.

Покажем, что при найденном значении h функция V принимает наибольшее значение.

1.

a. Найти ОДЗ и точки разрыва функции.

b. Найти точки пересечения графика функции с осями координат.

2. Провести исследование функции с помощью первой производной, то есть найти точки экстремума функции и интервалы возрастания и убывания.

3. Исследовать функцию с помощью производной второго порядка, то есть найти точки перегиба графика функции и интервалы его выпуклости и вогнутости.

4. Найти асимптоты графика функции: а) вертикальные, b) наклонные.

5. На основании проведенного исследования построить график функции.

Заметим, что перед построением графика полезно установить, не является ли данная функция четной или нечетной.

Вспомним, что функция называется четной, если при изменении знака аргумента значение функции не меняется: f(-x) = f(x) и функция называется нечетной, если f(-x) = -f(x).

В этом случае достаточно исследовать функцию и построить её график при положительных значениях аргумента, принадлежащих ОДЗ. При отрицательных значениях аргумента график достраивается на том основании, что для четной функции он симметричен относительно оси Oy, а для нечетной относительно начала координат.

Примеры. Исследовать функции и построить их графики.

1. .

1. Область определения функции D(у)= (–∞; +∞). Точек разрыва нет.

Пересечение с осью Ox: x = 0, у= 0.

Функция нечетная, следовательно, можно исследовать ее только на промежутке [0, +∞).

2. 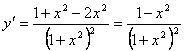. Критические точки: x₁ = 1; x₂ = –1.

3.

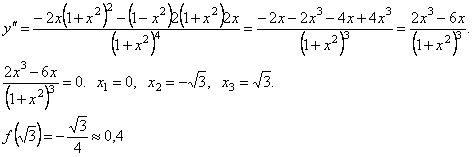
4. а) Вертикальных асимптот нет

б) . Асимптота – y = 0.

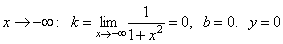
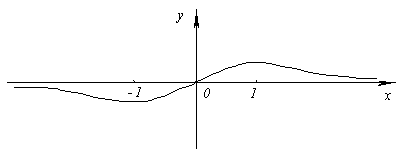
2. .

1. D(y)= (–∞; +∞). Точек разрыва нет.

Пересечение с осью Ox: .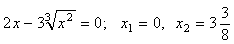

2.

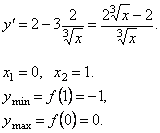
3. .

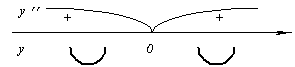
4. а) Вертикальных асимптот нет

б) .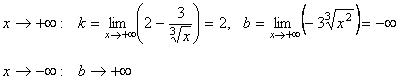

Наклонных асимптот нет.

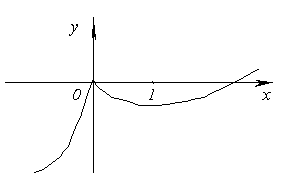
3. .

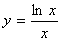1. D(y)= (0; +∞). Функция непрерывна на области определения.

Пересечение с осью :

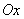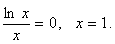
2.

3.

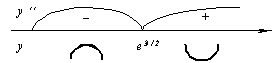
4. а) .

Вертикальная асимптота x = 0.

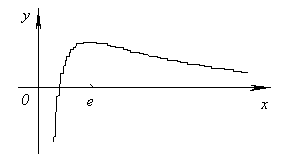
б) .

Наклонная асимптота y = 0.

4. .

1. D(y)= (–∞;0)(0;1)(1;+∞).

Функция имеет две точки разрыва x = 0 и x = 1.

Точек пересечения с осями координат нет.

2. 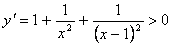при любых действительных значениях x. Поэтому функция возрастает на всей числовой прямой.

3.

4.

а)

Вертикальные асимптоты x = 0, x = 1.

б)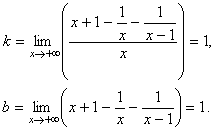

Наклонная асимптота y = x + 1.