
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Необходимые и достаточные условия возрастания и убывания функции
Вспомним сначала определения возрастающей и убывающей функций.
Функция y=f(x), определенная на некотором отрезке [ a, b ] (интервале (a, b)), называется возрастающей на этом отрезке, если большему значению аргумента x из [ a, b ]  соответствует большее значение функции, то есть если x 1 < x 2, то f(x 1 ) < f(x 2 ).
соответствует большее значение функции, то есть если x 1 < x 2, то f(x 1 ) < f(x 2 ).
Функция y=f(x) называется убывающей на некотором отрезке [ a, b ], если меньшему значению аргумента x из [ a, b ]соответствует большее значение функции, то есть если x 1 < x 2, то f(x 1 ) > f(x 2 ).
Функция, только возрастающая или только убывающая на отрезке, называется монотонной на этом отрезке.
Функция y=f(x) называется постоянной на некотором отрезке [ a, b ], если при изменении аргумента x она принимает одни и те же значения.
Рассмотрим график функции изображенной на рисунке и определим промежутки возрастания и убывания функции.
(-∞, a), (c, +∞) – убывает;
(a, b) – постоянная;
(b, c) – возрастает.
Применим понятие производной для исследования возрастания и убывания функции.
Теорема 1. (Необходимое и достаточное условия возрастания функции)
1. Если дифференцируемая функция y=f(x) возрастает на [ a, b ], то ее производная неотрицательна на этом отрезке, f '(x) ≥ 0.
2. Обратно. Если функция y=f(x) непрерывна на [ a, b ], дифференцируема на (a, b) и ее производная положительна на этом отрезке, f ' (x) ≥ 0 для a<x<b, то f(x) возрастает на[ a, b ].
Доказательство.
1. Докажем первую часть теоремы. Итак, пусть функция y=f(x) возрастает на [ a, b ]. Зафиксируем на этом отрезке произвольную точку x, придадим ей приращение Δ x. Тогда если Δ x >0, то x<x+ Δ x. Поэтому по определению возрастающей функции f(x)<f(x+ Δ x), то есть f(x+ Δ x) - f(x)> 0. Но тогда и 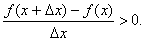 Аналогично, если Δ x< 0, то x>x+ Δ x и значит f(x+ Δ x)-f(x)< 0, а
Аналогично, если Δ x< 0, то x>x+ Δ x и значит f(x+ Δ x)-f(x)< 0, а 
Переходя в этом равенстве к пределу при Δ x →0, получим  , то есть f '(x) ≥0.
, то есть f '(x) ≥0.
2. Докажем вторую часть теоремы. Пусть f '(x)> 0при всех x (a,b). Рассмотрим два любых значения x 1 и x 2 таких, что x 1 < x 2. Нужно доказать, что f(x 1 )< f(x 2 ). По теореме Лагранжа существует такое число c (x 1, x 2 ), что 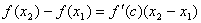 . По условию f '(x)> 0, x 1 – x 2>0
. По условию f '(x)> 0, x 1 – x 2>0 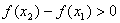 , а это и значит, что f(x) – возрастающая функция.
, а это и значит, что f(x) – возрастающая функция.
Аналогичная теорема имеет место и для убывающих функций.
Теорема 2. Если f(x) убывает на[ a,b ], то  на этом отрезке. Если на этом отрезке. Если 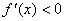 на (a; b), то f(x) убывает на [ a, b ],в предположении, что f(x) непрерывна на [ a, b ].
Доказанная теорема выражает очевидный геометрический факт. Если на [ a, b ] функция возрастает, то касательная к кривой y=f(x) в каждой точке этого отрезке образует острый угол с осью Ox или горизонтальна, т.е. tg a≥0, а значит f '(x) ≥0.
Аналогично иллюстрируется и вторая часть теоремы.
Таким образом, возрастание и убывание функции характеризуется знаком ее производной. Чтобы найти на каком промежутке функция возрастает или убывает, нужно определить, где производная этой функции только положительна или только отрицательна, то есть решить неравенства f '(x) >0 – для возрастания или f '(x)< 0 – для убывания.
Примеры. Определить интервалы монотонности функции.
3. на (a; b), то f(x) убывает на [ a, b ],в предположении, что f(x) непрерывна на [ a, b ].
Доказанная теорема выражает очевидный геометрический факт. Если на [ a, b ] функция возрастает, то касательная к кривой y=f(x) в каждой точке этого отрезке образует острый угол с осью Ox или горизонтальна, т.е. tg a≥0, а значит f '(x) ≥0.
Аналогично иллюстрируется и вторая часть теоремы.
Таким образом, возрастание и убывание функции характеризуется знаком ее производной. Чтобы найти на каком промежутке функция возрастает или убывает, нужно определить, где производная этой функции только положительна или только отрицательна, то есть решить неравенства f '(x) >0 – для возрастания или f '(x)< 0 – для убывания.
Примеры. Определить интервалы монотонности функции.
3.  . Область определения заданной функции D(y) = (-∞; 0)(0; +∞). . Область определения заданной функции D(y) = (-∞; 0)(0; +∞).
 . Следовательно, f(x) – убывает на (-∞; 0) и (0; +∞).
4. . Следовательно, f(x) – убывает на (-∞; 0) и (0; +∞).
4.
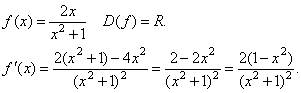 Найдем промежутки, на которых производная заданной функции положительна или отрицательна методом интервалов.
Итак, f(x) – убывает на (–∞; –1] и [1; +∞), возрастает на отрезке [–1; 1].
5.
Найдем промежутки, на которых производная заданной функции положительна или отрицательна методом интервалов.
Итак, f(x) – убывает на (–∞; –1] и [1; +∞), возрастает на отрезке [–1; 1].
5.
 .
Используя метод интервалов, получим f(x) убывает на (0; 1) и (1; e], возрастает на [e; +∞). .
Используя метод интервалов, получим f(x) убывает на (0; 1) и (1; e], возрастает на [e; +∞).
|   
|
Рассмотрим график непрерывной функции y=f(x), изображенной на рисунке. Значение функции в точке x 1 будет больше значений функции во всех соседних точках как слева, так и справа от x 1. В этом случае говорят, что функция имеет в точке x 1 максимум. В точке x 3 функция, очевидно, также имеет максимум. Если рассмотреть точку x 2, то в ней значение функции меньше всех соседних значений. В этом случае говорят, что функция имеет в точке x 2 минимум. Аналогично для точки x 4.
Функция y=f(x) в точке x 0 имеет максимум, если значение функции в этой точке больше, чем ее значения во всех точках некоторого интервала, содержащего точку x 0, т.е. если существует такая окрестность точки x 0, что для всех x ≠ x 0, принадлежащих этой окрестности, имеет место неравенство f(x) < f(x 0 ).
Функция y=f(x) имеет минимум в точке x 0, если существует такая окрестность точки x 0, что для всех x ≠ x 0, принадлежащих этой окрестности, имеет место неравенство f(x) > f(x0.
Точки, в которых функция достигает максимума и минимума, называются точками экстремума, а значения функции в этих точках экстремумами функции.
Обратим внимание на то, что функция, определенная на отрезке, может достигать максимума и минимума только в точках, заключенных внутри рассматриваемого отрезка.
Отмети, что если функция имеет в точке максимум, то это не означает, что в этой точке функция имеет наибольшее значение во всей области определения. На рисунке, рассмотренном выше, функция в точке x 1 имеет максимум, хотя есть точки, в которых значения функции больше, чем в точке x 1. В частности, f (x 1) < f (x 4) т.е. минимум функции больше максимума. Из определения максимума следует только, что это самое большое значение функции в точках, достаточно близкихк точке максимума.
Теорема 1. (Необходимое условие существования экстремума.) Если дифференцируемая функция y=f(x) имеет в точке x= x 0 экстремум, то ее производная в этой точке обращается в нуль.
Доказательство. Пусть для определенности в точке x 0 функция имеет максимум. Тогда при достаточно малых приращениях Δ x имеем f(x 0+ Δ x)<f(x 0 ), т.е. 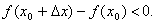 Но тогда
Но тогда
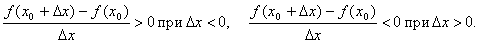
Переходя в этих неравенствах к пределу при Δ x → 0 и учитывая, что производная f '(x 0) существует, а следовательно предел, стоящий слева, не зависит от того как Δ x → 0, получаем: при Δ x → 0 – 0 f' (x 0) ≥ 0 а при Δ x → 0 + 0 f' (x 0) ≤ 0. Так как f ' (x 0) определяет число, то эти два неравенства совместны только в том случае, когда f ' (x 0) = 0.
Доказанная теорема утверждает, что точки максимума и минимума могут находиться только среди тех значений аргумента, при которых производная обращается в нуль.
Мы рассмотрели случай, когда функция во всех точках некоторого отрезка имеет производную. Как же обстоит дело в тех случаях, когда производная не существует? Рассмотрим примеры.
Примеры.
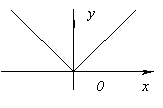
1. y =| x |.
Функция не имеет производной в точке x =0 (в этой точке график функции не имеет определенной касательной), но в этой точке функция имеет минимум, так как y (0)=0, а при всех x ≠ 0 y > 0.
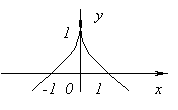
2.
Функция  не имеет производной при x =0, так как не имеет производной при x =0, так как  обращается в бесконечность при x =0. Но в этой точке функция имеет максимум.
3.
Функция обращается в бесконечность при x =0. Но в этой точке функция имеет максимум.
3.
Функция  не имеет производной при x =0, так как не имеет производной при x =0, так как 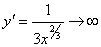 при x →0. В этой точке функция не имеет ни максимума, ни минимума. Действительно, f(x) =0 и при x <0 f(x) <0, а при x >0 f(x) >0.
Таким образом, из приведенных примеров и сформулированной теоремы видно, что функция может иметь экстремум лишь в двух случаях: 1) в точках, где производная существует и равна нулю; 2) в точке, где производная не существует.
Однако, если в некоторой точке x 0 мы знаем, что f '(x 0 ) =0, то отсюда нельзя делать вывод, что в точке x 0 функция имеет экстремум.
Например. при x →0. В этой точке функция не имеет ни максимума, ни минимума. Действительно, f(x) =0 и при x <0 f(x) <0, а при x >0 f(x) >0.
Таким образом, из приведенных примеров и сформулированной теоремы видно, что функция может иметь экстремум лишь в двух случаях: 1) в точках, где производная существует и равна нулю; 2) в точке, где производная не существует.
Однако, если в некоторой точке x 0 мы знаем, что f '(x 0 ) =0, то отсюда нельзя делать вывод, что в точке x 0 функция имеет экстремум.
Например.  .
Но точка x =0 не является точкой экстремума, поскольку слева от этой точки значения функции расположены ниже оси Ox, а справа выше.
Значения аргумента из области определения функции, при которых производная функции обращается в нуль или не существует, называются критическими точками. .
Но точка x =0 не является точкой экстремума, поскольку слева от этой точки значения функции расположены ниже оси Ox, а справа выше.
Значения аргумента из области определения функции, при которых производная функции обращается в нуль или не существует, называются критическими точками.
|    
|
Из всего вышесказанного следует, что точки экстремума функции находятся среди критических точек, и, однако, не всякая критическая точка является точкой экстремума. Поэтому, чтобы найти экстремум функции, нужно найти все критические точки функции, а затем каждую из этих точек исследовать отдельно на максимум и минимум. Для этого служит следующая теорема.
Теорема 2. (Достаточное условие существования экстремума.) Пусть функция непрерывна на некотором интервале, содержащем критическую точку x 0, и дифференцируема во всех точках этого интервала (кроме, быть может, самой точки x 0). Если при переходе слева направо через эту точку производная меняет знак с плюса на минус, то в точке x = x 0 функция имеет максимум. Если же при переходе через x 0 слева направо производная меняет знак с минуса на плюс, то функция имеет в этой точке минимум.
Таким образом, если
a. f '(x) >0 при x < x 0 и f '(x)< 0 при x> x 0, то x 0 – точка максимума;
b.  при x < x 0 и f '(x)> 0 при x> x 0, то x 0 – точка минимума.
при x < x 0 и f '(x)> 0 при x> x 0, то x 0 – точка минимума.
Доказательство. Предположим сначала, что при переходе через x 0 производная меняет знак с плюса на минус, т.е. при всех x, близких к точке x 0 f '(x)> 0 для x< x 0, f '(x)< 0 для x> x 0. Применим теорему Лагранжа к разности f(x) - f(x 0 ) = f '(c)(x- x 0), где c лежит между x и x 0.
1. Пусть x < x 0. Тогда c< x 0 и f '(c)> 0. Поэтому f 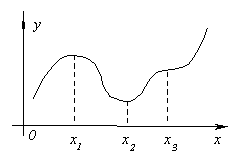 '(c)(x- x 0) < 0и, следовательно,
'(c)(x- x 0) < 0и, следовательно,
f(x) - f(x 0 )< 0,т.е. f(x)< f(x 0 ).
2. Пусть x > x 0. Тогда c> x 0 и f '(c)< 0. Значит f '(c)(x- x 0) < 0. Поэтому f(x) - f(x 0 ) <0,т.е. f(x) < f(x 0 ).
Таким образом, для всех значений x достаточно близких к x 0 f(x) < f(x 0 ). А это значит, что в точке x 0 функция имеет максимум.
Аналогично доказывается вторая часть теоремы о минимуме.
Проиллюстрируем смысл этой теоремы на рисунке. Пусть f '(x 1 ) =0 и для любых x, достаточно близких к x 1, выполняются неравенства
f '(x)< 0 при x< x 1, f '(x)> 0 при x> x 1.
Тогда слева от точки x 1 функция возрастает, а справа убывает, следовательно, при x = x 1 функция переходит от возрастания к убыванию, то есть имеет максимум.
Аналогично можно рассматривать точки x 2 и x 3.

Схематически все вышесказанное можно изобразить на картинке:
Правило исследования функции y=f(x) на экстремум
1. Найти область определения функции f(x).
2. Найти первую производную функции f '(x).
3. Определить критические точки, для этого:
a. найти действительные корни уравнения f '(x) =0;
b. найти все значения x при которых производная f '(x) не существует.
4. Определить знак производной слева и справа от критической точки. Так как знак производной остается постоянным между двумя критическими точками, то достаточно определить знак производной в какой-либо одной точке слева и в одной точке справа от критической точки.
5. Вычислить значение функции в точках экстремума.
Примеры. Исследовать функции на минимум и максимум.
1. 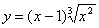 . Область определения функции D(y)=R.
. Область определения функции D(y)=R.
Найдем производную заданной функции 
Определим критические точки  . Производная не существует при х 2= 0. Следовательно, критические точки: 0 и 2/5. Нанесем их на числовую ось и определим знак производной на каждом из полученных промежутков.
. Производная не существует при х 2= 0. Следовательно, критические точки: 0 и 2/5. Нанесем их на числовую ось и определим знак производной на каждом из полученных промежутков.

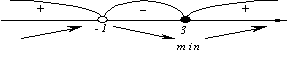


2.
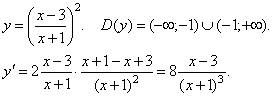
Критическая точка функции x =3. Точка x = –1 не входит в область определения функции.
3. 

Date: 2015-09-02; view: 16548; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |