Определение 3

Кафедра математики

ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ

Методические указания к самостоятельному изучению соответствующего раздела курса математики для студентов всех специальностей

Составители:

В.П.Кузнецов

Л.Е.Мякишева

Ю.А.Фадеев

Утверждены на заседании кафедры

Протокол № 4 от 14.января.2011г.

Рекомендованы к печати

Учебно-методической комиссией

специальности 150402

Протокол № 4 от 18.01.2011г.

Электронная копия

Хранится в библиотеке

Главного корпуса ГУ КузГТУ

Кемерово 2011

ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ

Введение: анализ функций нескольких переменных…………….…..3

Основные понятия………………………………………………………….3

2. Скалярное поле…………………………………………………………......6

Предел функции нескольких переменных…………………………..…9

Непрерывность функции нескольких переменных…………………10

Дифференцирование функций нескольких переменных…………….12

Частные производные……………………………………………………12

Условия дифференцируемости………………………………………….15

Производная по направлению………………………………………….18

Градиент……………………………………………………………………..21

Сложные функции нескольких переменных…………………………..22

1. Понятия сложной функции………………………………………………22

Неявные функции…………………………………………………………...29

Определение неявной функции и еёусловие существования…...29

Дифференцирование неявной функции……………………………….30

Производные и дифференциалы высших порядков…………………31

Частные производные высших порядков…………………………….31

Дифференциалы высших порядков…………………………………….32

Формула тейлора…………………………………………………………..34

Экстремумы функций нескольких переменных……………………….35

Точки максимума и минимума…………………………………………..35

Необходимые условия экстремума……………………………………35

Достаточные условия экстремума…………………………………….35

Условный экстремум……………………………………………………...37

Наибольшее и наименьшее значение………………………………….40

Список литературы..........................................................................43

Введение: анализ функций нескольких переменных

Основные понятия

Определение 1. Функцией 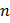переменных 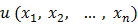называется отображение 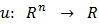, т.е. любое правило, которое каждой точке ставит в соответствие действительное число .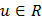

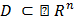называется областью определения функции 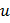и записывается .

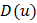Функцию 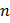переменных записывают так: .

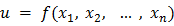Пространство 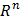считаем евклидовым с ортонормированным базисом.

Определение 2. Множество точек 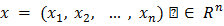, удовлетворяющих неравенству

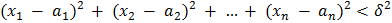
называется открытым n– мерным шаром радиуса 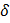с центром в точке 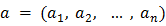, или 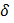– окрестностью точки .

Символом 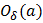обозначается проколотая окрестность точки 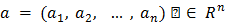, т.е. множество точек , удовлетворяющих неравенствам

.

Определение 3.

1. Точка 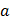называется внутренней точкой множества 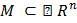, если существует окрестность точки , все точки которой принадлежат данному множеству .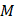

2. Точка 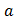называется граничной точкой множества 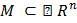, если любая окрестность точки содержит как точки, принадлежащие данному множеству 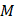, так и не принадлежащие этому множеству.

3. Множество всех граничных точек множества называется его границей.

4. Точка называется предельной точкой множества, если любая окрестность точки 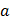содержит точки принадлежащие данному множеству, отличные от .

Date: 2015-07-27; view: 298; Нарушение авторских прав