Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Метод производящий функций
Этот метод используется для перечисления комбинаторных чисел и установления комбинаторных тождеств.
Исходным пунктом являются последовательность {ai} комбинаторных чисел и последовательность функций {φi(x)} (i = 0, 1, …).
Рассмотрим ряд
,
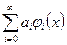который, в случае, когда последовательность {ai} конечна, т.е. 0 ≤ i ≤ n, будет многочленом.
При определенных ограничениях данный ряд будет сходящимся и тогда он в некоторой области будет задавать функцию F(x):
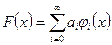
Эта функция называется производящей функцией.
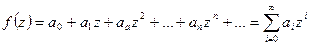или
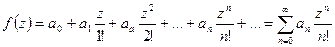- экспоненциальная производящая функция.
Пример 1.
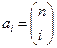(i=0,1, …, n), φi(x)-xi
В этом случае имеем
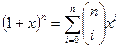
В качестве производящей функции здесь будет бином Ньютона.
С помощью производящей функции установим тождество
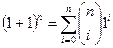
Для этого возьмем тождество
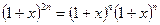
Оно эквивалентно тождеству
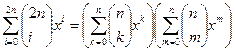
Сравнивая коэффициенты при xn, получим
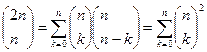
Пример 1.
Применение метода производящей функции, когда функция определяется степенным рядом.
Последовательность чисел fn называется числами Фибоначчи, задается рекуррентными соотношениями fn = fn-1+ fn-2 и f0 = f1 = 1
Возьмем φn(x) = xn (n = 0,1, 2, …). С этой последовательностью связан ряд
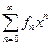
который в силу fn ≤ 2n (поскольку fn ≤ 2fn-1) сходится при │ x│ < ½ и определяет производящую функцию F(x)
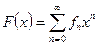
Так как
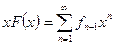
и
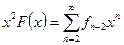
то
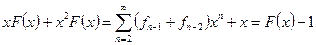
или
(1-x-x2)F(x) =1
Отсюда находим явный вид производящей функции F(x):
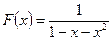
Решая уравнение x2 + x – 1 = 0 находим его корни
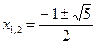
Найдем разложение F(x) на элементарные дроби
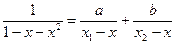
Имеем ax2 + bx1 – (a + b)x = -1
Это справедливо, если a = - b и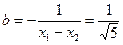 
.
Далее, воспользовавшись формулой для суммы убывающей геометрической прогрессии (при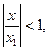 
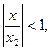) получим
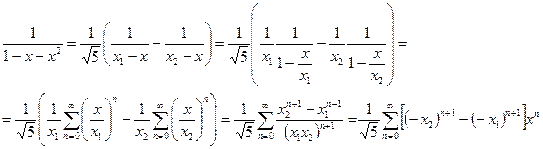
откуда
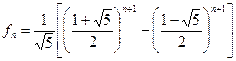
что дает явное выражение для чисел Фибоначчи.
Контрольные вопросы
1. Что такое комбинаторика и для чего она нужна?
2. Что называется:
— перестановкой п -элементного множества;
— размещением из п элементов по т элементов;
— сочетанием из п элементов по т элементов?
3. В чем отличие размещений от перестановок?
4. В чем отличие сочетаний от размещений?
5. Сколькими способами можно разместить три книги на книжной полке?
6. Запишите формулу для вычисления числа сочетаний элементов, используемую в формуле бинома Ньютона.
7. Как найти число перестановок с повторениями?
8. Сколько существует пятизначных чисел, у которых каждая следующая цифра:
—меньше предыдущей,
— больше предыдущей.
9. Сколько прямых можно провести через п точек, если никакие три из них не лежат на одной прямой?
10. Сколько разных слов можно составить перестановкой букв в слове «чачача»?
11. Вычислите: (а + b + с)2; (а + b + с)3.
12. Покажите, что сумма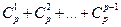 
делится на р, где р — простое число.
13. Докажите свойства биномиальных коэффициентов.
Date: 2015-07-24; view: 457; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |