Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Комбинаторные числа Стирлинга и Белла
Пусть card(M) = n и k — число непустых подмножеств, на которые разбивается множество M. Рассмотрим разбиение множества M = {а1, а2, аn}. Обозначим через S(n,k) - число разбиений множества на k (n>0, 0<k≤n) непустых частей, а через B(n) – число всех разбиений множества M(n>0) на непустые части.
Тогда S(n,k) будем называть число способов разбить множество M мощностью n на k непустых множества.
S(0,0) = 1
S(n,0) = 0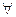 
n≠1
Числа S(n,k) называются числами Стирлинга.
Числа Стирлинга:
| nk | |||||||
| - | - | - | - | - | - | ||
| - | - | - | - | - | |||
| - | - | - | - | ||||
| - | - | - | |||||
| - | - | ||||||
| - | |||||||
Найдем явную формулу для чисел S(n,k). Каждое разбиение M = E1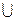 
E2 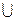... 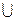Ek на непустые подмножества можно характеризовать набором чисел (l1, l2,....,ln), где
l1 — число подмножеств разбиения мощности 1,
l2 — число подмножеств разбиения мощности 2,
..........................................,
ln - число подмножеств разбиения мощности n.
Эти числа удовлетворяют тождеству
1 l1 + 2 l2 +.... + n ln = n.
Теорема 3.
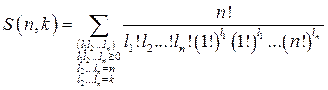
Доказательство.
Процесс построения всех разбиений множества M на k непустых частей, характеризуемых набором чисел (l1, l2,...., ln), l1 + l2 +.... + ln = k, можно представить следующим образом.
Возьмем п упорядоченных ячеек и разобьем их на k; подмножеств, характеризуемых данным набором чисел (l1, l2,...., ln). Эти подмножества занумеруем числами 0, 1,..., k - 1. Разместим в этих ячейках элементы а1,..., aп. Очевидно, что разбиение ячеек на подмножества структуры (l1, l2,...., ln) порождает разбиение элементов а1,..., aп на подмножества такой же структуры. Последнее задается набором (б1, б2,..., бп), где бi — номер подмножества разбиения ячеек, которому принадлежит элемент бi Производя различные размещения элементов а1,..., aп, по ячейкам, получим все разбиения множества M на k непустых частей данной структуры (l1, l2,...., ln). При этом два размещения определяют одно и то же разбиение множества M тогда и только тогда, когда для соответствующих им наборов (б1, б2,..., бп) и (б1, б2,..., бп) выполнено условие
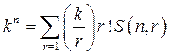
Если сравнить соответствующие слагаемые в (15) и (18), то можно увидеть, что они выражают одно и то же число. Отсюда получаем еще одно явное выражение для S(n,r) (n, r>0)
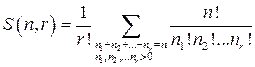
Эта формула не пригодна для практических вычислений S(n,k), так как она предполагает знание всех решений уравнения (14) или (17).
Эффективный способ вычисления чисел Стирлинга 2-го рода и изучение их свойств связано с установлением ряда реккурентных соотношений для S(n,k).
Теорема. S(m,n) = S(m-1,n-1) + n S(m-1,n)
Комбинаторные числа можно изучать двумя способами: теоретико-множественным и алгебраическим.
Числа Стирлинга 2-го рода (Джеймс Стирлинг (1699-1770))
Комбинаторные числа S(n,k) называются числа Стирлинга 2-го рода, а комбинаторные числа B(n) - числами Белла. Эти числа связаны соотношением:
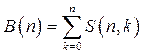
Число разбиений m -элементного множества на n блоков называется числом Стирлинга второго рода и обозначаются S(m,n)
Найдем явную формулу для определения чисел Стирлинга 2-го рода S(n,k).
По определению
S(m,0) = 0 при m > 0
S(m, m) = 1
S(0, 0) = 1
S(m,n) = 0 при n > m
Date: 2015-07-24; view: 1315; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |