
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Метод вариации произвольной постоянной.
В этом методе сначала решается соответствующее однородное линейное уравнение:  . Это уравнение с разделяющимися переменным, которое может быть записано в виде
. Это уравнение с разделяющимися переменным, которое может быть записано в виде  и проинтегрировано.
и проинтегрировано.
После интегрирования получим:

Под интегралом подразумевают любую первообразную.
На втором этапе решения считают, что с может зависеть от х. Отсюда происходит название: вариация произвольной постоянной. И решение уравнения  ищут в виде:
ищут в виде:  .
.
Подставим это значение у в дифференциальное уравнение:
 .
.
Второе и третье слагаемое в сумме равны нулю, т.к.  - это решение однородного дифференциального уравнения
- это решение однородного дифференциального уравнения  .
.
Для функции с получаем дифференциальное уравнение с разделяющимися переменными:  , решая которое находим функцию с, затем подставляем найденное с в выражение
, решая которое находим функцию с, затем подставляем найденное с в выражение  и получаем общее решение дифференциального уравнения.
и получаем общее решение дифференциального уравнения.
Пример:
Найти общее решение дифференциального уравнения:  .
.
1. найдем решение соответствующего однородного линейного дифференциального уравнения:
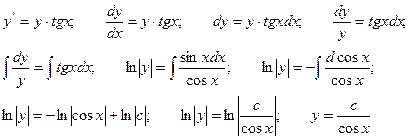 .
.
2. делаем произвольную постоянную зависимой от х, т.е. 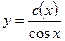 , и подставляем в исходное дифференциальное уравнение:
, и подставляем в исходное дифференциальное уравнение:


Подставляем найденное  в проект общего решения (
в проект общего решения (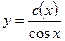 ) и получим:
) и получим: 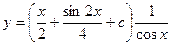 .
.
Метод Бернулли.
В этом методе решение уравнения  ищут в виде произведения двух функций
ищут в виде произведения двух функций  .
.
Суть метода в том, что одна из этих функций подбирается таким образом, чтобы для второй функции получалось уравнение с разделяющимися переменными.
 .
.

Функция Uвыбирается так, чтобы подчеркнутые слагаемые в сумме давали ноль. Чтобы найти такую функцию Uдостаточно решить уравнение:  . Это уравнение с разделяющимися переменными. Интегрируя его, находим функцию U(x). Произвольную постоянную можно взять любую.
. Это уравнение с разделяющимися переменными. Интегрируя его, находим функцию U(x). Произвольную постоянную можно взять любую.
Замечание: фактически для функции Uрешается соответствующее однородное уравнение.
Далее, в оставшуюся часть уравнения (*), подставляют найденную функцию U.  . Это уравнение с разделяющимися переменными для переменной V. Решая его находим V(x), а затем, перемножая UV, находим у.
. Это уравнение с разделяющимися переменными для переменной V. Решая его находим V(x), а затем, перемножая UV, находим у.
Пример: решим тот же пример методом Бернулли.
Найти общее решение дифференциального уравнения:  .
.
Ищем решение в виде  ;
;  .
.
Подставляем в дифференциальное уравнение:  .
.

1. выбираем Uтак, чтобы скобка обратилась в ноль, т.е. 
 . После интегрирования получим:
. После интегрирования получим:
 ; пусть с = 1
; пусть с = 1  .
.
2. подставим Uв уравнение (1):

3. перемножаем найденные Uи V:
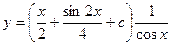 .
.
Date: 2016-07-18; view: 333; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |