Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами.

Определение: линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами будем называть дифференциальное уравнение вида: .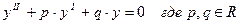

Будем искать частные решения этого уравнения в виде: , где k– некоторое число. Подставим это выражение в дифференциальное уравнение:

никогда не равно нулю, поэтому можно на него разделить.

Получим - это уравнение называется характеристическим; в зависимости от величины дискриминанта этого уравнения возможны три варианта решения исходного линейного дифференциального уравнения второго порядка:

1. характеристическое уравнение имеет два различных действительных корня: . В этом случае дифференциальное уравнение имеет два частных решения . Выше было показано, что эти функции линейно независимы, а, следовательно, общее решение дифференциального уравнения имеет вид: .

Пример: найти общее решение дифференциального уравнения: .

, общее решение: .

2. дискриминант характеристического уравнения равен нулю, следовательно характеристическое уравнение имеет два одинаковых корня: . В этом случае одно из решений дифференциального уравнения имеет вид , а второе линейно независимое решение уже не может иметь вид , поскольку . Будем искать второе линейно независимое решение в виде: .

Подставим это выражение в исходное дифференциальное уравнение:

Во всех слагаемых есть , вынесем его за скобки, а затем, в уравнении, сократим:

Интегрируем это уравнение и находим: .

Для нахождения частного решения можно взять любые значения А и В. чтобы новое частное решение получилось линейно независимым от первого возьмем А = 1, В = 0, следовательно U= х, следовательно .

В этом случае общее решение дифференциального уравнения имеет вид:

.

Пример: найти общее решение уравнения.

3. дискриминант характеристического уравнения отрицательный . В этом случае, характеристическое уравнения имеет два комплексно сопряженных корня (комплексно сопряженные числа отличаются только знаком перед мнимой частью) . В этом случае можно записать решение в виде: , где комплексные и подобраны так, чтобы общее решение получалось вещественным. Однако удобнее записывать общее решение в другой форме.

Утверждение: Если некоторая комплексная функция удовлетворяет дифференциальному уравнению , то этому дифференциальному уравнению будут удовлетворять по отдельности действительная часть и мнимая часть .

Доказательство:

- решение дифференциального уравнения.

Выпишем отдельно слагаемые с мнимой единицей и без нее:

Равенство нулю комплексного числа означает, что по отдельности равны нулю действительная и мнимая части, т.е.: .

А, поскольку , постольку, решениями дифференциального уравнения будут действительная и мнимая части.

Поэтому мы выберем: ,

тогда общее решение можно представить в виде: .

Пример: найти общее решение дифференциального уравнения.

Date: 2016-07-18; view: 313; Нарушение авторских прав