Проекционные методы решения краевых задач для обыкновенных дифференциальных уравнений

Краевыми задачами называются задачи, в которых дополнительные условия задаются при двух значениях независимой переменной (на концах рассматриваемого участка).

Рассмотрим краевую задачу на примере обыкновенного дифференциального уравнения второго порядка

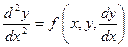
с граничными условиями

.

Сущность проекционных методов состоит в разложении решения по базису некоторых функций (проекций)

.

Базис 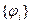выбирается в достаточной степени произвольно. В роли базисных функций могут выступать обычные полиномы , полиномы Лагранжа , Фурье-гармоники, наборы синусов и т.д.

Обязательные условия, которым должны удовлетворять базисные функции:

· разложение должно аппроксимировать ваше решение с любой, сколь угодно малой точностью (т.е. 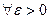существует такое 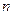, что норма отклонения );

· функции должны быть линейно независимы;

· любая комбинация функций должна удовлетворять поставленным граничным условиям.

После выбора базисных функций разложение подставляется в исходное уравнение, и получается система для расчета неизвестных коэффициентов .

Недостатки проекционных методов:

· произвольность в выборе базиса (характер полученного решения в определенной степени определяется характером базисных функций);

· необходимость решения больших систем алгебраических уравнений.

Преимущества:

· решение находится сразу во всей области изменения независимой переменной, а не в отдельных точках;

· погрешность расчета одинакова во всем диапазоне изменения независимой переменной (отсутствует экспоненциальный рост погрешности, характерный для методов решения задачи Коши).

Метод Галеркина

Метод Галеркина используется для приближенного решения краевых задач для дифференциальных уравнений, как обыкновенных, так и в частных производных.

Рассмотрим краевую задачу

(3.1)

Для ее приближенного решения выберем какую-либо последовательность базисных функций

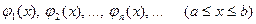(3.2)

т. е. последовательность функций, удовлетворяющих соответствующим однородным краевым условиям

и обладающих свойством полноты. Последнее означает, что любую функцию из достаточно широкого класса, удовлетворяющую указанным однородным краевым условиям, можно разложить в ряд по функциям (3.2).

Чаще всего полагают

или , .

Кроме того, надо выбрать какую-нибудь функцию , удовлетворяющую краевым условиям, указанным в (3.1), например,

или

Приближенное решение задачи (3.1) ищется в виде

, (3.3)

где функции , , … мы задаем, а постоянные , , 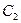…, подбираем. Тогда краевые условия, указанные в (3.1), заведомо удовлетворяются, а при подстановке выражения (3.3) в дифференциальное уравнение получается невязка (т. е. разность между левой и правой частями уравнения)

.

С ее помощью получаем систему из 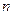уравнений с 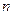неизвестными для определения

.

3.2. Реализация метода Галеркина в|посредством| MathCad

Пример. Найти методом Галеркина приближенное решение краевой задачи

, .

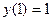Приведем решение краевой задачи с помощью|посредством| программного комплекса MathCad:

Сравним, значения точного и приближенного решений:

например, при имеем

Как видим, погрешность близка к 0,03 %. Для получения более точного решения необходимо использовать большее количество базисных функций.

Основные понятия метода конечных элементов

Метод конечных элементов (МКЭ) – это численная процедура решения задач, сформулированных в виде дифференциального уравнения или вариационного принципа. Метод конечных элементов отличается от классических методов Ритца и Галеркина тем, что аппроксимирующая функция является линейной комбинацией непрерывных кусочно-гладких финитных функций. Финитные функции отличны от нуля только в заданном интервале. В методе конечных элементов под такими интервалами подразумеваются конечные элементы, на которые разбивается область (область, на которой решается задача).

Термин метод конечных элементов, в действительности, определяет широкий спектр вычислительных технологий в соответствии с некоторыми общими свойствами.

Процесс конечно-элементного анализа включает определенную последовательность шагов. Перечислим эти шаги.

1. Дискретизация области: построение сетки, задание свойств элементов. Область, на которой решается задача, аппроксимируется (покрывается) непересекающимися подобластями простого типа, которые называются конечными элементами (КЭ). Множество элементов, на которые разбита область, называется конечно-элементной сеткой. Вершины КЭ называются узлами. Узлы предназначены для описания геометрии элемента и для задания компонент решения (неизвестная величина задается в узлах). Узлы могут быть внешними и внутренними. Внешние узлы лежат на границе КЭ и используются для соединения элементов друг с другом. Также узлы могут располагаться между угловыми узлами. КЭ может иметь и внутренние узлы, такие элементы обеспечивают более точное описание искомых функций. Компоненты решения в узле называются степенями свободы. В зависимости от рассматриваемых задач число степеней свободы в узле различно.

2. Выбор аппроксимирующих (базисных) функций. Чаще всего базисные функции выбираются в виде полиномов. Поэтому пространство, на котором ищется решение, является пространством кусочно-полиномиальных функций. Базисные функции могут иметь различный порядок: линейный, квадратичный, кубичный и т.д.

3. Формирование системы линейных алгебраических уравнений (СЛАУ) с учетом вкладов от элементов и узлов, введение граничных условий в систему уравнений.

4. Решение системы уравнений.

5. Определение расчетных величин в элементах. Этими величинами обычно являются производные от неизвестной функции (например, деформации, напряжения, скорости).

Точное решение дифференциального уравнения при подстановке в это дифференциальное уравнение обращает его в тождество в каждой точке. Решение МКЭ предполагает, что приближенное решение будет удовлетворять дифференциальному уравнению в узлах сетки .